No CrossRef data available.
Article contents
BOUNDING THE ORDER OF THE NILPOTENT RESIDUAL OF A FINITE GROUP
Published online by Cambridge University Press: 01 April 2016
Abstract
The last term of the lower central series of a finite group 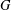 $G$ is called the nilpotent residual. It is usually denoted by
$G$ is called the nilpotent residual. It is usually denoted by 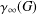 $\unicode[STIX]{x1D6FE}_{\infty }(G)$ . The lower Fitting series of
$\unicode[STIX]{x1D6FE}_{\infty }(G)$ . The lower Fitting series of 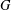 $G$ is defined by
$G$ is defined by 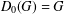 $D_{0}(G)=G$ and
$D_{0}(G)=G$ and 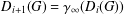 $D_{i+1}(G)=\unicode[STIX]{x1D6FE}_{\infty }(D_{i}(G))$ for
$D_{i+1}(G)=\unicode[STIX]{x1D6FE}_{\infty }(D_{i}(G))$ for 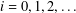 $i=0,1,2,\ldots \,$ . These subgroups are generated by so-called coprime commutators
$i=0,1,2,\ldots \,$ . These subgroups are generated by so-called coprime commutators 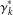 $\unicode[STIX]{x1D6FE}_{k}^{\ast }$ and
$\unicode[STIX]{x1D6FE}_{k}^{\ast }$ and 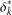 $\unicode[STIX]{x1D6FF}_{k}^{\ast }$ in elements of
$\unicode[STIX]{x1D6FF}_{k}^{\ast }$ in elements of 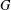 $G$ . More precisely, the set of coprime commutators
$G$ . More precisely, the set of coprime commutators 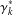 $\unicode[STIX]{x1D6FE}_{k}^{\ast }$ generates
$\unicode[STIX]{x1D6FE}_{k}^{\ast }$ generates 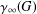 $\unicode[STIX]{x1D6FE}_{\infty }(G)$ whenever
$\unicode[STIX]{x1D6FE}_{\infty }(G)$ whenever 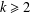 $k\geq 2$ while the set
$k\geq 2$ while the set 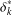 $\unicode[STIX]{x1D6FF}_{k}^{\ast }$ generates
$\unicode[STIX]{x1D6FF}_{k}^{\ast }$ generates 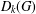 $D_{k}(G)$ for
$D_{k}(G)$ for 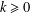 $k\geq 0$ . The main result of this article is the following theorem: let
$k\geq 0$ . The main result of this article is the following theorem: let 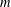 $m$ be a positive integer and
$m$ be a positive integer and 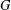 $G$ a finite group. Let
$G$ a finite group. Let 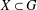 $X\subset G$ be either the set of all
$X\subset G$ be either the set of all 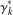 $\unicode[STIX]{x1D6FE}_{k}^{\ast }$ -commutators for some fixed
$\unicode[STIX]{x1D6FE}_{k}^{\ast }$ -commutators for some fixed 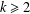 $k\geq 2$ or the set of all
$k\geq 2$ or the set of all 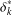 $\unicode[STIX]{x1D6FF}_{k}^{\ast }$ -commutators for some fixed
$\unicode[STIX]{x1D6FF}_{k}^{\ast }$ -commutators for some fixed 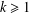 $k\geq 1$ . Suppose that the size of
$k\geq 1$ . Suppose that the size of 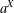 $a^{X}$ is at most
$a^{X}$ is at most 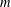 $m$ for any
$m$ for any 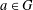 $a\in G$ . Then the order of
$a\in G$ . Then the order of 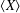 $\langle X\rangle$ is
$\langle X\rangle$ is 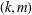 $(k,m)$ -bounded.
$(k,m)$ -bounded.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 273 - 277
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.

