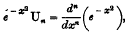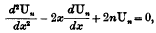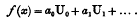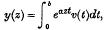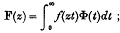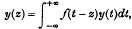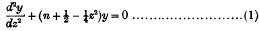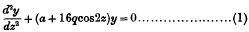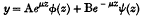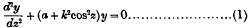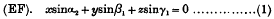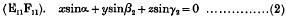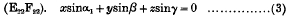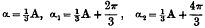Syllabus of papers
Thirty-Second Session, 1913–1914
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. v-vi
-
- Article
-
- You have access
- Export citation
Presents to the library
The following Presents to the Library have been received, for which the Society tenders its grateful thanks:–
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. vii-viii
-
- Article
-
- You have access
- Export citation
Office bearers
Office-Bearers
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 1
-
- Article
-
- You have access
- Export citation
Research Article
On the Equation of the Parabolic Cylinder Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 2-14
-
- Article
-
- You have access
- Export citation
Note on Gauss' Proof of the Reciprocity of Parallelism
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 15-18
-
- Article
-
- You have access
- Export citation
On some results concerning integral equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-29
-
- Article
-
- You have access
- Export citation
Notes on Spherical Harmonics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 30-35
-
- Article
-
- You have access
- Export citation
Some Graphical Methods for Determining Centres of Gravity
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 36-43
-
- Article
-
- You have access
- Export citation
Theorems analogous to Newton's Theorems on Symmetric Functions, with Elementary Proofs
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 44-48
-
- Article
-
- You have access
- Export citation
On Certain Formulae connected with the Function (cosnα – cosnθ)/(cosα – cosθ)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 49-57
-
- Article
-
- You have access
- Export citation
Concurrency of lines joining vertices of a triangle to opposite vertices of triangles on its sides
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 58-64
-
- Article
-
- You have access
- Export citation
On the continued fractions which represent the functions of Hermite and other functions defined by differential equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 65-74
-
- Article
-
- You have access
- Export citation
On the general solution of Mathieu's equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 75-80
-
- Article
-
- You have access
- Export citation
On the Quasi-periodic Solutions of Mathieu's Differential Equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 81-90
-
- Article
-
- You have access
- Export citation
On the Attractions of Spherical and Ellipsoidal Shells
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 91-100
-
- Article
-
- You have access
- Export citation
On certain theorems in Continued Fractions equivalent to Riemann's and other Transformations of the P-function
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 101-118
-
- Article
-
- You have access
- Export citation
The six trisectors of each of the angles of a triangle
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 119-131
-
- Article
-
- You have access
- Export citation
The Relation of Morley's Theorem to the Hessian Axis and Circumcentre
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 132-135
-
- Article
-
- You have access
- Export citation
Morley's Trisection Theorem: an Extension and its Relation to the Circles of Apollonius
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 136-150
-
- Article
-
- You have access
- Export citation
Other
John Sturgeon Mackay, M.A., LL.D.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 151-159
-
- Article
-
- You have access
- Export citation