Nature’s Sensors: Inferring the Invisible
Researchers use deflections of trees by wind to infer unknown wind speed.
The air that flows around us is invisible to the human eye, which makes direct observation of its motion and structure difficult. We can, however, feel its influence, through our skin and the deflection of our hair. At times, we can also see the interaction of air with other objects like the ripples formed on the surface of a body of water and the dancing of leaves on a tree. However, quantifying the movement of air is difficult. Flow-speed data can aid predictions of weather and the dispersion of pollutants, nutrients, and seeds. During emergencies, like the spread of wildfire, consequences can be mitigated by using wind-speed information to optimize evacuation plans and fire suppression strategies. Furthermore, accessing previously unknown speeds in remote areas would facilitate the optimal placement of wind turbines to boost energy harvesting.
Read this paper: Wind speed inference from environmental flow-structure interactions (Jennifer L. Cardona, Katherine L. Bouman and John O. Dabiri)
The problem is that high-resolution wind speed measurements are often difficult to ascertain. Pointwise measurements are straightforward to make using rotational anemometers, e.g. wind cups, and windsocks, which are commonly used at airstrips, are calibrated to provide an estimate of the wind velocity. Yet, these velocimeters often require deployment of the devices into the environment, affixing them to a structure. If environmental conditions are harsh, as in the midst of a wildfire, sensor deployment may not be possible or cause delay. Also, increased resolution typically requires increasing the number of sensors.
Researchers at Stanford University and California Institute of Technology have been developing an alternative anemometry approach: to infer wind speed U from the observed deflections ![]() of trees [1]. The advantages are clear: i) the ‘sensors’ are already deployed and ii) they are plentiful in many regions. If the method proves successful, a low-cost, high-volume, high-spatial-resolution visual anemometry is readily available anywhere trees are found. However, there are difficulties. First, the force exerted on an object by air, which subsequently generates a bending moment on the tree, is complicated, depending on the unknown flow state. Second, the deflection of the tree depends on its material and geometry. Measuring material properties for each individual tree is cumbersome and counter to the goals of developing a scalable anemometry technique.
of trees [1]. The advantages are clear: i) the ‘sensors’ are already deployed and ii) they are plentiful in many regions. If the method proves successful, a low-cost, high-volume, high-spatial-resolution visual anemometry is readily available anywhere trees are found. However, there are difficulties. First, the force exerted on an object by air, which subsequently generates a bending moment on the tree, is complicated, depending on the unknown flow state. Second, the deflection of the tree depends on its material and geometry. Measuring material properties for each individual tree is cumbersome and counter to the goals of developing a scalable anemometry technique.
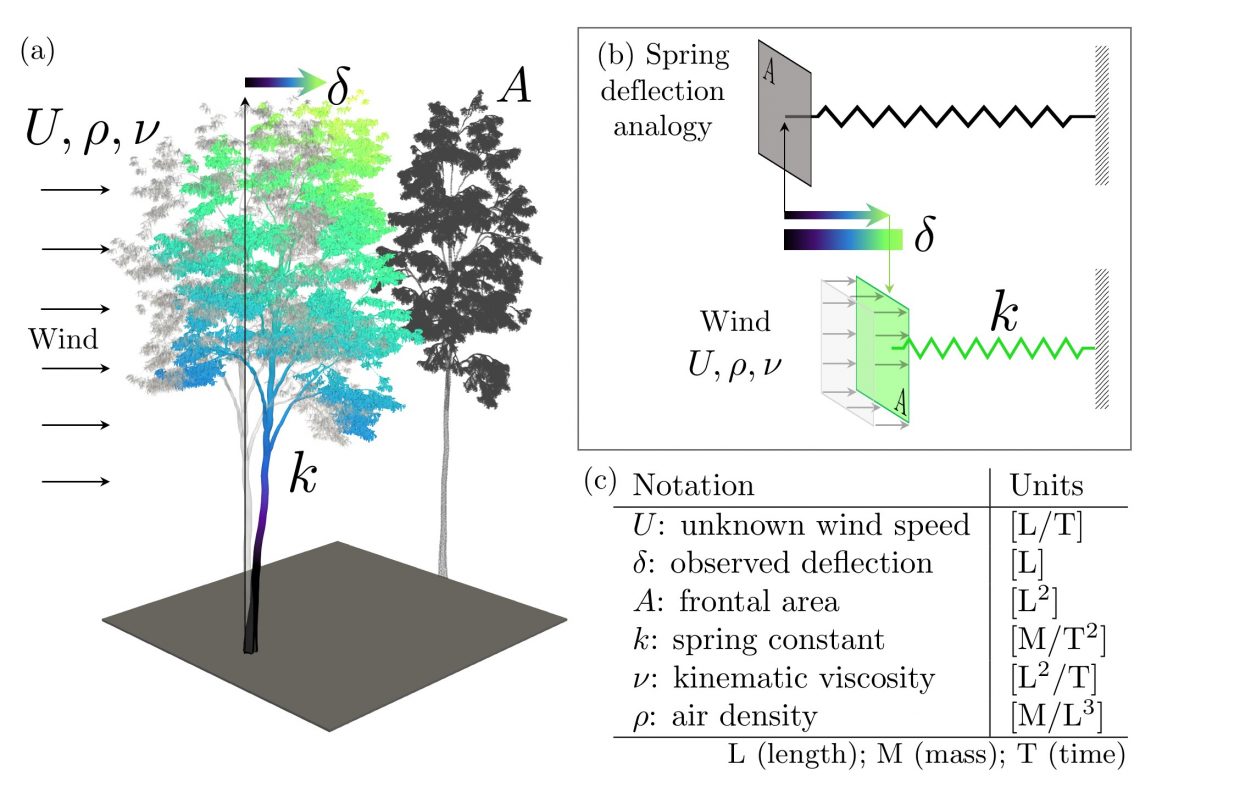
To mitigate some of these difficulties, the approach of Cardona et al. combines physics with a single deflection observation. The physical model is simple: the bending of the tree is analogous to the deflection of a spring by an applied force (see figure 1a and b for comparison of the configurations and list of parameters in c). Two forces are at play as shown in figure 2: i) the applied wind force and ii) the opposing spring force. By dimensional reasoning and some knowledge of fluid drag, the force exerted by the wind on a surface area A is proportional to the air density p times the velocity squared times the frontal area: ![]() Under steady-state conditions, the wind force is exactly balanced by the restoring force of the spring (or tree). Assuming a linear spring, the spring force is proportional to the observed deflection,
Under steady-state conditions, the wind force is exactly balanced by the restoring force of the spring (or tree). Assuming a linear spring, the spring force is proportional to the observed deflection, ![]() where the coefficient k depends on the material and geometry of the spring. To within an unknown constant, the physical model yields a direct relationship between the observed deflection and the unknown wind speed. Figure 2 summarizes the analysis and final expression.
where the coefficient k depends on the material and geometry of the spring. To within an unknown constant, the physical model yields a direct relationship between the observed deflection and the unknown wind speed. Figure 2 summarizes the analysis and final expression.

Without more information at this stage, the analysis would be stalled due to the unknown coefficient C. As Lord Rayleigh states [2], “…there is no prospect of determining a numerical coefficient from the principle of similarity alone; it must be found if at all, by further calculation, or experimentally.” To close the model, one additional measurement is needed. The unknown coefficient C, which is a combination of the spring and fluid drag coefficients, is found using an observation point: a deflection at a known input velocity. Afterward, the calibrated model can be used for the inverse problem: inferring wind speed from observed deflections.
So, how accurate are the model predictions? First, the group tested their approach on idealized cases, e.g., the bending of PVC pipes by wind. Tests were done in a well-characterized wind tunnel so that the predicted velocity could be validated against the true input velocity. The cylinder geometry provides additional simplifications: the frontal area perpendicular to the flow direction does not change, and the drag coefficient on a cylinder remains relatively constant for the wind speeds considered. For the control group of cantilevered cylinders, the errors in the predicted wind speed were less than 10% for wind speeds of 4.5 to 6.6 m/s.
With enhanced confidence in the model and embedded assumptions, the procedure was next applied to trees subjected to a uniform air flow. For a larger velocity range of 3.3 m/s to 11.4 m/s, fairly accurate estimates were obtained. Using a single reference velocity, the maximum error was less than 20%, without supplying knowledge of the material properties of the trees. Figure 3 shows how the predicted velocity, using the observation-infused model, correlates with the true wind-tunnel velocity.
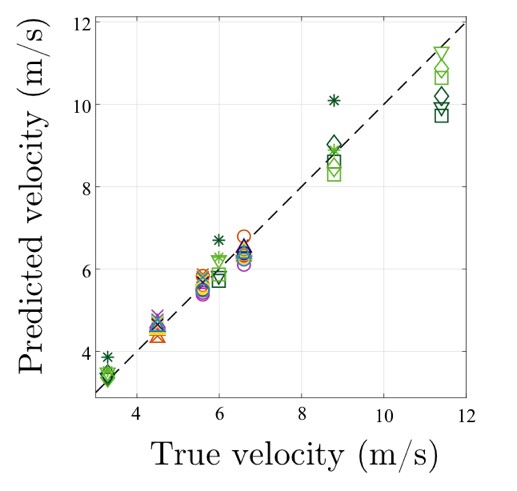
Ultimately, the approach of Cardona et al. [1] illustrates the merging of physics-based models with observations can enhance the prediction of uncertain quantities. Using only one observation point, the unknown parameters, like the strength of the tree, are sidestepped, enabling predictions. Efforts are currently ongoing to assess the performance of this technique when trying to infer wind speeds from field observations of tree oscillations in an atmospheric boundary-layer flow [3]. The authors hope to also be able to apply the method to other flow scenarios, including the measurement ocean currents from observations of the deflection of seagrass.
References
[2] Rayleigh. “The principles of similitude.” Nature. Volume 95, 66-68 (1915).






