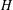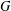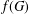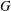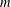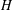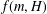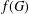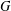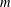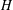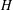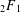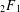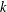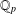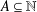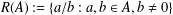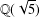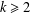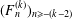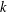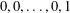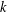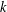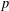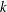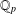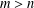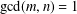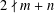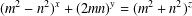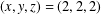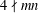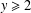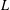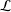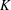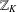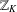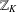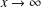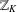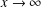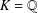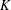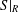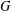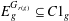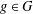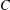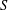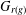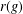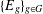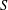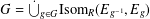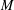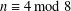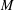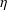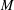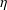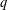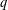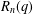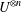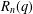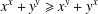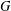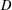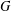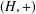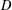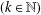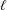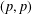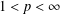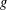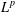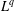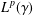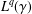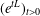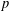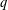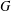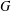Research Article
BIPARTITE SUBGRAPHS OF
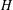 $H$-FREE GRAPHS
$H$-FREE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2017, pp. 1-13
-
- Article
-
- You have access
- Export citation
CONGRUENCES FOR TRUNCATED HYPERGEOMETRIC SERIES
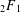 $_{2}F_{1}$
$_{2}F_{1}$
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2017, pp. 14-23
-
- Article
-
- You have access
- Export citation
THE QUOTIENT SET OF
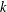 $k$-GENERALISED FIBONACCI NUMBERS IS DENSE IN
$k$-GENERALISED FIBONACCI NUMBERS IS DENSE IN 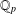 $\mathbb{Q}_{p}$
$\mathbb{Q}_{p}$
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 24-29
-
- Article
-
- You have access
- Export citation
JEŚMANOWICZ’ CONJECTURE ON PYTHAGOREAN TRIPLES
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 30-35
-
- Article
-
- You have access
- Export citation
ON ALGEBRAIC DIFFERENTIAL EQUATIONS FOR THE GAMMA FUNCTION AND
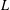 $L$-FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$-FUNCTIONS IN THE EXTENDED SELBERG CLASS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 36-43
-
- Article
-
- You have access
- Export citation
TWO PROBLEMS CONCERNING IRREDUCIBLE ELEMENTS IN RINGS OF INTEGERS OF NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, pp. 44-58
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION FOR A GROUPOID GALOIS EXTENSION USING PARTIAL ISOMORPHISMS
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2017, pp. 59-68
-
- Article
-
- You have access
- Export citation
A REMARK ON THE STABLE REAL FORMS OF COMPLEX VECTOR BUNDLES OVER MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 69-76
-
- Article
-
- You have access
- Export citation
THE ANNIHILATOR OF TENSOR SPACE IN THE
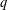 $q$-ROOK MONOID ALGEBRA
$q$-ROOK MONOID ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, pp. 77-86
-
- Article
-
- You have access
- Export citation
NEW ALGEBRAIC-TRIGONOMETRIC INEQUALITIES OF LAUB–ILANI TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, pp. 87-97
-
- Article
-
- You have access
- Export citation
MULTIPLE SOLUTIONS FOR A KIRCHHOFF EQUATION WITH NONLINEARITY HAVING ARBITRARY GROWTH
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 98-109
-
- Article
-
- You have access
- Export citation
ON EXTENSIONS OF THE GENERALISED JENSEN FUNCTIONS ON SEMIGROUPS
-
- Published online by Cambridge University Press:
- 13 February 2017, pp. 110-116
-
- Article
-
- You have access
- Export citation
ON INTEGRAL ESTIMATES OF NONNEGATIVE POSITIVE DEFINITE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 117-125
-
- Article
-
- You have access
- Export citation
ON LITTLEWOOD–PALEY FUNCTIONS ASSOCIATED WITH THE DUNKL OPERATOR
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 126-138
-
- Article
-
- You have access
- Export citation
COMPATIBLE LOCALLY CONVEX TOPOLOGIES ON NORMED SPACES: CARDINALITY ASPECTS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 139-145
-
- Article
-
- You have access
- Export citation
ON MULTIPLIERS BETWEEN SOME SPACES OF HOLOMORPHIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 146-153
-
- Article
-
- You have access
- Export citation
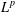 $L^{p}$–
$L^{p}$–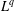 $L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS
$L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 154-161
-
- Article
-
- You have access
- Export citation
ON THE CONVERGENCE RATE OF THE KRASNOSEL’SKIĬ–MANN ITERATION
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2017, pp. 162-170
-
- Article
-
- You have access
- Open access
- Export citation
ON KILLERS OF CABLE KNOT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 171-176
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
BAZ volume 96 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 July 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation