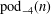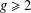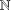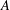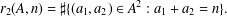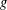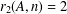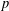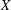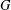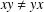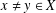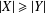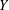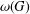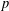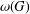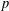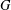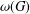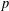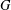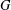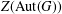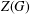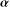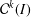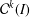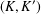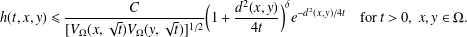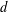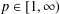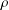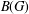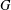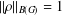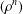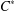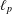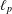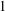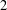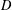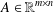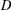Research Article
ARITHMETIC PROPERTIES OF PARTITION QUADRUPLES WITH ODD PARTS DISTINCT
- Part of:
-
- Published online by Cambridge University Press:
- 08 July 2015, pp. 353-364
-
- Article
-
- You have access
- Export citation
A FORMULA FOR THE NUMBER OF SPANNING TREES IN CIRCULANT GRAPHS WITH NONFIXED GENERATORS AND DISCRETE TORI
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2015, pp. 365-373
-
- Article
-
- You have access
- Export citation
ON MINIMAL ASYMPTOTIC
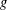 $g$-ADIC BASES
$g$-ADIC BASES
- Part of:
-
- Published online by Cambridge University Press:
- 05 August 2015, pp. 374-379
-
- Article
-
- You have access
- Export citation
ON MAXIMAL SUBSETS OF PAIRWISE NONCOMMUTING ELEMENTS IN FINITE
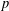 $p$-GROUPS
$p$-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 20 August 2015, pp. 380-389
-
- Article
-
- You have access
- Export citation
ON THE CENTRE OF THE AUTOMORPHISM GROUP OF A GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2015, pp. 390-396
-
- Article
-
- You have access
- Export citation
A SHARP VERSION OF BONSALL’S INEQUALITY
- Part of:
-
- Published online by Cambridge University Press:
- 19 August 2015, pp. 397-404
-
- Article
-
- You have access
- Export citation
FRACTAL BASES FOR BANACH SPACES OF SMOOTH FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 30 July 2015, pp. 405-419
-
- Article
-
- You have access
- Export citation
QUASICONFORMAL SOLUTIONS OF POISSON EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 August 2015, pp. 420-428
-
- Article
-
- You have access
- Export citation
OBSERVATIONS ON GAUSSIAN UPPER BOUNDS FOR NEUMANN HEAT KERNELS
- Part of:
-
- Published online by Cambridge University Press:
- 08 July 2015, pp. 429-439
-
- Article
-
- You have access
- Export citation
ON ITERATED POWERS OF POSITIVE DEFINITE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2015, pp. 440-443
-
- Article
-
- You have access
- Export citation
STABILITY OF UNCONDITIONAL SCHAUDER DECOMPOSITIONS IN
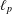 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 03 August 2015, pp. 444-456
-
- Article
-
- You have access
- Export citation
A WEAKLY UNIFORMLY ROTUND DUAL OF A BANACH SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 10 August 2015, pp. 457-462
-
- Article
-
- You have access
- Export citation
UNIFORMLY BOUNDED COMPOSITION OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 30 July 2015, pp. 463-469
-
- Article
-
- You have access
- Export citation
RESOLVABILITY PROPERTIES OF SIMILAR TOPOLOGIES
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2015, pp. 470-477
-
- Article
-
- You have access
- Export citation
ON ALGEBRAIC INVARIANTS FOR FREE ACTIONS ON HOMOTOPY SPHERES
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2015, pp. 478-487
-
- Article
-
- You have access
- Export citation
DETERMINING THE NUCLEOLUS OF COMPROMISE STABLE GAMES
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2015, pp. 488-495
-
- Article
-
- You have access
- Export citation
THE RESTRICTED ISOMETRY PROPERTY FOR SIGNAL RECOVERY WITH COHERENT TIGHT FRAMES
- Part of:
-
- Published online by Cambridge University Press:
- 19 August 2015, pp. 496-507
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
QUASI RIESZ TRANSFORMS, HARDY SPACES AND GENERALISED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
- Part of:
-
- Published online by Cambridge University Press:
- 10 August 2015, pp. 508-510
-
- Article
-
- You have access
- Export citation
DIMENSIONAL CHARACTERISTICS OF THE NONWANDERING SETS OF OPEN BILLIARDS
- Part of:
-
- Published online by Cambridge University Press:
- 11 August 2015, pp. 511-513
-
- Article
-
- You have access
- Export citation
NONLINEAR ANALYSIS IN GEODESIC METRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 05 August 2015, pp. 514-515
-
- Article
-
- You have access
- Export citation