Hostname: page-component-6bb9c88b65-dwch4 Total loading time: 0 Render date: 2025-07-21T16:45:09.193Z Has data issue: false hasContentIssue false
  • English
  • Français

FRACTAL BASES FOR BANACH SPACES OF SMOOTH FUNCTIONS

Part of: Classical measure theory Normed linear spaces and Banach spaces; Banach lattices Approximations and expansions

Published online by Cambridge University Press:  30 July 2015

M. A. NAVASCUÉS ,
P. VISWANATHAN ,
A. K. B. CHAND ,
M. V. SEBASTIÁN  and
S. K. KATIYAR
M. A. NAVASCUÉS
Affiliation:
Departmento de Matemática Aplicada, Escuela de Ingeniería y Arquitectura, Universidad de Zaragoza, C/- María de Luna 3, Zaragoza 50018, Spain email manavas@unizar.es
P. VISWANATHAN*
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, Australia email amritaviswa@gmail.com
A. K. B. CHAND
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai, India email chand@iitm.ac.in
M. V. SEBASTIÁN
Affiliation:
Centro Universitario de la Defensa de Zaragoza, Academia General Militar, Zaragoza, Spain email msebasti@unizar.es
S. K. KATIYAR
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai, India email sbhkatiyar@gmail.com
*
✉amritaviswa@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This article explores the properties of fractal interpolation functions with variable scaling parameters, in the context of smooth fractal functions. The first part extends the Barnsley–Harrington theorem for differentiability of fractal functions and the fractal analogue of Hermite interpolation to the present setting. The general result is applied on a special class of iterated function systems in order to develop differentiability of the so-called 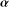$\boldsymbol{{\it\alpha}}$-fractal functions. This leads to a bounded linear map on the space 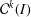${\mathcal{C}}^{k}(I)$ which is exploited to prove the existence of a Schauder basis for 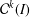${\mathcal{C}}^{k}(I)$ consisting of smooth fractal functions.

Keywords

smooth fractal functionHermite fractal interpolation functionfractal operatortopological isomorphismSchauder basisMarkushevich basis

MSC classification

Primary: 28A80: Fractals
Secondary: 41A05: Interpolation 46B15: Summability and bases

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 3 , December 2015 , pp. 405 - 419
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Barnsley, M. F., ‘Fractal functions and interpolation’, Constr. Approx. 2(1) (1986), 303–329.CrossRefGoogle Scholar
Barnsley, M. F., Fractals Everywhere (Academic Press, San Diego, 1988).Google Scholar
Barnsley, M. F. and Harrington, A. N., ‘The calculus of fractal interpolation functions’, J. Approx. Theory 57(1) (1989), 14–34.CrossRefGoogle Scholar
Chand, A. K. B. and Viswanathan, P., ‘A constructive approach to cubic Hermite fractal interpolation function and its constrained aspects’, BIT 53(4) (2013), 841–865.CrossRefGoogle Scholar
Cheney, E. W., Approximation Theory (AMS Chelsea Publishing Company, Providence, RI, 1966).Google Scholar
Conway, J. B., A Course in Functional Analysis, 2nd edn (Springer, New York, 1996).Google Scholar
Navascués, M. A., ‘Fractal polynomial interpolation’, Z. Anal. Anwend. 24(2) (2005), 1–20.Google Scholar
Navascués, M. A., ‘Fractal approximation’, Complex Anal. Oper. Theory 4(4) (2010), 953–974.CrossRefGoogle Scholar
Navascués, M. A., ‘Fractal bases of L p spaces’, Fractals 20 (2012), 141–148.CrossRefGoogle Scholar
Navascués, M. A., ‘Affine fractal functions as bases of continuous functions’, Quaest. Math. 37 (2014), 1–14.CrossRefGoogle Scholar
Navascués, M. A. and Sebastián, M. V., ‘Generalization of Hermite functions by fractal interpolation’, J. Approx. Theory 131(1) (2004), 19–29.CrossRefGoogle Scholar
Navascués, M. A. and Sebastián, M. V., ‘Fitting curves by fractal interpolation: an application to electroencephalographic processing’, in: Thinking in Patterns: Fractals and Related Phenomena in Nature (ed. Novak, M. M.) (World Scientific Publishing, Singapore City, 2004), 143–154.CrossRefGoogle Scholar
Navascués, M. A. and Sebastián, M. V., ‘Smooth fractal interpolation’, J. Inequal. Appl. 2006(78734) (2006), 1–20.CrossRefGoogle Scholar
Schonefeld, S., ‘Schauder bases in spaces of differentiable functions’, Bull. Amer. Math. Soc. (N.S.) 75 (1969), 586–590.CrossRefGoogle Scholar
Stoer, J. and Bulirsch, R., Introduction to Numerical Analysis (Springer, NewYork, 1980).CrossRefGoogle Scholar
Viswanathan, P. and Chand, A. K. B., ‘Fractal rational functions and their approximation properties’, J. Approx. Theory 185 (2014), 31–50.CrossRefGoogle Scholar
Viswanathan, P., Chand, A. K. B. and Navascués, M.A., ‘Fractal perturbation preserving fundamental shapes: bounds on the scale factors’, J. Math. Anal. Appl. 419(2) (2014), 804–817.CrossRefGoogle Scholar
Wang, H. Y. and Yu, J. S., ‘Fractal interpolation functions with variable parameters and their analytical properties’, J. Approx. Theory 175 (2013), 1–18.CrossRefGoogle Scholar