Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-31T20:42:29.524Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MAXIMAL SUBSETS OF PAIRWISE NONCOMMUTING ELEMENTS IN FINITE 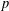$p$-GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  20 August 2015

M. R. DARAFSHEH ,
M. GHORBANI  and
S. K. PRAJAPATI
M. R. DARAFSHEH*
Affiliation:
School of Mathematics, Statistics, and Computer Science, College of Science, University of Tehran, Tehran, Iran email darafsheh@ut.ac.ir
M. GHORBANI
Affiliation:
Department of Mathematics, Mazandaran University of Science and Technology, P.O. Box 11111, Behshahr, Iran email m_ghorbani@iust.ac.ir
S. K. PRAJAPATI
Affiliation:
Einstein Institute of Mathematics, Hebrew University of Jerusalem, Jerusalem 91904, Israel email skprajapati.iitd@gmail.com
*
✉darafsheh@ut.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subset 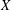$X$ of a finite group 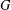$G$ is a set of pairwise noncommuting elements if 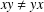$xy\neq yx$ for all 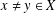$x\neq y\in X$. If 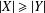$|X|\geq |Y|$ for any other subset 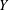$Y$ of pairwise noncommuting elements, then 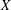$X$ is called a maximal subset of pairwise noncommuting elements and the size of such a set is denoted by 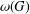${\it\omega}(G)$. In a recent article by Azad et al. [‘Maximal subsets of pairwise noncommuting elements of some finite 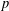$p$-groups’, Bull. Iran. Math. Soc.39(1) (2013), 187–192], the value of 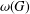${\it\omega}(G)$ is computed for certain 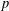$p$-groups 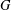$G$. In the present paper, our aim is to generalise these results and find 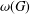${\it\omega}(G)$ for some more 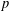$p$-groups of interest.

Keywords

pairwise noncommuting elementsAC-groupsfinite p-groups

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Secondary: 20D15: Nilpotent groups, $p$-groups

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 3 , December 2015 , pp. 380 - 389
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Abdollahi, A., Akbari, A. and Maimani, H. R., ‘Non-commuting graph of a group’, J. Algebra 298 (2006), 468–492.CrossRefGoogle Scholar
Anilkumar, C. P. and Prasad, A., ‘Orbits of pairs in abelian groups’, Sém. Lothar. Combin. 70 (2014), art. B70h.Google Scholar
Azad, A., Fouladi, S. and Orfi, R., ‘Maximal subsets of pairwise non-commuting elements of some finite p-groups’, Bull. Iranian Math. Soc. 39(1) (2013), 187–192.Google Scholar
Bertram, E. A., ‘Some applications of graph theory to finite groups’, Discrete Math. 44 (1983), 31–43.CrossRefGoogle Scholar
Chin, A. Y. M., ‘On non-commuting sets in an extraspecial p-group’, J. Group Theory 8(2) (2005), 189–194.CrossRefGoogle Scholar
Fouladi, S. and Orfi, R., ‘Maximal Subsets of pairwise noncommuting elements of some p-groups of maximal class’, Bull. Aust. Math. Soc. 84 (2011), 447–451.CrossRefGoogle Scholar
Fouladi, S. and Orfi, R., ‘Maximum size of subsets of pairwise non-commuting elements in finite metacyclic p-groups’, Bull. Aust. Math. Soc. 87 (2013), 18–23.CrossRefGoogle Scholar
James, R., ‘The groups of order p 6 (p an odd prime)’, Math. Comp. 34(150) (1980), 613–637.Google Scholar
Mason, D. R., ‘On coverings of a finite group by abelian subgroups’, Math. Proc. Cambridge Philos. Soc. 83(2) (1978), 205–209.CrossRefGoogle Scholar
Neumann, B. H., ‘A problem of Paul Erdos on groups’, J. Aust. Math. Soc. 21 (1976), 467–472.CrossRefGoogle Scholar
Orfi, R., ‘Maximal Subsets of pairwise non-commuting elements of p-groups of order less than p 6’, Int. J. Group Theory 3(1) (2014), 65–72.Google Scholar
Pyber, L., ‘The number of pairwise non-commuting elements and the index of the center in a finite group’, J. Lond. Math. Soc. (2) 35(2) (1987), 287–295.CrossRefGoogle Scholar
Robinson, D. J. S., A Course in the Theory of Groups (Springer, New York, 1982).CrossRefGoogle Scholar
Rocke, D. M., ‘p-groups with abelian centralizers’, Proc. Lond. Math. Soc. (3) 30(3) (1975), 55–75.CrossRefGoogle Scholar
Serre, J. P., ‘Sur la dimension cohomologique des groups profinis’, Topology 3 (1965), 413–420.CrossRefGoogle Scholar