No CrossRef data available.
Article contents
ON ITERATED POWERS OF POSITIVE DEFINITE FUNCTIONS
Published online by Cambridge University Press: 16 June 2015
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We prove that if 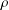 ${\it\rho}$ is an irreducible positive definite function in the Fourier–Stieltjes algebra
${\it\rho}$ is an irreducible positive definite function in the Fourier–Stieltjes algebra 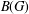 $B(G)$ of a locally compact group
$B(G)$ of a locally compact group 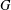 $G$ with
$G$ with 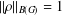 $\Vert {\it\rho}\Vert _{B(G)}=1$, then the iterated powers
$\Vert {\it\rho}\Vert _{B(G)}=1$, then the iterated powers 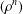 $({\it\rho}^{n})$ as a sequence of unital completely positive maps on the group
$({\it\rho}^{n})$ as a sequence of unital completely positive maps on the group 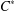 $C^{\ast }$-algebra converge to zero in the strong operator topology.
$C^{\ast }$-algebra converge to zero in the strong operator topology.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 92 , Issue 3 , December 2015 , pp. 440 - 443
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
Biane, Ph., ‘Quantum random walk on the dual of SU (n)’, Probab. Theory Related Fields 89 (1991), 117–129.CrossRefGoogle Scholar
Chu, C.-H. and Lau, A. T.-M., Harmonic Functions on Groups and Fourier Algebras, Lecture Notes in Mathematics, 1782 (Springer, Berlin, 2002).CrossRefGoogle Scholar
Derriennic, Y., ‘Lois “zéro ou deux” pour les processus de Markov. Applications aux marches aléatoires’, Ann. Inst. H. Poincaré B (N.S.) 12(2) (1976), 111–129.Google Scholar
Eymard, P., ‘L’algèbra de Fourier d’un groupe localement compact’, Bull. Soc. Math. France 92 (1964), 181–236.CrossRefGoogle Scholar
Hofmann, K. H. and Mukherjea, A., ‘Concentration functions and a class of noncompact groups’, Math. Ann. 256(4) (1981), 535–548.CrossRefGoogle Scholar
Izumi, M., ‘Non-commutative Poisson boundaries and compact quantum group actions’, Adv. Math. 169(1) (2002), 1–57.CrossRefGoogle Scholar
Jaworski, W., Rosenblatt, J. and Willis, G., ‘Concentration functions in locally compact groups’, Math. Ann. 305(4) (1996), 673–691.CrossRefGoogle Scholar
Kalantar, M., ‘A limit theorem for discrete quantum groups’, J. Funct. Anal. 265(3) (2013), 469–473.CrossRefGoogle Scholar
Kalantar, M., Neufang, M. and Ruan, Z.-J., ‘Poisson boundaries over locally compact quantum groups’, Internat. J. Math. 24(3) (2013), 1350023.CrossRefGoogle Scholar
Mukherjea, A., ‘Limit theorems for probability measures on non-compact groups and semi-groups’, Z. Wahrscheinlichkeitsth. verw. Geb. 33(4) (1976), 273–284.CrossRefGoogle Scholar
Neufang, M. and Runde, V., ‘Harmonic operators: the dual perspective’, Math. Z. 255 (2007), 669–690.CrossRefGoogle Scholar

