Magnetic fields are at the core of many imaging technologies. A widely known modality is MRI, a standard procedure in medical imaging, which is however limited by a long scanning time and the ability to only image anatomical regions containing sufficient amounts of water. The more recent magnetic particle imaging (MPI) instead promises functional images of the dynamics of nanoparticle tracers with high temporal resolution – scanning times are typically in the sub-second regime. As precision and scalability of these technologies improve, so does the need for efficient mathematical descriptions of the magnetic fields involved. A new study in the European Journal of Applied Mathematics (EJAM) by Marija Boberg, Tobias Knopp, and Martin Möddel — researchers based in Hamburg, where MPI was originally invented and continues to be actively developed — proposes a novel framework for uniquely and compactly representing magnetic fields using truncated real solid harmonic expansions.

Magnetic fields in MPI are quasi-static, satisfying Laplace’s equation in regions free of electric current. This allows the field to be decomposed into real solid spherical harmonics functions, which generalize solutions to Laplace’s equation on spherical domains. Each magnetic field component is expanded separately, with coefficients encoding constant, linear, and higher-order variations of the field.

A standard challenge in applying spherical harmonic expansions is that the expansion coefficients depend on the geometry of the measurement setup, specifically, on the center and radius of the measurement sphere. This dependency complicates comparisons across different measurements, especially in MPI, where the imaging domain is often stitched together from overlapping patches, each sampled under slightly different conditions.

To address this, the authors of the new paper “Unique compact representation of magnetic fields using truncated solid harmonic expansions”, published in EJAM, introduce a method to shift the expansion point of a solid harmonic expansion by translating the coefficients themselves — a result derived from adapting classical addition theorems for spherical harmonics. This enables a unique representation of the field at any chosen point, independent of the measurement geometry. In MPI applications, they use the field-free-point (FFP) of the selection field as a natural and scanner-specific expansion center.

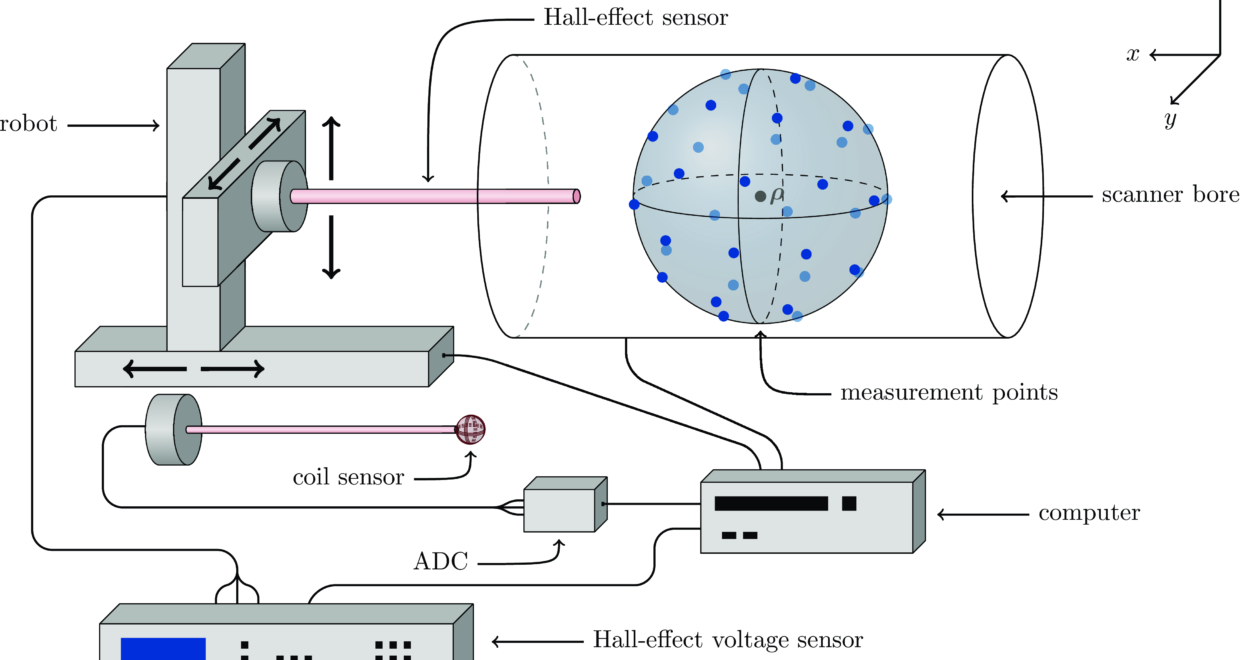
To compute the coefficients efficiently, the authors recommend spherical t-designs: special point configurations on the sphere that yield exact quadrature for polynomials up to a given degree. Compared to Gauss–Legendre quadrature rules, t-designs require fewer points, significantly reducing measurement time without sacrificing accuracy.

The theoretical framework is complemented by a detailed application to a real MPI system. Magnetic fields were measured using a 3-axis Hall-effect sensor at the nodes of a spherical 8-design inside the scanner bore. These measurements, when translated into the FFP frame using the proposed coefficient shift method, yield field representations that can be directly compared across patches.

The approach also enables the detection and quantification of field imperfections. In ideal MPI conditions, only constant and linear field terms should be nonzero. Deviations in higher-order terms or orthogonal components signal measurement errors or local imperfections in the magnetic field — critical information for improving image quality or calibrating the system.

Beyond the theoretical derivation and numerical validation, the work stands out by offering an open-source implementation of the full pipeline, packaged in a Julia library. This includes routines for computing expansions, translating coefficients, and evaluating the resulting fields numerically. While the paper focuses on MPI, the mathematical tools are broadly applicable to any context where magnetic fields satisfy Laplace’s equation, for instance, MRI shimming or geophysical magnetometry. The combination of mathematical rigor and practical implementation makes this a compelling contribution to applied harmonic analysis and imaging science.

The paper ‘Unique compact representation of magnetic fields using truncated solid harmonic expansions‘ by Marija Boberg, Tobias Knopp and Martin Möddel appears in European Journal of Applied Mathematics and is available open access.

Since 2008 EJAM surveys have been expanded to cover Applied and Industrial Mathematics. Coverage of the journal has been strengthened in probabilistic applications, while still focusing on those areas of applied mathematics inspired by real-world applications, and at the same time fostering the development of theoretical methods with a broad range of applicability.

Survey papers contain reviews of emerging areas of mathematics, either in core areas or with relevance to users in industry and other disciplines. Research papers may be in any area of applied mathematics. A special emphasis is on new mathematical ideas, relevant to modelling and analysis in modern science and technology, and the development of interesting mathematical methods of wide applicability.