To be eligible for the 2017 Mahony-Neumann-Room Prize, papers must have been published in the Bulletin of the Australian Mathematical Society during the period 2011-2016 (volumes 83-94).

The initial list of candidates came from two sources. Cambridge University Press provided a list of the most highly cited papers published during the period 2011-2016. I supplemented this with a list of papers published during the period 2014-2016 which had at least one citation and were most highly regarded by the referees. The rationale for these two approaches is that the more recent papers have not had much time to amass citations but had at least attracted some attention. Altogether, this produced a list of 29 papers.

The papers cover a wide variety of fields and styles and are not easy to compare. However, a clear pattern emerged after consultation with the Associate Editors.

On this basis, I proposed a shortlist of six papers for further consideration by the Prize Committee. For each paper, I have provided a short synopsis from the abstract of the paper and a summary of the comments made by the referee and the Associate Editors. The papers are listed in order of publication.

Read more about the Mahony-Neumann-Room Prize.

Shortlisted papers

D.W. Barnes
On Levi’s Theorem for Leibniz Algebras
Vol 86(2) (2012), 184-185

67 citations (none by the author), including 27 citations in 2016 and 2017

A Lie algebra over a field of characteristic 0 splits over its soluble radical and all complements are conjugate. It is shown in this paper that the splitting theorem extends to Leibniz algebras but that the conjugacy theorem does not.

The impressive citation count confirms the importance of the result for the study of Leibniz algebras. The proof is short, concise and clear and relies on two results from Jacobson’s Lie Algebras. Recent citations seem to acknowledge the place of the paper in the development of the subject.

Janusz Brzdek
A Hyperstability Result for the Cauchy Equation
Vol 89(1) (2014), 33-40

28 citations, including 11 citations in 2016 and 2017

The paper proves a hyperstability result for the Cauchy functional equation f (x + y) = f (x) + f (y), which complements some earlier stability outcomes of J. M. Rassias. It gives a new method for proving stability for functional equations, based on a fixed point theorem.

The methods introduced here, while not entirely novel, have been made widely applicable and have already influenced others working in this field. Similar results have been obtained for other functional equations and more general settings. The exposition is excellent.

Allan P. Donsig, David Milan
Joins and covers in inverse semigroups and tight C*-algebras
Vol 90(1) (2014), 121-133

3 citations

The paper shows Exel’s tight representation of an inverse semigroup can be described in terms of joins and covers in the natural partial order. This result is used to show that the C⇤-algebra of a finitely aligned category of paths, developed by Spielberg, is the tight C⇤-algebra of a natural inverse semigroup. This includes as a special case finitely aligned higher-rank graphs.

The paper is very well written and links various constructions of C*-algebras from semigroups and other combinatorial objects. Moreover, it links these various constructions in a way which sheds new light on all of them. The paper has a very nice and helpful introduction before presenting a very nice set of results. The methods are novel and the generality of the results is impressive. They are significant.

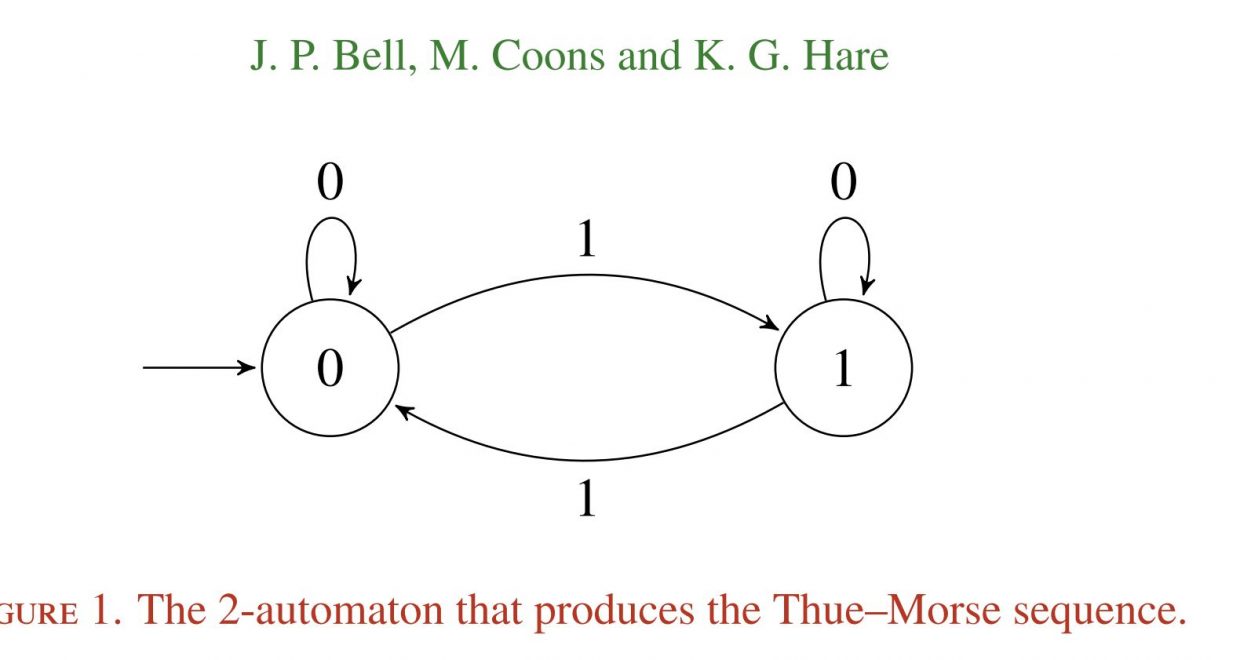
Jason P. Bell, Michael Coons and Kevin G. Hare
The minimal growth of a k-regular sequence
Vol 90(2) (2014), 195-203

11 citations including 7 in 2016 and 2017

The paper gives a lower bound for the growth of an unbounded Z-valued k-regular sequence. The ideas are applied to answer a question of Borwein, Choi and Coons on the sums of completely multiplicative automatic functions. There is a connection with a famous problem of Erdos in this area.

The paper attacks a concrete and nontrivial problem and gives a very comprehensive solution, including both an asymptotic lower bound and examples to demonstrate that this estimate is best possible. The paper sheds light on important conjectures about automatic sequences. The exposition is excellent.

This paper was announced as the winner of the 2017 Mahony-Neumann-Room Prize during the opening session of the Australian Mathematical Society Annual Conference at Macquarie University in December.

Timothy C. Burness and Elisa Covato
On the prime graph of simple groups
Vol 91(2) (2015), 227-240

3 citations

Let G be a finite group, let $\pi(G)$ be the set of prime divisors of |G| and let $\Gamma(G)$ be the prime graph of G. This graph has vertex set $\pi(G)$ and two vertices r and s are adjacent if and only if G contains an element of order rs. Many properties of these graphs have been studied in recent years, with a particular focus on the prime graphs of finite simple groups. The paper determines the pairs (G, H), where G is simple and H is a proper subgroup of G such that $\Gamma(G) = \Gamm(H)$.

The paper is well written and well motivated.  It gives comprehensive results on a concrete question and some context for future work including a description of barriers to progress.

Masanobu Kaneko and Mika Sakata
On multiple zeta values of extremal height
Vol 93(2) (2016), 186-193

2 citations

The paper gives three identities involving multiple zeta values of height one and of maximal height: an explicit formula for the height one multiple zeta values, a regularised sum formula and a sum formula for the multiple zeta values of maximal height.

These are beautiful and well-motivated results, very nicely presented and likely of broad interest. There is good discussion of connections with the literature.

All papers are free to read for the duration of 2018.