References
Alexander, J. W. (1928). Topological invariants of knots and links. Transactions of the American Mathematical Society, 30(2):275–306.
Alexander, J. W. and Briggs, G. B. (1926). On types of knotted curves. Annals of Mathematics, 28(1/2):562–586.
Allwein, G. and Barwise, J., editors (1996). Logical Reasoning with Diagrams. Oxford University Press, Oxford.
Avron, A. (1988). The semantics and proof theory of linear logic. Theoretical Computer Science, 57:161–184.
Babbage, C. (1830). On notations. Edinburgh Encyclopedia, 15:394–399.
Bauer, F. L. (2002). From the stack principle to ALGOL. In Broy, M. and Denert, E., editors, Software Pioneers, pages 26–42. Springer, New York.
Bellucci, F., Moktefi, A., and Pietarinen, A.-V. (2018). Simplex sigillum veri: Peano, Frege, and Peirce on the primitives of logic. History and Philosophy of Logic, 39(1):80–95.
Blanchette, P. (2012). Frege’s Conception of Logic. Oxford University Press, Oxford.
Boole, G. (1854). An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities. Walton and Maberly, London.
Bos, H. J. M. (2001). Redefining Geometrical Exactness: Descartes’ Transformation of the Early Modern Concept of Construction. Springer, New York.
Brown, J. R. (2008). Philosophy of Mathematics: A Contemporary Introduction to the World of Proofs and Pictures. Routledge, New York, 2nd edition.
Cajori, F. (1925). Leibniz, the master-builder of mathematical notations. Isis, 7(3):412–429.
Cajori, F. (1928a). A History of Mathematical Notations, volume I: Notations in Elementary Mathematics. Open Court Publishing Company, Chicago.
Cajori, F. (1928b). Uniformity of mathematical notations: Retrospect and prospect. In Fields, J. C., editor, Proceedings of the International Congress of Mathematicians, Toronto, August 11–16, 1924, volume 2, pages 924–936, University of Toronto Press, Toronto.
Cajori, F. (1929). A History of Mathematical Notations, volume II: Notations Mainly in Higher Mathematics. Open Court Publishing Company, Chicago.
Carnap, R. (1929). Abriss der Logistik, mit besonderer Berücksichtigung der Relationentheorie und ihrer Anwendungen, volume 2 of Schriften zur wissenschaftlichen Weltauffassung. Springer Verlag, Vienna.
Carter, J. (2010). Diagrams and proofs in analysis. International Studies in the Philosophy of Science, 24(1):1–24.
Carter, J. (2021). “Free rides” in mathematics. Synthese, 199:10475–10498.
Carter, J. (2024). Introducing the Philosophy of Mathematical Practice. Cambridge University Press, Cambridge, UK.
Cauchy, A. (1846). Mémoire sur les fonctions de variables imaginaires. Comptes rendus des Séances de l’Académie des Sciences. Paris, 23:271–275. Reprinted in Oeuvres Completes, series 2, vol. 23, pp. 405–435, Gauthier-Villars, 1932.
Chase, W. G. and Simon, H. A. (1973). Perception in chess. Cognitive Psychology, 4:55–81.
Cheng, P. C.-H. (2020). Truth diagrams versus extant notations for propositional logic. Journal of Logic, Language and Information, 29(2): 121–161.
Chrisomalis, S. (2010). Numerical Notation: A Comparative History. Cambridge University Press, Cambridge, UK.
Chrisomalis, S. (2020). Reckonings: Numerals, Cognition, and History. Massachusetts Institute of Technology Press, Cambridge, MA.
Couturat, L., Ladd-Franklin, C., and Peirce, C. S. (1902). Symbolic logic. In Baldwin, J. M., editor, Dictionary of Philosophy and Psychology, pages 640–651. The Macmillan Company, London.
De Cruz, H. and De Smedt, J. (2010). Mathematical symbols as epistemic actions. Synthese, 190(1):1–17.
De Morgan, A. (1847). Formal Logic, or The calculus of inference, necessary and probable. Taylor and Walton, London.
De Toffoli, S. (2023). What are mathematical diagrams? Synthese, 200(86):1–29.
De Toffoli, S. and Giardino, V. (2014). An inquiry into the practice of proving in low-dimensional topology. Boston Studies in the History and the Philosophy of Science, 308:315–336.
Dedekind, R. (1888). Was sind und was sollen die Zahlen? Vieweg, Braunschweig. English translation by Wooster W. Beman, revised by William Ewald, in Ewald (1996), pp. 787–833.
Dehaene, S. (1992). Varieties of numerical abilities. Cognition, 44:1–42.
Durham, J. W. (1992). The introduction of “Arabic” numerals in European accounting. The Accounting Historians Journal, 19(2):25–55.
Dutilh Novaes, C. (2012). Formal Languages in Logic: A Philosophical and Cognitive Analysis. Cambridge University Press, Cambridge, UK.
Dutz, J. and Schlimm, D. (2021). Babbage’s guidelines for the design of mathematical notations. Studies in History and Philosophy of Science, 88:92–101.
Elkind, L. D. C. and Zach, R. (2023). The genealogy of ‘ .’ Review of Symbolic Logic, 16(3):862–899.
.’ Review of Symbolic Logic, 16(3):862–899. Enderton, H. B. (2001). A Mathematical Introduction to Logic. Harcourt Academic Press, San Diego, 2nd edition.
Ewald, W. (1996). From Kant to Hilbert: A Source Book in Mathematics. Clarendon Press, Oxford. Two volumes.
Foster, J. E. (1947). A number system without a zero-symbol. Mathematics Magazine, 21(1):39–41.
Frege, G. (1879). Begriffsschrift. Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Verlag Louis Nebert, Halle a/S. English translation: Begriffsschrift, A Formula Language, Modeled upon That for Arithmetic, in van Heijenoort (1967), pp. 1–82.
Frege, G. (1884). Die Grundlagen der Arithmetik. Verlag von Wilhelm Koebner, Breslau. English translation by J. L. Austin: The Foundations of Arithmetic, Basil Blackwell, Oxford, 1953.
Frege, G. (1984). Logical investigations. In Collected Papers on Mathematics, Logic, and Philosophy, pages 351–406. Basil Blackwell, Oxford. Edited by McGuinness, Brian.
Gentzen, G. (1935). Untersuchungen über das logische Schließen. Mathematische Zeitschrift, 39:176–210, 405–431. English translation: Investigations into logical deduction, in Szabo (1969), pages 68–131.
Girard, J.-Y. (1987). Linear logic. Theoretical Computer Science, 50:1–102.
Goldfarb, W., editor (1971). Jacques Herbrand: Logical Writings. D. Reidel Publishing Company, Dordrecht.
Goodman, N. (1968). Languages of Art: An Approach to a Theory of Symbols. Bobbs-Merrill, Indianapolis.
Greenberg, J. H. (1978). Generalizations about numeral systems. In Greenberg, J. H., Ferguson, C. A., and Moravcsik, E. A., editors, Universals of Human Language, volume 3: Word Structure, pages 249–295. Stanford University Press, Stanford, CA.
Grosholz, E. R. (2007). Representation and Productive Ambiguity in Mathematics and the Sciences. Oxford University Press, Oxford.
Haffner, E. (2021). The shaping of Dedekind’s rigorous mathematics: What do Dedekind’s drafts tell us about his ideal of rigor? Notre Dame Journal of Formal Logic, 62(1):5–31.
Haigh, T. and Ceruzzi, P. E. (2021). A New History of Modern Computing. Massachusetts Institute of Technology Press, Cambridge, MA.
Heath, T. L. (1910). Diophantus of Alexandria: A Study in the History of Greek Algebra. Cambridge University Press, New York, 2nd edition.
Heyting, A. (1930). Die formalen Regeln der intuitionistischen Logik. Sitzungsberichte der Preussischen Akademie der Wissenschaften, pages 42–56.
Hutchins, E. (1995). Cognition in the Wild. Massachusetts Institute of Technology Press, Cambridge, MA.
Jevons, W. S. (1896). Studies in Deductive Logic: A Manual for Students. Macmillan, New York, 3rd edition.
Kauffman, L. H. (2001). Knots and Physics. World Scientific, Singapore.
Kirsh, D. (1990). When is information explicitly represented? The Vancouver Studies in Cognitive Science, pages 340–365.
Kirsh, D. (2003). Implicit and explicit representation. In Nadel, L., editor, Encyclopedia of Cognitive Science, pages 478–481. Nature Publishing, London.
Kirsh, D. (2010). Thinking with external representations. AI & Society, 25:441–454.
Klein, U. (2001). Paper tools in experimental cultures. Studies in the History and Philosophy of Science, 32(2):265–302.
Klein, U. (2002). Experiments, Models, Paper Tools: Cultures of Organic Chemistry in the Nineteenth Century. Stanford University Press, Stanford, CA.
Knobloch, E., editor (2016). Gottfried Wilhelm Leibniz. De quadratura arithmetica circuli ellipseos et hyperbolae cujus corollarium est trigonometria sine tabulis. Springer Spektrum, Berlin.
Krämer, S. (2003). Writing, notational iconicity, calculus: On writing as a cultural technique. Modern Language Notes: German Issue, 118(3):518–537.
Kripke, S. (2023). Wittgenstein, Russell, and our concept of the natural numbers. In Posy, C. and Ben-Menahem, Y., editors, Mathematical Knowledge, Objects, and Applications: Essays in Memory of Mark Steiner, pages 137–156. Springer, Cham.
Lakatos, I. (1976). Proofs and Refutations. Cambridge University Press, Cambridge, UK. Edited by Worrall, John and Zahar, Elie.
Landy, D., Allen, C., and Zednik, C. (2014). A perceptual account of symbolic reasoning. Frontiers in Psychology, 5(275):1–10.
Larkin, J. H. and Simon, H. A. (1987). Why a diagram is (sometimes) worth ten thousand words. Cognitive Science, 11:65–99.
Lengnink, K. and Schlimm, D. (2010). Learning and understanding numeral systems: Semantic aspects of number representations from an educational perspective. In Löwe, B. and Müller, T., editors, Philosophy of Mathematics: Sociological Aspects and Mathematical Practice, pages 235–264. College Publications, London.
Lorayne, H. (1992). Miracle Math: How to Develop a Calculator in Your Head. Barnes & Noble, New York.
Manders, K. (1996). Diagram contents and representational granularity. In Seligmann, J. and Westerstahl, D., editors, Logic Language and Computation, pages 389–404. Stanford University Press, Stanford, CA.
Manders, K. (2008). The Euclidean diagram (1995). In Mancosu, P., editor, The Philosophy of Mathematical Practice, pages 80–133. Oxford University Press, Oxford.
Menary, R. and Gillett, A. (2022). The tools of enculturation. Topics in Cognitive Science, 14:363–387.
Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2):81–97.
Miller, K. F., Kelly, M., and Zhou, X. (2005). Learning mathematics in China and the United States: Cross-cultural insights into the nature and course of preschool mathematical development. In Campbell, J. I. D., editor, Handbook of Mathematical Cognition, pages 163–178. Psychology Press, Hove, UK.
Nicod, J. (1917). A reduction in the number of the primitive propositions of logic. Proceedings of the Cambridge Philosophical Society, 19:32–41.
Norman, D. (2013). The Design of Everyday Things. Massachusetts Institute of Technology Press, Cambridge, MA, revised and expanded edition.
Nuerk, H.-C., Moeller, K., and Willmes, K. (2015). Multi-digit number processing. overview, conceptual clarifications, and language influences. In Cohen Kadosh, R. and Dowker, A., editors, The Oxford Handbook of Numerical Cognition, chapter 7, pages 106–139. Oxford University Press, Oxford.
Nuerk, H.-C., Wegner, U., and Willmes, K. (2001). Decade breaks in the mental number line? putting the tens and units back in different bins. Cognition, 82(1):B25–B33.
Palmer, S. E. (1978). Fundamental aspects of cognitive representation. In Rosch, E. and Lloyd, B., editors, Cognition and Categorization, pages 259–303. Lawrence Elbaum Associates, Hillsdale, NJ.
Pantsar, M. (2021). Cognitive and computational complexity: Considerations from mathematical problem solving. Erkenntnis, 86:961–997.
Pantsar, M. (2024). Numerical Cognition and the Epistemology of Arithmetic. Cambridge University Press, Cambridge, UK.
Paoli, F. (2002). Substructural Logics: A Primer. Springer, Dordrecht.
Peirce, C. S. (1870). On an improvement in Boole’s calculus of logic. Proceedings of the American Academy of Arts and Sciences, 7:250–261. Reprinted in Peirce (1966), III, pp. 27–98.
Peirce, C. S. (1885). On the algebra of logic: A contribution to the philosophy of notation. American Journal of Mathematics, 7(2):180–196. Reprinted in Peirce (1966), III, pp. 210–249.
Peirce, C. S. (1897). The logic of relatives. The Monist, 7(2):161–217.
Peirce, C. S. (1960–1966). Collected Papers. Harvard University Press, Cambridge, MA. Four volumes. Reprint of 1931–1958, eight volumes. Edited by Charles Hartshorne and Paul Weiss.
Polya, G. (1954). Mathematics and Plausible Reasoning, volume 1: Induction and Analogy in Mathematics. Princeton University Press, Princeton, NJ.
Ramachandran, V. S. and Hubbard, E. M. (2001). Synaesthesia: A window into perception, thought and language. Journal of Consciousness Studies, 8(12):3–34.
Ramsey, F. P. (1927). Facts and propositions. Proceedings of the Aristotelian Society, Supplementary Volumes, vol. 7, Mind, Objectivity and Fact (1927), pp. 153–170.
Saidan, A. S., editor (1978). The Arithmetic of Al-Uqlʙ;disʙ;. D. Reidel Publishing Company, Dordrecht.
Saxe, G. B. (1981). Body parts as numerals: A developmental analysis of numeration among the Oksapmin in Papua New Guinea. Child Development, 52(1):306–316.
Schlimm, D. (2013). Axioms in mathematical practice. Philosophia Mathematica (Series III), 21(1):37–92.
Schlimm, D. (2018). Numbers through numerals: The constitutive role of external representations. In Bangu, S., editor, Naturalizing Logico-Mathematical Knowledge: Approaches from Philosophy, Psychology and Cognitive Science. Routledge, Abingdon-on-Thames, UK.
Schlimm, D. (2021). Peano on symbolization, design principles for notations, and the dot notation. Philosophia Scientiæ, 25(1):139–170.
Schlimm, D. (2022). Tables as powerful representational tools. In Giardino, V., Linker, S., Burns, R., Bellucci, F., Boucheix, J.-M., and Viana, P., editors, Diagrammatic Representation and Inference. 13th International Conference, Diagrams 2022, Rome, Italy, September 14–16, 2022, Proceedings, pages 185–201, Springer, New York.
Schlimm, D. and Neth, H. (2008). Modeling ancient and modern arithmetic practices: Addition and multiplication with Arabic and Roman numerals. In Sloutsky, V., Love, B., and McRae, K., editors, Proceedings of the 30th Annual Meeting of the Cognitive Science Society, pages 2097–2102, Austin, TX. Cognitive Science Society.
Schlimm, D. and Skosnik, K. (2011). Symbols for nothing: Different symbolic roles of zero and their gradual emergence in Mesopotamia. In Cupillari, A., editor, Proceedings of the 2010 Meeting of the Canadian Society for History and Philosophy of Mathematics, May 29–31, Montreal, volume 23, pages 257–266.
Schlimm, D. and Waszek, D. (2020). Multiple readability in principle and practice: Existential graphs and complex symbols. Logique & Analyse, 251:231–260.
Sheffer, H. M. (1913). A set of five postulates for Boolean algebras, with application to logical constants. Transactions of the American Mathematical Society, 14(4):481–488.
Shimojima, A. (2015). Semantic Properties of Diagrams and Their Cognitive Potentials. CSLI Publications, Stanford, CA.
Siegmund-Schultze, R. (1991). Mathematics and ideology in fascist Germany. In Woodward, W. R. and Cohen, R. S., editors, World Views and Scientific Discipline Formation, pages 89–95. Kluwer Academic Publishers, Berlin.
Sigler, L. (2002). Fibonacci’s Liber Abaci. A Translation into Modern English of Leonardo Pisano’s Book of Calculation. Springer, New York.
Stamm, E. (1911). Beitrag zur Algebra der Logik. Monatshefte für Mathematik und Physik, 22(1):137–149.
Stenning, K. (2000). Distinctions with differences: Comparing criteria for distinguishing diagrammatic from sentential systems. In Anderson, M., Cheng, P., and Haarslev, V., editors, Theory and Application of Diagrams, volume 1889 of Lecture Notes in Artificial Intelligence, pages 132–148, Springer, Berlin.
Stenning, K. (2002). Seeing Reason: Image and Language in Learning to Think. Oxford University Press, Oxford.
Stjernfelt, F. (2007). Diagrammatology: An Investigation of the Borderlines of Phenomenology, Ontology, and Semiotics. Springer, Dordrecht.
Strickland, L. and Lewis, H. R., editors (2022). Leibniz on Binary: The Invention of Computer Arithmetic. Massachusetts Institute of Technology Press, Cambridge, MA.
Szabo, M. E., editor (1969). The Collected Papers of Gerhard Gentzen, North-Holland, Amsterdam.
Tolchinsky, L. (2003). The Cradle of Culture and What Children Know About Writing and Numbers Before Being Taught. Erlbaum Associates, Mahwah, NJ.
Troelstra, A. S. (1992). Lectures on Linear Logic. CSLI Publications, Stanford.
Tufte, E. R. (2001). The Visual Display of Quantitative Information. Graphics Press, Cheshire, CT, 2nd edition.
van Heijenoort, J. (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931. Harvard University Press, Cambridge, MA.
Venn, J. (1880). Review of Frege’s Begriffsschrift. Mind, 5(18):297.
Vold, K. and Schlimm, D. (2020). Extended mathematical cognition: External representations with non-derived content. Synthese, 179(9):3757–3777.
Wagner, R. (2017). Making and Breaking Mathematical Sense: Histories and Philosophies of Mathematical Practice. Princeton University Press, Princeton.
Warde, B. (1955). The crystal goblet, or Printing should be invisible. In Jacob, H., editor, The Crystal Goblet. Sixteen Essays on Typography, pages 11–17. The Sylvan Press, London.
Waszek, D. (2024). Informational equivalence but computational differences? Herbert Simon on representations in scientific practice. Minds and Machines, 34:93–116.
Wege, T., Batchelor, S., Inglis, M., Mistry, H., and Schlimm, D. (2020). Iconicity in mathematical notation: Commutativity and symmetry. Journal of Numerical Cognition, 6(3):378–392.
Whitehead, A. N. and Russell, B. (1910). Principia Mathematica, volume 1. Cambridge University Press, Cambridge.
Widom, T. R. and Schlimm, D. (2012). Methodological reflections on typologies for numeral systems. Science in Context, 25(2):155–195.
Wittgenstein, L. (1922). Tractatus Logico-Philosophicus. Kegan Paul, Trench, Trubner & Co., London.
Zhang, J. and Norman, D. A. (1995). A representational analysis of numeration systems. Cognition, 57:271–295.

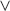 .’ Review of Symbolic Logic, 16(3):862–899.
.’ Review of Symbolic Logic, 16(3):862–899. Loading metrics...
Loading metrics...


