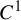Refine listing
Actions for selected content:
240 results in 11Jxx
The structure of Lonely Runner spectra
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 24 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUANTITATIVE GROWTH OF LINEAR RECURRENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-34
-
- Article
- Export citation
Linearly exponential checking is enough for the lonely runner conjecture and some of its variants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 October 2025, e164
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HODGE CYCLES AND QUADRATIC RELATIONS BETWEEN HOLOMORPHIC PERIODS ON CM ABELIAN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new class of α-Farey maps and an application to normal numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
METRICAL PROPERTIES OF CONTINUED FRACTION AND LÜROTH SERIES EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
Diophantine approximations with restrained denominators. Balance condition on decay and growth rates
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-36
-
- Article
- Export citation
On congruence subgroups generated by two parabolic rational matrices
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-20
-
- Article
- Export citation
Ergodicity and algebraicity of the fast and slow triangle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-35
-
- Article
- Export citation
Number of solutions to a special type of unit equations in two unknowns, III
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 07 August 2025, pp. 737-784
- Print publication:
- November 2025
-
- Article
- Export citation
Functional Transcendence of Periods and the Geometric André–Grothendieck Period Conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On inhomogeneous Poissonian pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 17-27
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FONCTIONS ADDITIVES EN BASE DE CANTOR LE LONG DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 06 May 2025, pp. 1807-1865
- Print publication:
- September 2025
-
- Article
- Export citation
NOMBRE DE PETITS POINTS SUR UNE VARIÉTÉ ABÉLIENNE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 705-761
- Print publication:
- May 2025
-
- Article
- Export citation
MAILLET’S PROPERTY AND MAHLER’S CONJECTURE ON LIOUVILLE NUMBERS FAIL FOR MATRICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 106-127
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IRRATIONALITY OF ZEROS OF POLYGAMMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-11
-
- Article
- Export citation
Dynamical Diophantine approximation and shrinking targets for
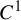 $C^{1}$ weakly conformal IFSs with overlaps
$C^{1}$ weakly conformal IFSs with overlaps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1777-1826
- Print publication:
- June 2025
-
- Article
- Export citation
ON PERFECT POWERS AS SUMS OR DIFFERENCES OF TWO k-GENERALISED PELL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 227-236
- Print publication:
- October 2025
-
- Article
- Export citation
Effective approximation to complex algebraic numbers by quadratic numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 262-269
- Print publication:
- March 2025
-
- Article
- Export citation
Uniformity of quasi-integral points of bounded degree in higher-dimensional orbits
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 15-29
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation