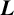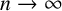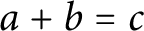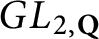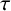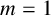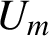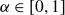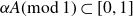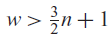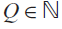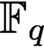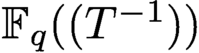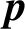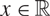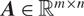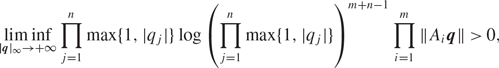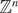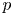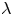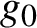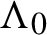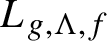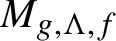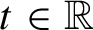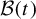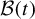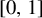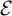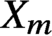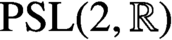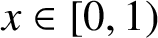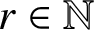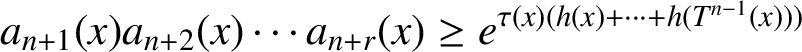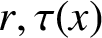Refine listing
Actions for selected content:
237 results in 11Jxx
APÉRY LIMITS FOR ELLIPTIC
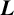 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on spaces of almost periodic functions with values in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 953-962
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetic derivatives through geometry of numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 906-923
- Print publication:
- December 2022
-
- Article
- Export citation
Special curves in modular surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 1-18
- Print publication:
- March 2023
-
- Article
- Export citation
NOTES ON THE DPRM PROPERTY FOR LISTABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 November 2021, pp. 273-312
- Print publication:
- March 2022
-
- Article
- Export citation
A DIMENSIONAL RESULT ON THE PRODUCT OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 357-385
- Print publication:
- December 2022
-
- Article
- Export citation
ON TRANSCENDENTAL CONTINUED FRACTIONS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 392-403
- Print publication:
- June 2022
-
- Article
- Export citation
Remarks about inhomogeneous pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 369-386
- Print publication:
- September 2022
-
- Article
- Export citation
QUANTITATIVE ESTIMATE FOR THE MEASURE OF A SET OF REAL NUMBERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 411-433
- Print publication:
- May 2022
-
- Article
- Export citation
MAHLER’S AND KOKSMA’S CLASSIFICATIONS IN FIELDS OF POWER SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 07 June 2021, pp. 355-371
- Print publication:
- June 2022
-
- Article
- Export citation
ELLIPTIC CURVES AND
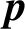 $\boldsymbol {p}$-ADIC ELLIPTIC TRANSCENDENCE
$\boldsymbol {p}$-ADIC ELLIPTIC TRANSCENDENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 21 May 2021, pp. 31-36
- Print publication:
- February 2022
-
- Article
- Export citation
Multiplicatively badly approximable matrices up to logarithmic factors
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 685-703
- Print publication:
- May 2022
-
- Article
- Export citation
On simultaneous rational approximation to a p-adic number and its integral powers, II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 07 May 2021, pp. 317-337
-
- Article
- Export citation
Continuity of Hausdorff dimension across generic dynamical Lagrange and Markov spectra II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 1898-1907
- Print publication:
- June 2022
-
- Article
- Export citation
On the distribution of nonprimitive lattice points in the plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 198-207
- Print publication:
- March 2022
-
- Article
- Export citation
The bifurcation locus for numbers of bounded type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2239-2269
- Print publication:
- July 2022
-
- Article
- Export citation
Nonspecial varieties and generalised Lang–Vojta conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 10 February 2021, e11
-
- Article
-
- You have access
- Open access
- Export citation
ON GOOD APPROXIMATIONS AND THE BOWEN–SERIES EXPANSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 25 January 2021, pp. 45-58
- Print publication:
- August 2021
-
- Article
- Export citation
HAUSDORFF DIMENSION FOR THE SET OF POINTS CONNECTED WITH THE GENERALIZED JARNÍK–BESICOVITCH SET
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2020, pp. 1-29
- Print publication:
- February 2022
-
- Article
- Export citation
On the prime factors of the iterates of the Ramanujan τ–function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 11 November 2020, pp. 1031-1047
-
- Article
- Export citation