Let 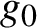$g_0$ be a smooth pinched negatively curved Riemannian metric on a complete surface N, and let 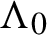$\Lambda _0$ be a basic hyperbolic set of the geodesic flow of 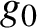$g_0$ with Hausdorff dimension strictly smaller than two. Given a small smooth perturbation g of 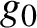$g_0$ and a smooth real-valued function f on the unit tangent bundle to N with respect to g, let 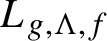$L_{g,\Lambda ,f}$ (respectively 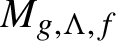$M_{g,\Lambda ,f}$) be the Lagrange (respectively Markov) spectrum of asymptotic highest (respectively highest) values of f along the geodesics in the hyperbolic continuation 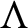$\Lambda $ of 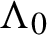$\Lambda _0$. We prove that for generic choices of g and f, the Hausdorff dimensions of the sets 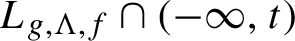$L_{g,\Lambda , f}\cap (-\infty , t)$ vary continuously with 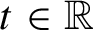$t\in \mathbb {R}$ and, moreover, 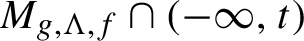$M_{g,\Lambda , f}\cap (-\infty , t)$ has the same Hausdorff dimension as 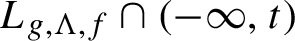$L_{g,\Lambda , f}\cap (-\infty , t)$ for all 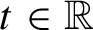$t\in \mathbb {R}$.