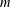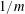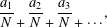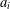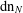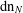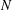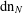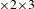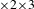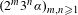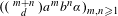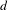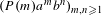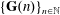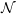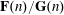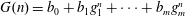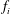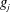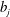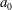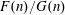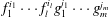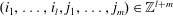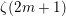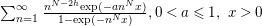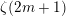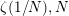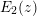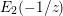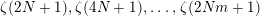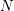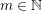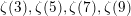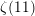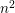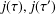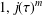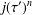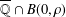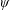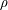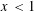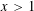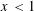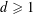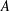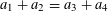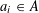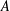Refine listing
Actions for selected content:
237 results in 11Jxx
LONELY RUNNERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 677-701
- Print publication:
- 2019
-
- Article
- Export citation
GENERALIZED CONTINUED FRACTION EXPANSIONS WITH CONSTANT PARTIAL DENOMINATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 272-288
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A polynomial-exponential variation of Furstenberg’s
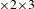 $\times 2\times 3$ theorem
$\times 2\times 3$ theorem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1729-1737
- Print publication:
- July 2020
-
- Article
- Export citation
Numbers with Almost all Convergents in a Cantor Set
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 869-875
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Metrical Results on the Distribution of Fractional Parts of Powers of Real Numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 505-521
-
- Article
- Export citation
The Quotient Problem for Entire Functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 26 October 2018, pp. 479-489
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
GENERALIZED LAMBERT SERIES, RAABE’S COSINE TRANSFORM AND A GENERALIZATION OF RAMANUJAN’S FORMULA FOR
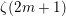 $\unicode[STIX]{x1D701}(2m+1)$
$\unicode[STIX]{x1D701}(2m+1)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 04 October 2018, pp. 232-293
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
LINEAR INDEPENDENCE OF POWERS OF SINGULAR MODULI OF DEGREE THREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 September 2018, pp. 42-50
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ON MAHLER’S CLASSIFICATION OF
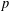 $p$-ADIC NUMBERS
$p$-ADIC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 30 July 2018, pp. 203-211
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
SOME HYPERGEOMETRIC INTEGRALS FOR LINEAR FORMS IN ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 372-375
- Print publication:
- December 2018
-
- Article
-
- You have access
- Open access
- Export citation
On linear independence measures of the values of Mahler functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 1297-1311
- Print publication:
- December 2018
-
- Article
- Export citation
SHIDLOVSKY’S MULTIPLICITY ESTIMATE AND IRRATIONALITY OF ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 145-172
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON A COMPLETE SOLUTION OF A PROBLEM POSED BY K. MAHLER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 60-63
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
A mass transference principle for systems of linear forms and its applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1014-1047
- Print publication:
- May 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pair correlation for quadratic polynomials mod 1
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 960-983
- Print publication:
- May 2018
-
- Article
- Export citation
HAUSDORFF DIMENSION OF THE SET APPROXIMATED BY IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 267-283
- Print publication:
- 2018
-
- Article
- Export citation
HAUSDORFF MEASURE OF SETS OF DIRICHLET NON-IMPROVABLE NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 19 April 2018, pp. 502-518
- Print publication:
- 2018
-
- Article
- Export citation
TRANSCENDENTAL SUMS RELATED TO THE ZEROS OF ZETA FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 875-897
- Print publication:
- 2018
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 19 June 2018, pp. 679-700
- Print publication:
- 2018
-
- Article
- Export citation