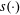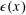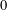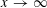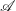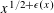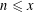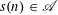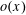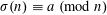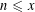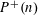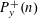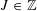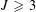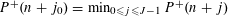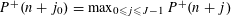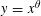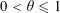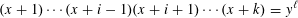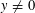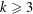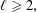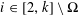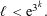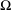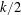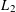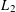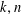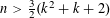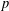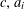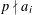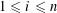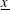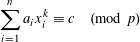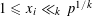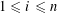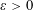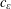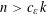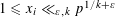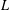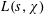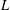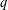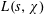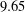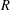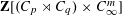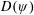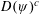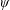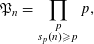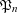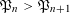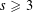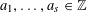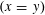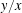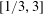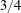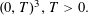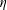Contents
Research Article
ALGEBRAIC TORI AS DEGENERATIONS OF ABELIAN VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2018, pp. 303-329
-
- Article
-
- You have access
- HTML
- Export citation
DIVISOR-SUM FIBERS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 330-342
-
- Article
- Export citation
SUR LES PLUS GRANDS FACTEURS PREMIERSD’ENTIERS CONSÉCUTIFS
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2018, pp. 343-379
-
- Article
- Export citation
VARIANTS OF ERDŐS–SELFRIDGE SUPERELLIPTIC CURVES AND THEIR RATIONAL POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 380-386
-
- Article
- Export citation
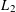 $L_{2}$ -SMALL DEVIATIONS FOR WEIGHTED STATIONARY PROCESSES
$L_{2}$ -SMALL DEVIATIONS FOR WEIGHTED STATIONARY PROCESSES
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 387-405
-
- Article
- Export citation
REDUCTION OF DIMENSION AS A CONSEQUENCE OF NORM-RESOLVENT CONVERGENCE AND APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 406-429
-
- Article
- Export citation
SOLUTIONS TO DIAGONAL CONGRUENCES WITH VARIABLES RESTRICTED TO A BOX
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 430-444
-
- Article
- Export citation
EXPLICIT ZERO-FREE REGIONS FOR DIRICHLET
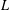 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2018, pp. 445-474
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
-
- Article
- Export citation
Corrigendum
STABLY FREE MODULES OVER
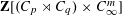 $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{m}]$ ARE FREE
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{m}]$ ARE FREE
-
- Published online by Cambridge University Press:
- 17 April 2018, pp. 497-501
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
HAUSDORFF MEASURE OF SETS OF DIRICHLET NON-IMPROVABLE NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2018, pp. 502-518
-
- Article
- Export citation
DENOMINATORS OF BERNOULLI POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2018, pp. 519-541
-
- Article
- Export citation
THE DENSITY OF NUMBERS REPRESENTED BY DIAGONAL FORMS OF LARGE DEGREE
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. 542-550
-
- Article
- Export citation
TRIANGLES CAPTURING MANY LATTICE POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2018, pp. 551-582
-
- Article
- Export citation
ASYMPTOTIC BEHAVIOUR OF THE SPECTRA OF SYSTEMS OF MAXWELL EQUATIONS IN PERIODIC COMPOSITE MEDIA WITH HIGH CONTRAST
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. 583-605
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 64 Issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 May 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
MTK volume 64 Issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 May 2018, pp. b1-b2
-
- Article
-
- You have access
- Export citation