Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-06T13:26:21.745Z Has data issue: false hasContentIssue false
  • English
  • Français

HAUSDORFF MEASURE OF SETS OF DIRICHLET NON-IMPROVABLE NUMBERS

Part of: Diophantine approximation, transcendental number theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  19 April 2018

Mumtaz Hussain ,
Dmitry Kleinbock ,
Nick Wadleigh  and
Bao-Wei Wang
Mumtaz Hussain
Affiliation:
Department of Mathematics and Statistics, La Trobe University, PO Box 199, Bendigo 3552, Australia email m.hussain@latrobe.edu.au
Dmitry Kleinbock
Affiliation:
Brandeis University, Waltham, MA 02454-9110, U.S.A. email kleinboc@brandeis.edu
Nick Wadleigh
Affiliation:
Brandeis University, Waltham, MA 02454-9110, U.S.A. email wadleigh@brandeis.edu
Bao-Wei Wang
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, 430074 Wuhan, China email bwei_wang@hust.edu.cn
Get access

Abstract

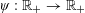Let $\unicode[STIX]{x1D713}:\mathbb{R}_{+}\rightarrow \mathbb{R}_{+}$ be a non-increasing function. A real number $x$ is said to be 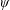$\unicode[STIX]{x1D713}$-Dirichlet improvable if it admits an improvement to Dirichlet’s theorem in the following sense: the system

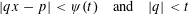$$\begin{eqnarray}|qx-p|<\unicode[STIX]{x1D713}(t)\quad \text{and}\quad |q|<t\end{eqnarray}$$
has a non-trivial integer solution for all large enough $t$. Denote the collection of such points by 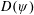$D(\unicode[STIX]{x1D713})$. In this paper we prove that the Hausdorff measure of the complement 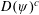$D(\unicode[STIX]{x1D713})^{c}$ (the set of 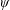$\unicode[STIX]{x1D713}$-Dirichlet non-improvable numbers) obeys a zero-infinity law for a large class of dimension functions. Together with the Lebesgue measure-theoretic results established by Kleinbock and Wadleigh [A zero-one law for improvements to Dirichlet’s theorem. Proc. Amer. Math. Soc.146 (2018), 1833–1844], our results contribute to building a complete metric theory for the set of Dirichlet non-improvable numbers.

MSC classification

Primary: 11J83: Metric theory 11K60: Diophantine approximation
Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 502 - 518
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beresnevich, V., Dickinson, D. and Velani, S., Measure theoretic laws for lim sup sets. Mem. Amer. Math. Soc. 179(846) 2006.Google Scholar
Beresnevich, V. and Velani, S., A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) 2006, 971–992.CrossRefGoogle Scholar
Bernik, V. I. and Dodson, M. M., Metric Diophantine Approximation on Manifolds (Cambridge Tracts in Mathematics 137 ), Cambridge University Press (Cambridge, 1999).CrossRefGoogle Scholar
Davenport, H. and Schmidt, W. M., Dirichlet’s theorem on diophantine approximation. In Symposia Mathematica (INDAM, Rome, 1968/69), Vol. IV, Academic (London, 1970), 113–132.Google Scholar
Falconer, K., Fractal Geometry, 3rd edn., Wiley (Chichester, 2014).Google Scholar
Iosifescu, M. and Kraaikamp, C., Metrical Theory of Continued Fractions, Kluwer (Dordrecht, 2002).CrossRefGoogle Scholar
Jarník, V., Über die simultanen diophantischen approximationen. Math. Z. 33 1931, 505–543.CrossRefGoogle Scholar
Khintchine, A. Y., Continued Fractions, Noordhoff (Groningen, 1963); translated by Peter Wynn.Google Scholar
Khinchin, A. Y., Continued Fractions, The University of Chicago Press (Chicago, IL–London, 1964).Google Scholar
Kleinbock, D. and Wadleigh, N., A zero-one law for improvements to Dirichlet’s theorem. Proc. Amer. Math. Soc. 146 2018, 1833–1844.CrossRefGoogle Scholar
Wang, B.-W. and Wu, J., Hausdorff dimension of certain sets arising in continued fraction expansions. Adv. Math. 218(5) 2008, 1319–1339.CrossRefGoogle Scholar