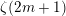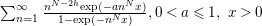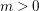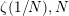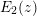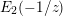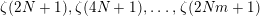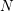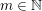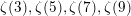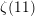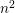1 Introduction
In his address to the American Mathematical Society on September 5, 1941 [Reference Rademacher54], Hans Rademacher writes “…the impression may have prevailed that analytic number theory deals foremost with asymptotic expressions for arithmetical functions. This view, however, overlooks another side of analytic number theory, which I may indicate by the words “identities”, “group-theoretical arguments”, “structural considerations”. This line of research is not yet so widely known; it may very well be that methods of its type will lead to the “deeper” results, will reveal the sources of some of the results of the first direction of approach.”
Indeed, the developments that have taken place, since Rademacher’s time, in the theory of partitions, theory of modular forms, mock modular forms and harmonic Maass forms [Reference Bringmann, Folsom, Ono and Rolen15], to name a few, prove that his assessment of the impact of this other side of analytic number theory was correct. In the present paper, we offer the reader new examples further corroborating Rademacher’s claim, namely, we derive important results which, on one hand, hint connections with the modular world and on the other hand, have applications toward irrationality/transcendence of certain values.
In [Reference Dixit and Maji21, Theorem 1.1], a transformation of the series ![]() $\sum _{n=1}^{\infty }\frac{n^{N-2h}}{e^{n^{N}x}-1}$ was obtained for any positive integer
$\sum _{n=1}^{\infty }\frac{n^{N-2h}}{e^{n^{N}x}-1}$ was obtained for any positive integer ![]() $N$ and any integer
$N$ and any integer ![]() $h$. Ramanujan, by the way, explicitly wrote down this exact same series on page
$h$. Ramanujan, by the way, explicitly wrote down this exact same series on page ![]() $332$ of his Lost Notebook [Reference Ramanujan56] but he did not give any transformation for it. Kanemitsu et al. [Reference Kanemitsu, Tanigawa and Yoshimoto35] were the first to obtain a transformation of this series, however, they considered the case
$332$ of his Lost Notebook [Reference Ramanujan56] but he did not give any transformation for it. Kanemitsu et al. [Reference Kanemitsu, Tanigawa and Yoshimoto35] were the first to obtain a transformation of this series, however, they considered the case ![]() $0<h\leqslant N/2$ only. In fact, in [Reference Dixit and Maji21, Theorem 1.1], it was observed that working out the transformation in the remaining two cases, that is
$0<h\leqslant N/2$ only. In fact, in [Reference Dixit and Maji21, Theorem 1.1], it was observed that working out the transformation in the remaining two cases, that is ![]() $h>N/2$ and
$h>N/2$ and ![]() $h\leqslant 0$, in the case when
$h\leqslant 0$, in the case when ![]() $N$ is an odd positive integer, enables us to decode valuable information in that when
$N$ is an odd positive integer, enables us to decode valuable information in that when ![]() $N=1$, together these cases give, as a special case, Ramanujan’s following famous formula for
$N=1$, together these cases give, as a special case, Ramanujan’s following famous formula for ![]() $\unicode[STIX]{x1D701}(2m+1),m\neq 0$ [Reference Ramanujan55, page 173, Ch. 14, Entry 21(i)], [Reference Ramanujan56, pages 319–320, formula (28)], [Reference Berndt8, pages 275–276]:
$\unicode[STIX]{x1D701}(2m+1),m\neq 0$ [Reference Ramanujan55, page 173, Ch. 14, Entry 21(i)], [Reference Ramanujan56, pages 319–320, formula (28)], [Reference Berndt8, pages 275–276]:
For ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ with
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ with ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$ and
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$ and ![]() $m\in \mathbb{Z},m\neq 0$,
$m\in \mathbb{Z},m\neq 0$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-m}\bigg\{\frac{1}{2}\unicode[STIX]{x1D701}(2m+1)+\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}}{e^{2\unicode[STIX]{x1D6FC}n}-1}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD})^{-m}\bigg\{\frac{1}{2}\unicode[STIX]{x1D701}(2m+1)+\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}}{e^{2\unicode[STIX]{x1D6FD}n}-1}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2^{2m}\mathop{\sum }_{j=0}^{m+1}\frac{(-1)^{j}B_{2j}B_{2m+2-2j}}{(2j)!(2m+2-2j)!}\unicode[STIX]{x1D6FC}^{m+1-j}\unicode[STIX]{x1D6FD}^{j},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-m}\bigg\{\frac{1}{2}\unicode[STIX]{x1D701}(2m+1)+\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}}{e^{2\unicode[STIX]{x1D6FC}n}-1}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD})^{-m}\bigg\{\frac{1}{2}\unicode[STIX]{x1D701}(2m+1)+\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}}{e^{2\unicode[STIX]{x1D6FD}n}-1}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2^{2m}\mathop{\sum }_{j=0}^{m+1}\frac{(-1)^{j}B_{2j}B_{2m+2-2j}}{(2j)!(2m+2-2j)!}\unicode[STIX]{x1D6FC}^{m+1-j}\unicode[STIX]{x1D6FD}^{j},\end{eqnarray}$$ where for ![]() $j\geqslant 0$,
$j\geqslant 0$, ![]() $B_{j}:=B_{j}(0)$ is the
$B_{j}:=B_{j}(0)$ is the ![]() $j$th Bernoulli number and
$j$th Bernoulli number and ![]() $B_{j}(a)$ is the
$B_{j}(a)$ is the ![]() $j$th Bernoulli polynomial defined by
$j$th Bernoulli polynomial defined by
The formula (1.1) was long forgotten before Grosswald [Reference Grosswald28] revived it and also obtained its generalizations [Reference Grosswald27], [Reference Grosswald29]. Some other formulas for ![]() $\unicode[STIX]{x1D701}(2m+1)$ were obtained by Terras [Reference Terras62], [Reference Terras63]. Ramanujan’s formula has a very rich history for which we refer the reader to a recent paper [Reference Berndt, Straub, Montgomery, Nikeghbali and Rassias13]. A contemporary interpretation of the above formula, as given for instance in [Reference Gun, Murty and Rath32], is that it encodes fundamental transformation properties of Eisenstein series on the full modular group and their Eichler integrals. This observation is extended in [Reference Berndt and Straub12, Section 5] to weight
$\unicode[STIX]{x1D701}(2m+1)$ were obtained by Terras [Reference Terras62], [Reference Terras63]. Ramanujan’s formula has a very rich history for which we refer the reader to a recent paper [Reference Berndt, Straub, Montgomery, Nikeghbali and Rassias13]. A contemporary interpretation of the above formula, as given for instance in [Reference Gun, Murty and Rath32], is that it encodes fundamental transformation properties of Eisenstein series on the full modular group and their Eichler integrals. This observation is extended in [Reference Berndt and Straub12, Section 5] to weight ![]() $2k+1$ Eisenstein series of level
$2k+1$ Eisenstein series of level ![]() $2$ through secant Dirichlet series. Ramanujan’s formula also has applications in theoretical computer science [Reference Kirschenhofer and Prodinger38] in the analysis of special data structures and algorithms. More specifically, it is used there to achieve certain distribution results on random variables related to dynamic data structures called “tries”.
$2$ through secant Dirichlet series. Ramanujan’s formula also has applications in theoretical computer science [Reference Kirschenhofer and Prodinger38] in the analysis of special data structures and algorithms. More specifically, it is used there to achieve certain distribution results on random variables related to dynamic data structures called “tries”.
The transformation for the series ![]() $\sum _{n=1}^{\infty }\frac{n^{N-2h}}{e^{n^{N}x}-1}$ for an odd integer
$\sum _{n=1}^{\infty }\frac{n^{N-2h}}{e^{n^{N}x}-1}$ for an odd integer ![]() $N\geqslant 1$ in the aforementioned two cases
$N\geqslant 1$ in the aforementioned two cases ![]() $h>N/2$ and
$h>N/2$ and ![]() $h\leqslant 0$ also gives an elegant generalization of Ramanujan’s formula [Reference Dixit and Maji21, Theorem 1.2] given below.
$h\leqslant 0$ also gives an elegant generalization of Ramanujan’s formula [Reference Dixit and Maji21, Theorem 1.2] given below.
Let ![]() $N$ be an odd positive integer and
$N$ be an odd positive integer and ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$. Then for
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$. Then for ![]() $m\in \mathbb{Z},m\neq 0$,
$m\in \mathbb{Z},m\neq 0$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-\frac{2Nm}{N+1}}\biggl(\frac{1}{2}\unicode[STIX]{x1D701}(2Nm+1)+\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm-1}}{\text{exp}((2n)^{N}\unicode[STIX]{x1D6FC})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD}^{\frac{2N}{N+1}})^{-m}\frac{2^{2m(N-1)}}{N}\biggl(\frac{1}{2}\unicode[STIX]{x1D701}(2m+1)+(-1)^{\frac{N+3}{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}}{\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{m+\frac{N+3}{2}}2^{2Nm}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}+m\rfloor }\frac{(-1)^{j}B_{2j}B_{N+1+2N(m-j)}}{(2j)!(N+1+2N(m-j))!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)}{N+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-\frac{2Nm}{N+1}}\biggl(\frac{1}{2}\unicode[STIX]{x1D701}(2Nm+1)+\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm-1}}{\text{exp}((2n)^{N}\unicode[STIX]{x1D6FC})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD}^{\frac{2N}{N+1}})^{-m}\frac{2^{2m(N-1)}}{N}\biggl(\frac{1}{2}\unicode[STIX]{x1D701}(2m+1)+(-1)^{\frac{N+3}{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}}{\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{m+\frac{N+3}{2}}2^{2Nm}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}+m\rfloor }\frac{(-1)^{j}B_{2j}B_{N+1+2N(m-j)}}{(2j)!(N+1+2N(m-j))!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)}{N+1}}.\end{eqnarray}$$In [Reference Kanemitsu, Tanigawa and Yoshimoto37, Theorem 2.1], Kanemitsu et al. studied the more general series
and obtained a nice transformation for it when ![]() $0<a\leqslant 1$,
$0<a\leqslant 1$, ![]() $h\geqslant N/2$ and
$h\geqslant N/2$ and ![]() $N$ even,Footnote 1 which can be conceived of as a formula for the Hurwitz zeta function
$N$ even,Footnote 1 which can be conceived of as a formula for the Hurwitz zeta function ![]() $\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)$. In the same paper, the trio also obtained a similar result for multiple Hurwitz zeta function [Reference Kanemitsu, Tanigawa and Yoshimoto37, Theorem 4.1].
$\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)$. In the same paper, the trio also obtained a similar result for multiple Hurwitz zeta function [Reference Kanemitsu, Tanigawa and Yoshimoto37, Theorem 4.1].
In the current paper, we derive a transformation for the series in (1.3) for any positive integer ![]() $N$. This transformation can be conceived of as a formula for
$N$. This transformation can be conceived of as a formula for ![]() $\unicode[STIX]{x1D701}(\frac{b}{c},a)$, when
$\unicode[STIX]{x1D701}(\frac{b}{c},a)$, when ![]() $b$ is odd and
$b$ is odd and ![]() $c$ is a positive even integer, or when
$c$ is a positive even integer, or when ![]() $b$ is even and
$b$ is even and ![]() $c$ is a positive odd integer. In the case when
$c$ is a positive odd integer. In the case when ![]() $N$ is even and
$N$ is even and ![]() $h\geqslant N/2$, our result, though different in appearance, is equivalent to that of Kanemitsu, Tanigawa and Yoshimoto [Reference Kanemitsu, Tanigawa and Yoshimoto37, Theorem 2.1]. However, we extend it to include the case
$h\geqslant N/2$, our result, though different in appearance, is equivalent to that of Kanemitsu, Tanigawa and Yoshimoto [Reference Kanemitsu, Tanigawa and Yoshimoto37, Theorem 2.1]. However, we extend it to include the case ![]() $h<N/2$ too. Also, in the special case
$h<N/2$ too. Also, in the special case ![]() $a=1$ of (1.3) that was considered in [Reference Dixit and Maji21], it was demonstrated that one obtains more interesting results when
$a=1$ of (1.3) that was considered in [Reference Dixit and Maji21], it was demonstrated that one obtains more interesting results when ![]() $N$ is odd. Here too, the same phenomenon is observed for
$N$ is odd. Here too, the same phenomenon is observed for ![]() $0<a\leqslant 1$ in general. A transformation of (1.3) for
$0<a\leqslant 1$ in general. A transformation of (1.3) for ![]() $N$ odd and
$N$ odd and ![]() $h\geqslant 0$ is derived for the first time in this paper. It not only involves the generalized Lambert series with coefficients as trigonometric functions but also contains a new construct, which is an infinite series consisting of
$h\geqslant 0$ is derived for the first time in this paper. It not only involves the generalized Lambert series with coefficients as trigonometric functions but also contains a new construct, which is an infinite series consisting of ![]() $\unicode[STIX]{x1D713}(z)$, the logarithmic derivative of the gamma function
$\unicode[STIX]{x1D713}(z)$, the logarithmic derivative of the gamma function ![]() $\unicode[STIX]{x1D6E4}(z)$, and a logarithm.
$\unicode[STIX]{x1D6E4}(z)$, and a logarithm.
Two of the main theorems of our paper, namely Theorems 2.1 and 2.3, which give the transformation for the series in (1.3) for any positive integer ![]() $N$ and
$N$ and ![]() $h\geqslant N/2$, are presented below. These are followed by Theorem 2.4, which is equivalent to Theorem 2.3, and which gives a beautiful two-parameter generalization of Ramanujan’s formula for
$h\geqslant N/2$, are presented below. These are followed by Theorem 2.4, which is equivalent to Theorem 2.3, and which gives a beautiful two-parameter generalization of Ramanujan’s formula for ![]() $\unicode[STIX]{x1D701}(2m+1)$, that is (1.1), in the case
$\unicode[STIX]{x1D701}(2m+1)$, that is (1.1), in the case ![]() $m>0$. The nice thing about these results is that they are totally explicit, and the expression other than the residual terms, that is
$m>0$. The nice thing about these results is that they are totally explicit, and the expression other than the residual terms, that is ![]() $S(x,a)$ (see Equations (2.3) and (2.4)), is written in the form where one of the inner expressions involves only
$S(x,a)$ (see Equations (2.3) and (2.4)), is written in the form where one of the inner expressions involves only ![]() $\cos (2\unicode[STIX]{x1D70B}na)$ and the other, only
$\cos (2\unicode[STIX]{x1D70B}na)$ and the other, only ![]() $\sin (2\unicode[STIX]{x1D70B}na)$. This allows us to recover the results in [Reference Dixit and Maji21] as corollaries since for
$\sin (2\unicode[STIX]{x1D70B}na)$. This allows us to recover the results in [Reference Dixit and Maji21] as corollaries since for ![]() $a=1$, the expression involving
$a=1$, the expression involving ![]() $\sin (2\unicode[STIX]{x1D70B}na)$ simply vanishes. Such an expression is also reminiscent of Hurwitz’s formula [Reference Davenport18, page 72], namely, for
$\sin (2\unicode[STIX]{x1D70B}na)$ simply vanishes. Such an expression is also reminiscent of Hurwitz’s formula [Reference Davenport18, page 72], namely, for ![]() $\text{Re}(s)<0$ and
$\text{Re}(s)<0$ and ![]() $0<a\leqslant 1$,
$0<a\leqslant 1$,
It is also valid for ![]() $\text{Re}(s)<1$ provided
$\text{Re}(s)<1$ provided ![]() $a\neq 1$. Indeed, Hurwitz’s formula will play an important role in the proofs of our theorems.
$a\neq 1$. Indeed, Hurwitz’s formula will play an important role in the proofs of our theorems.
2 Main results
Theorem 2.1. Let ![]() $N$ be a positive integer and
$N$ be a positive integer and ![]() $h$ be an integer such that
$h$ be an integer such that ![]() $h\geqslant N/2$. Let
$h\geqslant N/2$. Let ![]() $x>0$ and
$x>0$ and ![]() $0<a\leqslant 1$. Let
$0<a\leqslant 1$. Let ![]() $A_{N,j}(y):=\unicode[STIX]{x1D70B}(2\unicode[STIX]{x1D70B}y)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\!$. If
$A_{N,j}(y):=\unicode[STIX]{x1D70B}(2\unicode[STIX]{x1D70B}y)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\!$. If ![]() $\frac{N-2h+1}{N}\neq -2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, then
$\frac{N-2h+1}{N}\neq -2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, then
where
 $$\begin{eqnarray}\displaystyle P(x,a) & := & \displaystyle -\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h)+\frac{\unicode[STIX]{x1D701}(2h)}{x}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{N-2h+1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{N-2h+1}{N},a\biggr)x^{-\frac{(N-2h+1)}{N}}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2h-(2j+1)N)x^{2j}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{h+1}}{2}(2\unicode[STIX]{x1D70B})^{2h}\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{2h-2jN}}{(2j)!(2h-2jN)!}x^{2j-1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(x,a) & := & \displaystyle -\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h)+\frac{\unicode[STIX]{x1D701}(2h)}{x}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{N-2h+1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{N-2h+1}{N},a\biggr)x^{-\frac{(N-2h+1)}{N}}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2h-(2j+1)N)x^{2j}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{h+1}}{2}(2\unicode[STIX]{x1D70B})^{2h}\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{2h-2jN}}{(2j)!(2h-2jN)!}x^{2j-1},\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle S(x,a) & := & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j}(\frac{n}{x}))-1)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\biggl[\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\biggr]\bigg\}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(x,a) & := & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j}(\frac{n}{x}))-1)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\biggl[\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\biggr]\bigg\}\end{eqnarray}$$ for ![]() $N$ odd, and
$N$ odd, and
 $$\begin{eqnarray}\displaystyle S(x,a) & := & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)(j+\frac{1}{2})}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+\frac{N}{2}+1}\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j+\frac{1}{2}}(\frac{n}{x}))-1)}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(x,a) & := & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)(j+\frac{1}{2})}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+\frac{N}{2}+1}\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j+\frac{1}{2}}(\frac{n}{x}))-1)}\end{eqnarray}$$ for ![]() $N$ even.
$N$ even.
Remark 1. Note that the above theorem does not hold for ![]() $N=1$.
$N=1$.
Remark 2. The above theorem can be conceived of as a formula of the Hurwitz zeta function ![]() $\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)$. When
$\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)$. When ![]() $a>1$, one can still obtain a representation from the above theorem. We consider two cases depending upon whether
$a>1$, one can still obtain a representation from the above theorem. We consider two cases depending upon whether ![]() $a$ is an integer or not. If
$a$ is an integer or not. If ![]() $a>1,a\notin \mathbb{Z}$, we apply Theorem 2.1 with
$a>1,a\notin \mathbb{Z}$, we apply Theorem 2.1 with ![]() $a$ replaced by its fractional part
$a$ replaced by its fractional part ![]() $\{a\}$ and then using the fact that
$\{a\}$ and then using the fact that ![]() $\unicode[STIX]{x1D701}(s,\{a\})=\unicode[STIX]{x1D701}(s,a)+\sum _{\ell =1}^{\lfloor a\rfloor }(\ell +\{a\}-1)^{-s}$. Now if
$\unicode[STIX]{x1D701}(s,\{a\})=\unicode[STIX]{x1D701}(s,a)+\sum _{\ell =1}^{\lfloor a\rfloor }(\ell +\{a\}-1)^{-s}$. Now if ![]() $a>1,a\in \mathbb{Z}$, we can use Theorem 2.1 with
$a>1,a\in \mathbb{Z}$, we can use Theorem 2.1 with ![]() $a$there to be
$a$there to be ![]() $1$, and then the identity
$1$, and then the identity ![]() $\unicode[STIX]{x1D701}(s)=\unicode[STIX]{x1D701}(s,a)+\sum _{\ell =1}^{a-1}\ell ^{-s}$. The above identities are easily seen to be true for
$\unicode[STIX]{x1D701}(s)=\unicode[STIX]{x1D701}(s,a)+\sum _{\ell =1}^{a-1}\ell ^{-s}$. The above identities are easily seen to be true for ![]() $\text{Re}(s)>1$ first, and then for all
$\text{Re}(s)>1$ first, and then for all ![]() $s\in \mathbb{C}$ by analytic continuation.
$s\in \mathbb{C}$ by analytic continuation.
An important ingredient in the proof of Theorem 2.1 is a new identity which gives a closed-form expression for an infinite sum whose summand is Raabe’s cosine transform ![]() $\mathfrak{R}(y,w)$. For
$\mathfrak{R}(y,w)$. For ![]() $\text{Re}(w)>0$ and
$\text{Re}(w)>0$ and ![]() $y>0$, the latter is given by [Reference Erdélyi, Magnus, Oberhettinger and Tricomi24, page 144]
$y>0$, the latter is given by [Reference Erdélyi, Magnus, Oberhettinger and Tricomi24, page 144]
where it is termed as one of the two Raabe’s integrals. However, the integral ![]() $\int _{0}^{1}\log \unicode[STIX]{x1D6E4}(t)\text{d}t$ is more popularly known as Raabe’s integral. Hence to avoid any confusion, we call the integral in (2.5) as Raabe’s cosine transform.
$\int _{0}^{1}\log \unicode[STIX]{x1D6E4}(t)\text{d}t$ is more popularly known as Raabe’s integral. Hence to avoid any confusion, we call the integral in (2.5) as Raabe’s cosine transform.
The aforementioned identity on infinite series of Raabe’s cosine transform which is interesting in itself, and to the best of our knowledge is new, is now given.
Theorem 2.2. Let ![]() $u\in \mathbb{C}$ be fixed such that
$u\in \mathbb{C}$ be fixed such that ![]() $\text{Re}(u)>0$. Then,
$\text{Re}(u)>0$. Then,
The series on the left-hand side of this result is not amenable to a straightforward evaluation and hence to obtain the result we had to use Guinand’s generalization of the Poisson summation formula [Reference Guinand30, Theorem 1]. Note that interchanging the order of summation and integration leads to a divergent integral. It is interesting to note that while Raabe’s cosine transform itself is evaluable in terms of, either the exponential integral function [Reference Erdélyi, Magnus, Oberhettinger and Tricomi24, page 144, Equation (13)], [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 428, Formula 3.723.5] or, equivalently, ![]() $\text{Shi}(x)$ and
$\text{Shi}(x)$ and ![]() $\text{Chi}(x)$ functions [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 895, Formulas 8.221.1, 8.221.2], which are not-so-common special functions, the infinite sum of Raabe’s cosine transform can be expressed in terms of well-known functions, namely, the digamma function
$\text{Chi}(x)$ functions [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 895, Formulas 8.221.1, 8.221.2], which are not-so-common special functions, the infinite sum of Raabe’s cosine transform can be expressed in terms of well-known functions, namely, the digamma function ![]() $\unicode[STIX]{x1D713}(z)$ and
$\unicode[STIX]{x1D713}(z)$ and ![]() $\log (z)$.
$\log (z)$.
A complement of Theorem 2.1 is stated next.
Theorem 2.3. Let ![]() $\unicode[STIX]{x1D6FE}$ denote Euler’s constant. Let
$\unicode[STIX]{x1D6FE}$ denote Euler’s constant. Let ![]() $0<a\leqslant 1$. Let
$0<a\leqslant 1$. Let ![]() $N$ be an odd positive integer and
$N$ be an odd positive integer and ![]() $h$ be an integer such that
$h$ be an integer such that ![]() $h>N/2$. Let
$h>N/2$. Let ![]() $A_{N,j}(y)$ be defined as in Theorem 2.1. If
$A_{N,j}(y)$ be defined as in Theorem 2.1. If ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \neq 0$, then
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \neq 0$, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}\nonumber\\ \displaystyle & & \displaystyle \quad =-\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h)-\unicode[STIX]{x1D6FE}\frac{B_{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}(a)}{(2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor )!}x^{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\frac{(-1)^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }}{2N}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor -1}\frac{B_{2j+1}(a)}{(2j+1)!}\frac{\unicode[STIX]{x1D701}(2h-(2j+1)N)}{x^{-2j}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{h+1}(2\unicode[STIX]{x1D70B})^{2h}}{2}\mathop{\sum }_{j=0}^{\lfloor \frac{h}{N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{2h-2jN}}{(2j)!(2h-2jN)!}x^{2j-1}+\frac{(-1)^{h+1}}{N}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j}(\frac{n}{x}))-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+3}{2}}}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\bigg\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}\nonumber\\ \displaystyle & & \displaystyle \quad =-\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h)-\unicode[STIX]{x1D6FE}\frac{B_{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}(a)}{(2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor )!}x^{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\frac{(-1)^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }}{2N}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor -1}\frac{B_{2j+1}(a)}{(2j+1)!}\frac{\unicode[STIX]{x1D701}(2h-(2j+1)N)}{x^{-2j}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{h+1}(2\unicode[STIX]{x1D70B})^{2h}}{2}\mathop{\sum }_{j=0}^{\lfloor \frac{h}{N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{2h-2jN}}{(2j)!(2h-2jN)!}x^{2j-1}+\frac{(-1)^{h+1}}{N}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j}(\frac{n}{x}))-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+3}{2}}}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\bigg\}.\end{eqnarray}$$Remark 3. An equivalent version of Theorem 2.3, comparable in appearance to Theorem 2.1, is given in (5.2).
One difference in the hypotheses of Theorems 2.1 and 2.3, in the case when ![]() $N$ is an odd positive integer is that, in the first, we have
$N$ is an odd positive integer is that, in the first, we have ![]() $\frac{N-2h+1}{N}\neq -2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, whereas in the second,
$\frac{N-2h+1}{N}\neq -2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, whereas in the second, ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \neq 0$. (The remaining case
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \neq 0$. (The remaining case ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$ is covered in Theorem 2.7.) Note that the equality
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$ is covered in Theorem 2.7.) Note that the equality ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ does not hold for any even
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ does not hold for any even ![]() $N$, but it may very well hold for some specific values of
$N$, but it may very well hold for some specific values of ![]() $N$ odd and
$N$ odd and ![]() $h$. Even though at a first glance, these conditions may look artificial, as will be seen in the proofs, they arise naturally while examining the poles of
$h$. Even though at a first glance, these conditions may look artificial, as will be seen in the proofs, they arise naturally while examining the poles of ![]() $\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))x^{-s}$, which is the integrand of the line integral representation of
$\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))x^{-s}$, which is the integrand of the line integral representation of ![]() $\sum _{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}$ (see (4.4)). So if we now consider the poles of
$\sum _{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}$ (see (4.4)). So if we now consider the poles of ![]() $\unicode[STIX]{x1D6E4}(s)$ at
$\unicode[STIX]{x1D6E4}(s)$ at ![]() $-2,-4,-6,\ldots ,$ they get canceled by the zeros of
$-2,-4,-6,\ldots ,$ they get canceled by the zeros of ![]() $\unicode[STIX]{x1D701}(s,a)$only when
$\unicode[STIX]{x1D701}(s,a)$only when ![]() $a=1$ or
$a=1$ or ![]() $a=\frac{1}{2}$, for then
$a=\frac{1}{2}$, for then ![]() $\unicode[STIX]{x1D701}(s,1)=\unicode[STIX]{x1D701}(s)$ and
$\unicode[STIX]{x1D701}(s,1)=\unicode[STIX]{x1D701}(s)$ and ![]() $\unicode[STIX]{x1D701}(s,\frac{1}{2})=(2^{s}-1)\unicode[STIX]{x1D701}(s)$, and it is well known that
$\unicode[STIX]{x1D701}(s,\frac{1}{2})=(2^{s}-1)\unicode[STIX]{x1D701}(s)$, and it is well known that ![]() $\unicode[STIX]{x1D701}(-2m)=0$ for
$\unicode[STIX]{x1D701}(-2m)=0$ for ![]() $m\geqslant 1$. However, for
$m\geqslant 1$. However, for ![]() $0<a<1,a\neq \frac{1}{2}$,
$0<a<1,a\neq \frac{1}{2}$, ![]() $\unicode[STIX]{x1D701}(-2m,a),m\geqslant 1$, may not always be zero.
$\unicode[STIX]{x1D701}(-2m,a),m\geqslant 1$, may not always be zero.
In fact, a theorem due to Spira [Reference Spira59, Theorem 3] states that if ![]() $\text{Re}(s)\leqslant -(4a+1+2\lfloor 1-2a\rfloor )$ and
$\text{Re}(s)\leqslant -(4a+1+2\lfloor 1-2a\rfloor )$ and ![]() $|\text{Im}(s)|\leqslant 1$, then
$|\text{Im}(s)|\leqslant 1$, then ![]() $\unicode[STIX]{x1D701}(s,a)\neq 0$ except for trivial zeros on the negative real axis, one in each interval
$\unicode[STIX]{x1D701}(s,a)\neq 0$ except for trivial zeros on the negative real axis, one in each interval ![]() $(-2n-4a-1,-2n-4a+1)$, where
$(-2n-4a-1,-2n-4a+1)$, where ![]() $n\geqslant 1-2a$. Thus, some (or all) of the poles of
$n\geqslant 1-2a$. Thus, some (or all) of the poles of ![]() $\unicode[STIX]{x1D6E4}(s)$ at
$\unicode[STIX]{x1D6E4}(s)$ at ![]() $s=-2m,m\geqslant 1$, may very well contribute nonzero residues toward the evaluation of the line integral. Now
$s=-2m,m\geqslant 1$, may very well contribute nonzero residues toward the evaluation of the line integral. Now ![]() $h\geqslant N/2$ implies that
$h\geqslant N/2$ implies that ![]() $\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \geqslant 0$. First consider
$\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \geqslant 0$. First consider ![]() $\lfloor \frac{h}{N}-\frac{1}{2}\rfloor >0$ so that
$\lfloor \frac{h}{N}-\frac{1}{2}\rfloor >0$ so that ![]() $-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ is a legitimate pole of
$-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ is a legitimate pole of ![]() $\unicode[STIX]{x1D6E4}(s)$. If, in addition, we have
$\unicode[STIX]{x1D6E4}(s)$. If, in addition, we have ![]() $\frac{N-2h+1}{N}=-2j$ for some
$\frac{N-2h+1}{N}=-2j$ for some ![]() $j\in \mathbb{N}$, then Lemma 4.2 implies that
$j\in \mathbb{N}$, then Lemma 4.2 implies that ![]() $j=\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$. Now since
$j=\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$. Now since ![]() $\frac{N-2h+1}{N}$ is the pole of
$\frac{N-2h+1}{N}$ is the pole of ![]() $\unicode[STIX]{x1D701}(\!Ns-(N-2h))$, we find that this is a double order pole of the integrand in (4.4). This is why
$\unicode[STIX]{x1D701}(\!Ns-(N-2h))$, we find that this is a double order pole of the integrand in (4.4). This is why ![]() $P(x,a)$ in Theorem 2.1 gets modified to
$P(x,a)$ in Theorem 2.1 gets modified to ![]() $P^{\ast }(x,a)$ as can be seen in (5.2), which is an equivalent version of Theorem 2.3.
$P^{\ast }(x,a)$ as can be seen in (5.2), which is an equivalent version of Theorem 2.3.
The aforementioned fact about ![]() $\unicode[STIX]{x1D701}(s,a)$ not always having zeros at
$\unicode[STIX]{x1D701}(s,a)$ not always having zeros at ![]() $s=-2m,m\in \mathbb{N}$, for
$s=-2m,m\in \mathbb{N}$, for ![]() $0<a<1$ suggests that we write down the important differences between
$0<a<1$ suggests that we write down the important differences between ![]() $\unicode[STIX]{x1D701}(s,a)$ and
$\unicode[STIX]{x1D701}(s,a)$ and ![]() $\unicode[STIX]{x1D701}(s)$. For the remainder of this paragraph, assume
$\unicode[STIX]{x1D701}(s)$. For the remainder of this paragraph, assume ![]() $0<a<1$ with
$0<a<1$ with ![]() $a\neq \frac{1}{2}$. Then unlike
$a\neq \frac{1}{2}$. Then unlike ![]() $\unicode[STIX]{x1D701}(s)$,
$\unicode[STIX]{x1D701}(s)$, ![]() $\unicode[STIX]{x1D701}(s,a)$ has no Euler product. It is known, due to Davenport and Heilbronn [Reference Davenport and Heilbronn19] in the case when
$\unicode[STIX]{x1D701}(s,a)$ has no Euler product. It is known, due to Davenport and Heilbronn [Reference Davenport and Heilbronn19] in the case when ![]() $a$ is rational or transcendental, and due to Cassels [Reference Cassels16] in the case when
$a$ is rational or transcendental, and due to Cassels [Reference Cassels16] in the case when ![]() $a$ is algebraic irrational, that
$a$ is algebraic irrational, that ![]() $\unicode[STIX]{x1D701}(s,a)$ has infinitely many zeros in the half-plane
$\unicode[STIX]{x1D701}(s,a)$ has infinitely many zeros in the half-plane ![]() $\text{Re}(s)>1$. Moreover, for
$\text{Re}(s)>1$. Moreover, for ![]() $a$ rational, Voronin [Reference Voronin65] proved that
$a$ rational, Voronin [Reference Voronin65] proved that ![]() $\unicode[STIX]{x1D701}(s,a)$ has infinitely many zeros in the region
$\unicode[STIX]{x1D701}(s,a)$ has infinitely many zeros in the region ![]() $\frac{1}{2}<\text{Re}(s)<1$. The corresponding result when
$\frac{1}{2}<\text{Re}(s)<1$. The corresponding result when ![]() $a$ is transcendental was obtained by Gonek [Reference Gonek31].
$a$ is transcendental was obtained by Gonek [Reference Gonek31].
We now give an equivalent version of Theorem 2.3, which, for ![]() $m>0$, gives an amazing two-parameter generalization of Ramanujan’s formula (1.1) relating the cosine Dirichlet series at odd integers, that is
$m>0$, gives an amazing two-parameter generalization of Ramanujan’s formula (1.1) relating the cosine Dirichlet series at odd integers, that is ![]() $\sum _{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}$, with the odd zeta values
$\sum _{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}$, with the odd zeta values ![]() $\unicode[STIX]{x1D701}(2Nm+1-2jN),0\leqslant j\leqslant m-1$.
$\unicode[STIX]{x1D701}(2Nm+1-2jN),0\leqslant j\leqslant m-1$.
Theorem 2.4. Let ![]() $0<a\leqslant 1$, let
$0<a\leqslant 1$, let ![]() $N$ be an odd positive integer and
$N$ be an odd positive integer and ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$. Then for any positive integer
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$. Then for any positive integer ![]() $m$,
$m$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-\frac{2Nm}{N+1}}\biggl(\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(2Nm+1)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{j=1}^{m-1}\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2Nm+1-2jN)(2^{N}\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm-1}\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD}^{\frac{2N}{N+1}})^{-m}\frac{2^{2m(N-1)}}{N}\biggl[\frac{(-1)^{m+1}(2\unicode[STIX]{x1D70B})^{2m}B_{2m+1}(a)N\unicode[STIX]{x1D6FE}}{(2m+1)!}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}\cos (2\unicode[STIX]{x1D70B}na)}{\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+3}{2}}}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D713}\biggl(\frac{-i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}\biggr]+2^{2Nm}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(-1)^{m+\frac{N+3}{2}}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}+m\rfloor }\frac{(-1)^{j}B_{2j}(a)B_{N+1+2N(m-j)}}{(2j)!(N+1+2N(m-j))!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)}{N+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-\frac{2Nm}{N+1}}\biggl(\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(2Nm+1)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{j=1}^{m-1}\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2Nm+1-2jN)(2^{N}\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm-1}\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD}^{\frac{2N}{N+1}})^{-m}\frac{2^{2m(N-1)}}{N}\biggl[\frac{(-1)^{m+1}(2\unicode[STIX]{x1D70B})^{2m}B_{2m+1}(a)N\unicode[STIX]{x1D6FE}}{(2m+1)!}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}\cos (2\unicode[STIX]{x1D70B}na)}{\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+3}{2}}}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D713}\biggl(\frac{-i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}\biggr]+2^{2Nm}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(-1)^{m+\frac{N+3}{2}}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}+m\rfloor }\frac{(-1)^{j}B_{2j}(a)B_{N+1+2N(m-j)}}{(2j)!(N+1+2N(m-j))!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)}{N+1}}.\end{eqnarray}$$ When we let ![]() $a=1$ in the above theorem, we obtain (1.2) for positive integers
$a=1$ in the above theorem, we obtain (1.2) for positive integers ![]() $m$, which, in turn, for
$m$, which, in turn, for ![]() $N=1$, gives Ramanujan’s formula (1.1) for
$N=1$, gives Ramanujan’s formula (1.1) for ![]() $m>0$ as its special case.
$m>0$ as its special case.
The importance of the above theorem is now explained. Berndt [Reference Berndt7] proved that Euler’s formula [Reference Temme61, page 5, Equation (1.14)]
and Ramanujan’s formula (1.1) are natural companions since both turn out to be special cases of his general theorem [Reference Berndt7, Theorem 2.2]. A generalization of (2.9) is [Reference Temme61, page 5]
Then an obvious question that comes to our mind is, does there exist a natural companion of (2.10) which involves ![]() $\sum _{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}$? While this might be answerable only if a generalization of Berndt’s [Reference Berndt7, Theorem 2.2] exists, the best candidate that we offer here is Theorem 2.4 or its
$\sum _{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}$? While this might be answerable only if a generalization of Berndt’s [Reference Berndt7, Theorem 2.2] exists, the best candidate that we offer here is Theorem 2.4 or its ![]() $N=1$ case, that is, Theorem 5.2.
$N=1$ case, that is, Theorem 5.2.
Theorem 2.4 gives the following beautiful formula relating ![]() $\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5)$,
$\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5)$, ![]() $\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ and
$\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ and ![]() $\unicode[STIX]{x1D701}(11)$, which might be explored from the point of view of numerical computations.
$\unicode[STIX]{x1D701}(11)$, which might be explored from the point of view of numerical computations.
Corollary 2.5. The following identity holds:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{277}{8257536}\frac{\unicode[STIX]{x1D701}(3)}{\unicode[STIX]{x1D70B}^{3}}-\frac{61}{184320}\frac{\unicode[STIX]{x1D701}(5)}{\unicode[STIX]{x1D70B}^{5}}+\frac{5}{1536}\frac{\unicode[STIX]{x1D701}(7)}{\unicode[STIX]{x1D70B}^{7}}-\frac{1}{32}\frac{\unicode[STIX]{x1D701}(9)}{\unicode[STIX]{x1D70B}^{9}}+\frac{1049599}{4194304}\frac{\unicode[STIX]{x1D701}(11)}{\unicode[STIX]{x1D70B}^{11}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1315686689}{3570822807552000}-\frac{50521}{14863564800}\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{\unicode[STIX]{x1D70B}^{11}}\mathop{\sum }_{n=1}^{\infty }\frac{e^{3\unicode[STIX]{x1D70B}n/2}}{n^{11}(e^{2\unicode[STIX]{x1D70B}n}-1)}+\frac{1}{2048\unicode[STIX]{x1D70B}^{11}}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}}{n^{11}(e^{4\unicode[STIX]{x1D70B}n}-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2\unicode[STIX]{x1D70B}^{12}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (\frac{\unicode[STIX]{x1D70B}n}{2})}{n^{11}}(\unicode[STIX]{x1D713}(in)+\unicode[STIX]{x1D713}(-in)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{277}{8257536}\frac{\unicode[STIX]{x1D701}(3)}{\unicode[STIX]{x1D70B}^{3}}-\frac{61}{184320}\frac{\unicode[STIX]{x1D701}(5)}{\unicode[STIX]{x1D70B}^{5}}+\frac{5}{1536}\frac{\unicode[STIX]{x1D701}(7)}{\unicode[STIX]{x1D70B}^{7}}-\frac{1}{32}\frac{\unicode[STIX]{x1D701}(9)}{\unicode[STIX]{x1D70B}^{9}}+\frac{1049599}{4194304}\frac{\unicode[STIX]{x1D701}(11)}{\unicode[STIX]{x1D70B}^{11}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1315686689}{3570822807552000}-\frac{50521}{14863564800}\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{\unicode[STIX]{x1D70B}^{11}}\mathop{\sum }_{n=1}^{\infty }\frac{e^{3\unicode[STIX]{x1D70B}n/2}}{n^{11}(e^{2\unicode[STIX]{x1D70B}n}-1)}+\frac{1}{2048\unicode[STIX]{x1D70B}^{11}}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}}{n^{11}(e^{4\unicode[STIX]{x1D70B}n}-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2\unicode[STIX]{x1D70B}^{12}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (\frac{\unicode[STIX]{x1D70B}n}{2})}{n^{11}}(\unicode[STIX]{x1D713}(in)+\unicode[STIX]{x1D713}(-in)).\nonumber\end{eqnarray}$$ It should be noted that there are formulas of other type linking ![]() $\unicode[STIX]{x1D701}(3),\ldots ,\unicode[STIX]{x1D701}(2m+1)$ discovered, for example, by Wilton [Reference Wilton68], by Srivastava [Reference Srivastava60] (see also the references therein), and by Kanemitsu et. al. [Reference Kanemitsu, Tanigawa and Yoshimoto36]. For details, refer to [Reference Kanemitsu, Tanigawa and Yoshimoto36]. However, the advantage of Theorem 2.4 lies in the fact that one can vary
$\unicode[STIX]{x1D701}(3),\ldots ,\unicode[STIX]{x1D701}(2m+1)$ discovered, for example, by Wilton [Reference Wilton68], by Srivastava [Reference Srivastava60] (see also the references therein), and by Kanemitsu et. al. [Reference Kanemitsu, Tanigawa and Yoshimoto36]. For details, refer to [Reference Kanemitsu, Tanigawa and Yoshimoto36]. However, the advantage of Theorem 2.4 lies in the fact that one can vary ![]() $N$ over the set of odd positive integers, and hence it allows us to obtain a relation between odd zeta values
$N$ over the set of odd positive integers, and hence it allows us to obtain a relation between odd zeta values ![]() $\unicode[STIX]{x1D701}(2N+1),\unicode[STIX]{x1D701}(4N+1),\unicode[STIX]{x1D701}(6N+1),\ldots ,\unicode[STIX]{x1D701}(2Nm+1)$.
$\unicode[STIX]{x1D701}(2N+1),\unicode[STIX]{x1D701}(4N+1),\unicode[STIX]{x1D701}(6N+1),\ldots ,\unicode[STIX]{x1D701}(2Nm+1)$.
Note that (2.9) implies that ![]() $\unicode[STIX]{x1D701}(2m)$ is transcendental for every
$\unicode[STIX]{x1D701}(2m)$ is transcendental for every ![]() $m\in \mathbb{N}$. However, the arithmetical nature of
$m\in \mathbb{N}$. However, the arithmetical nature of ![]() $\unicode[STIX]{x1D701}(2m+1)$ is quite mysterious. It is widely believed [Reference Waldschmidt66, Conjecture 27] that for any
$\unicode[STIX]{x1D701}(2m+1)$ is quite mysterious. It is widely believed [Reference Waldschmidt66, Conjecture 27] that for any ![]() $n\in \mathbb{N}$, and any nonzero polynomial
$n\in \mathbb{N}$, and any nonzero polynomial ![]() $P\in \mathbb{Q}[x_{0},x_{1},\ldots ,x_{n}]$,
$P\in \mathbb{Q}[x_{0},x_{1},\ldots ,x_{n}]$, ![]() $P(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(2n+1))\neq 0$, that is,
$P(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\ldots ,\unicode[STIX]{x1D701}(2n+1))\neq 0$, that is, ![]() $\unicode[STIX]{x1D70B}$ and all odd zeta values are algebraically independent over
$\unicode[STIX]{x1D70B}$ and all odd zeta values are algebraically independent over ![]() $\mathbb{Q}$. This conjecture, if true, would imply, in particular, that all odd zeta values are transcendental. While this is not known as of yet for even a single odd zeta value
$\mathbb{Q}$. This conjecture, if true, would imply, in particular, that all odd zeta values are transcendental. While this is not known as of yet for even a single odd zeta value ![]() $\unicode[STIX]{x1D701}(2m+1),m>0$, Apéry [Reference Apéry2], [Reference Apéry3] proved that
$\unicode[STIX]{x1D701}(2m+1),m>0$, Apéry [Reference Apéry2], [Reference Apéry3] proved that ![]() $\unicode[STIX]{x1D701}(3)$ is irrational. Also, Rivoal [Reference Rivoal57], and Ball and Rivoal [Reference Ball and Rivoal6] have proved that there exist infinitely many odd zeta values which are irrational. However, one does not know which out of these odd zeta values (except
$\unicode[STIX]{x1D701}(3)$ is irrational. Also, Rivoal [Reference Rivoal57], and Ball and Rivoal [Reference Ball and Rivoal6] have proved that there exist infinitely many odd zeta values which are irrational. However, one does not know which out of these odd zeta values (except ![]() $\unicode[STIX]{x1D701}(3)$) are irrational. Currently the best result in this direction is due to Zudilin [Reference Zudilin69] which says that at least one of
$\unicode[STIX]{x1D701}(3)$) are irrational. Currently the best result in this direction is due to Zudilin [Reference Zudilin69] which says that at least one of ![]() $\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ or
$\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ or ![]() $\unicode[STIX]{x1D701}(11)$ is irrational. Hence results of the type as Corollary 2.5 are welcome for they may shed some light on these outstanding open questions. Very recently Hančl and Kristensen [Reference Hančl and Kristensen33] have obtained criteria for irrationality of odd zeta values and Euler’s constant.
$\unicode[STIX]{x1D701}(11)$ is irrational. Hence results of the type as Corollary 2.5 are welcome for they may shed some light on these outstanding open questions. Very recently Hančl and Kristensen [Reference Hančl and Kristensen33] have obtained criteria for irrationality of odd zeta values and Euler’s constant.
Theorem 2.4 allows us to deduce a new elegant formula for ![]() $\unicode[STIX]{x1D701}(2m+1)$.
$\unicode[STIX]{x1D701}(2m+1)$.
Theorem 2.6. Let ![]() $N$ be an odd positive integer and
$N$ be an odd positive integer and ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$. Then for any positive integer
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$. Then for any positive integer ![]() $m$,
$m$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-\frac{2Nm}{N+1}}\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm-1}\text{exp}(-\frac{1}{2}(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC})}\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD}^{\frac{2N}{N+1}})^{-m}\frac{2^{2m(N-1)}}{N}\biggl[\frac{(2^{-2m}-1)}{2}\unicode[STIX]{x1D701}(2m+1)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}n^{-2m-1}}{\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1}\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{m+\frac{N+3}{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,2^{2Nm}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}+m\rfloor }\frac{(-1)^{j}(2^{1-2j}-1)B_{2j}B_{N+1+2N(m-j)}}{(2j)!(N+1+2N(m-j))!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)}{N+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-\frac{2Nm}{N+1}}\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm-1}\text{exp}(-\frac{1}{2}(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC})}\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD}^{\frac{2N}{N+1}})^{-m}\frac{2^{2m(N-1)}}{N}\biggl[\frac{(2^{-2m}-1)}{2}\unicode[STIX]{x1D701}(2m+1)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}n^{-2m-1}}{\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1}\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{m+\frac{N+3}{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,2^{2Nm}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}+m\rfloor }\frac{(-1)^{j}(2^{1-2j}-1)B_{2j}B_{N+1+2N(m-j)}}{(2j)!(N+1+2N(m-j))!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)}{N+1}}.\end{eqnarray}$$ We next derive a transformation for ![]() $\sum _{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}$ for
$\sum _{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}$ for ![]() $N$ odd and
$N$ odd and ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$, that is,
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$, that is, ![]() $h=\frac{N+1}{2}$, in terms of
$h=\frac{N+1}{2}$, in terms of ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FD}$, where
$\unicode[STIX]{x1D6FD}$, where ![]() $\unicode[STIX]{x1D6FC}=\frac{x}{2^{N}},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$.
$\unicode[STIX]{x1D6FC}=\frac{x}{2^{N}},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$.
Theorem 2.7. Let ![]() $0<a\leqslant 1$ and
$0<a\leqslant 1$ and ![]() $N$ be an odd positive integer. If
$N$ be an odd positive integer. If ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{n(1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC}))}-\frac{1}{N}(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n(\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1)}+\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \bigg\{\log \biggl(\frac{\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D713}\biggl(\frac{-i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{N}((a-1)\log (2\unicode[STIX]{x1D70B})+\log \unicode[STIX]{x1D6E4}(a))+\biggl(a-\frac{1}{2}\biggr)\bigg\{\frac{(N-1)(\log 2-\unicode[STIX]{x1D6FE})}{N}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\log (\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD})}{N+1}\bigg\}+(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}\rfloor }\frac{(-1)^{j}B_{2j}(a)B_{N+1-2Nj}}{(2j)!(N+1-2Nj)!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N-\frac{2N^{2}j}{N+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{n(1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC}))}-\frac{1}{N}(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n(\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1)}+\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \bigg\{\log \biggl(\frac{\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D713}\biggl(\frac{-i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{N}((a-1)\log (2\unicode[STIX]{x1D70B})+\log \unicode[STIX]{x1D6E4}(a))+\biggl(a-\frac{1}{2}\biggr)\bigg\{\frac{(N-1)(\log 2-\unicode[STIX]{x1D6FE})}{N}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\log (\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD})}{N+1}\bigg\}+(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}\rfloor }\frac{(-1)^{j}B_{2j}(a)B_{N+1-2Nj}}{(2j)!(N+1-2Nj)!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N-\frac{2N^{2}j}{N+1}}.\end{eqnarray}$$Remark 4. Note that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}\rfloor }\frac{(-1)^{j}B_{2j}(a)B_{N+1-2Nj}}{(2j)!(N+1-2Nj)!}\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N-\frac{2N^{2}j}{N+1}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}\displaystyle \!\frac{\unicode[STIX]{x1D6FD}}{12}-\frac{\unicode[STIX]{x1D6FC}}{2}\biggl(a^{2}-a+\frac{1}{6}\biggr)\quad & \text{if }N=1,\\ \displaystyle \!\frac{B_{N+1}\unicode[STIX]{x1D6FD}^{N}}{(N+1)!}\quad & \text{if }N>1.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}\rfloor }\frac{(-1)^{j}B_{2j}(a)B_{N+1-2Nj}}{(2j)!(N+1-2Nj)!}\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N-\frac{2N^{2}j}{N+1}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}\displaystyle \!\frac{\unicode[STIX]{x1D6FD}}{12}-\frac{\unicode[STIX]{x1D6FC}}{2}\biggl(a^{2}-a+\frac{1}{6}\biggr)\quad & \text{if }N=1,\\ \displaystyle \!\frac{B_{N+1}\unicode[STIX]{x1D6FD}^{N}}{(N+1)!}\quad & \text{if }N>1.\end{array}\right.\nonumber\end{eqnarray}$$ When ![]() $a=1$ in (2.12), one recovers Corollary 1.6 from [Reference Dixit and Maji21]. Further, if we let
$a=1$ in (2.12), one recovers Corollary 1.6 from [Reference Dixit and Maji21]. Further, if we let ![]() $N=1$, one obtains the well-known transformation formula for the logarithm of the Dedekind eta function [Reference Ramanujan55, Ch. 14, Section 8, Corollary (ii) and Ch. 16, Entry 27(iii)], [Reference Berndt8, page 256], [Reference Berndt9, page 43], [Reference Ramanujan56, page 320, Formula (29)]: For
$N=1$, one obtains the well-known transformation formula for the logarithm of the Dedekind eta function [Reference Ramanujan55, Ch. 14, Section 8, Corollary (ii) and Ch. 16, Entry 27(iii)], [Reference Berndt8, page 256], [Reference Berndt9, page 43], [Reference Ramanujan56, page 320, Formula (29)]: For ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ and ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$,
Note that the Dedekind eta function ![]() $\unicode[STIX]{x1D702}(z)$ is defined for
$\unicode[STIX]{x1D702}(z)$ is defined for ![]() $z\in \mathbb{H}$ (upper half-plane) by
$z\in \mathbb{H}$ (upper half-plane) by ![]() $\unicode[STIX]{x1D702}(z):=e^{2\unicode[STIX]{x1D70B}iz/24}\prod _{n=1}^{\infty }(1-e^{2\unicode[STIX]{x1D70B}inz})$, and satisfies the transformation formula [Reference Apostol4, page 48]
$\unicode[STIX]{x1D702}(z):=e^{2\unicode[STIX]{x1D70B}iz/24}\prod _{n=1}^{\infty }(1-e^{2\unicode[STIX]{x1D70B}inz})$, and satisfies the transformation formula [Reference Apostol4, page 48] ![]() $\unicode[STIX]{x1D702}(-\frac{1}{z})=\sqrt{-iz}\unicode[STIX]{x1D702}(z)$, which is equivalent to (2.13). Thus, Theorem 2.7 is a two-parameter generalization of the transformation formula for
$\unicode[STIX]{x1D702}(-\frac{1}{z})=\sqrt{-iz}\unicode[STIX]{x1D702}(z)$, which is equivalent to (2.13). Thus, Theorem 2.7 is a two-parameter generalization of the transformation formula for ![]() $\log \unicode[STIX]{x1D702}(z)$.
$\log \unicode[STIX]{x1D702}(z)$.
For ![]() $0<a<1$, a vastly simplified version of Theorem 2.7 given below can be obtained.
$0<a<1$, a vastly simplified version of Theorem 2.7 given below can be obtained.
Corollary 2.8. Let ![]() $0<a<1$ and
$0<a<1$ and ![]() $N$ be an odd positive integer. Then
$N$ be an odd positive integer. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{n(1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC}))}-\frac{1}{N}(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n(\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1)}+\frac{1}{2\unicode[STIX]{x1D70B}}(-1)^{j+\frac{N+3}{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FE}\biggl(\frac{1}{2}-a\biggr)-\frac{\log (2\sin (\unicode[STIX]{x1D70B}a))}{2N}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}\rfloor }\frac{(-1)^{j}B_{2j}(a)B_{N+1-2Nj}}{(2j)!(N+1-2Nj)!}\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N-\frac{2N^{2}j}{N+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{n(1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC}))}-\frac{1}{N}(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n(\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1)}+\frac{1}{2\unicode[STIX]{x1D70B}}(-1)^{j+\frac{N+3}{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FE}\biggl(\frac{1}{2}-a\biggr)-\frac{\log (2\sin (\unicode[STIX]{x1D70B}a))}{2N}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}\rfloor }\frac{(-1)^{j}B_{2j}(a)B_{N+1-2Nj}}{(2j)!(N+1-2Nj)!}\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N-\frac{2N^{2}j}{N+1}}.\end{eqnarray}$$ The additional parameter ![]() $a$ allows us to obtain new analogues of (2.13), for example, the following result. The other analogue is derived in Corollary 9.1.
$a$ allows us to obtain new analogues of (2.13), for example, the following result. The other analogue is derived in Corollary 9.1.
Corollary 2.9. For ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$,
An equivalent form is
which draws similarity with the transformation formula for ![]() $\unicode[STIX]{x1D702}(z)$.
$\unicode[STIX]{x1D702}(z)$.
So far we have discussed transformations of ![]() $\sum _{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}$ for
$\sum _{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}$ for ![]() $h\geqslant N/2$. Now let
$h\geqslant N/2$. Now let ![]() $h<N/2$. When
$h<N/2$. When ![]() $N$ is even, we are able to transform the series for any integer value of
$N$ is even, we are able to transform the series for any integer value of ![]() $h<N/2$. However, when
$h<N/2$. However, when ![]() $N$ is odd, we succeed in obtaining a transformation only for
$N$ is odd, we succeed in obtaining a transformation only for ![]() $0\leqslant h<N/2$ as the series consisting of
$0\leqslant h<N/2$ as the series consisting of ![]() $\sin (2\unicode[STIX]{x1D70B}na)$, logarithm and digamma functions in the summand does not converge for
$\sin (2\unicode[STIX]{x1D70B}na)$, logarithm and digamma functions in the summand does not converge for ![]() $h<0$.
$h<0$.
Theorem 2.10. Let ![]() $N$ be a positive integer and
$N$ be a positive integer and ![]() $h$ be a positive integer such that
$h$ be a positive integer such that ![]() $0\leqslant h<N/2$. Let
$0\leqslant h<N/2$. Let ![]() $x>0$ and
$x>0$ and ![]() $0<a\leqslant 1$.
$0<a\leqslant 1$.
(i) Let ![]() $N$ be odd and
$N$ be odd and ![]() $S(x,a)$ be defined as in (2.3). If
$S(x,a)$ be defined as in (2.3). If ![]() $g(N,h,a)$ is defined by
$g(N,h,a)$ is defined by
 $$\begin{eqnarray}g(N,h,a):=\left\{\begin{array}{@{}ll@{}}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D701}(-N+2h)\quad & \text{if }a=1,\\ 0\quad & \text{if }0<a<1\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g(N,h,a):=\left\{\begin{array}{@{}ll@{}}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D701}(-N+2h)\quad & \text{if }a=1,\\ 0\quad & \text{if }0<a<1\end{array}\right.\end{eqnarray}$$then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D701}(2h)}{x}+\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{N-2h+1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{N-2h+1}{N},a\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,x^{-\frac{(N-2h+1)}{N}}+S(x,a)+g(N,h,a).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D701}(2h)}{x}+\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{N-2h+1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{N-2h+1}{N},a\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,x^{-\frac{(N-2h+1)}{N}}+S(x,a)+g(N,h,a).\end{eqnarray}$$ (ii) If ![]() $N$ is even and
$N$ is even and ![]() $S(x,a)$ is defined as in (2.4), then
$S(x,a)$ is defined as in (2.4), then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D701}(2h)}{x}+\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{N-2h+1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{N-2h+1}{N},a\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,x^{-\frac{(N-2h+1)}{N}}+S(x,a).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D701}(2h)}{x}+\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{N-2h+1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{N-2h+1}{N},a\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,x^{-\frac{(N-2h+1)}{N}}+S(x,a).\end{eqnarray}$$ In addition, (2.17) holds also when ![]() $h<0$.
$h<0$.
Remark 5. The method described in Remark 2 for extending the formula in Theorem 2.1 to ![]() $a>1$ applies to the above theorem as well.
$a>1$ applies to the above theorem as well.
Remark 6. Note that the right-hand side of (2.17) is exactly the same as that of (2.1) since for ![]() $h<N/2$,
$h<N/2$, ![]() $N$ even, the term
$N$ even, the term ![]() $-(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$ as well as the two finite sums in
$-(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$ as well as the two finite sums in ![]() $P(x,a)$, as defined in (2.2), vanish.
$P(x,a)$, as defined in (2.2), vanish.
Kanemitsu et al. [Reference Kanemitsu, Tanigawa and Yoshimoto35] have obtained the above result for ![]() $a=1$.
$a=1$.
We now give a special case of part (i) of the above theorem.
Corollary 2.11. Let ![]() $0<a\leqslant 1$. Let
$0<a\leqslant 1$. Let ![]() $g(N,h,a)$ be defined in (2.15). If
$g(N,h,a)$ be defined in (2.15). If ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FD}$ are two positive numbers such that
$\unicode[STIX]{x1D6FD}$ are two positive numbers such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$, then
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}\mathop{\sum }_{n=1}^{\infty }\frac{ne^{2n\unicode[STIX]{x1D6FC}(1-a)}}{e^{2n\unicode[STIX]{x1D6FC}}-1}+\unicode[STIX]{x1D6FD}\mathop{\sum }_{n=1}^{\infty }\frac{n\cos (2\unicode[STIX]{x1D70B}na)}{e^{2n\unicode[STIX]{x1D6FD}}-1}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}g(1,0,a)+\frac{\unicode[STIX]{x1D713}^{\prime }(a)}{4\unicode[STIX]{x1D6FC}}-\frac{1}{4}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }n\sin (2\unicode[STIX]{x1D70B}na)\bigg\{\log \biggl(\frac{n\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{in\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-in\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)\biggr)\bigg\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}\mathop{\sum }_{n=1}^{\infty }\frac{ne^{2n\unicode[STIX]{x1D6FC}(1-a)}}{e^{2n\unicode[STIX]{x1D6FC}}-1}+\unicode[STIX]{x1D6FD}\mathop{\sum }_{n=1}^{\infty }\frac{n\cos (2\unicode[STIX]{x1D70B}na)}{e^{2n\unicode[STIX]{x1D6FD}}-1}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}g(1,0,a)+\frac{\unicode[STIX]{x1D713}^{\prime }(a)}{4\unicode[STIX]{x1D6FC}}-\frac{1}{4}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }n\sin (2\unicode[STIX]{x1D70B}na)\bigg\{\log \biggl(\frac{n\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{in\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-in\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)\biggr)\bigg\}.\end{eqnarray}$$ When ![]() $a=1$, (2.18) gives a result of Schlömilch [Reference Schlömilch58], rediscovered by Ramanujan [Reference Ramanujan55, Ch. 14, Section 8, Corollary (i)], [Reference Ramanujan56, page 318, formula (23)]:
$a=1$, (2.18) gives a result of Schlömilch [Reference Schlömilch58], rediscovered by Ramanujan [Reference Ramanujan55, Ch. 14, Section 8, Corollary (i)], [Reference Ramanujan56, page 318, formula (23)]:
Let ![]() $q=e^{2\unicode[STIX]{x1D70B}iz},z\in \mathbb{H}$. Then the analytic continuation of the above formula for
$q=e^{2\unicode[STIX]{x1D70B}iz},z\in \mathbb{H}$. Then the analytic continuation of the above formula for ![]() $\text{Re}(\unicode[STIX]{x1D6FC})>0$,
$\text{Re}(\unicode[STIX]{x1D6FC})>0$, ![]() $\text{Re}(\unicode[STIX]{x1D6FD})>0$ is equivalent to the transformation formula for the Eisenstein series
$\text{Re}(\unicode[STIX]{x1D6FD})>0$ is equivalent to the transformation formula for the Eisenstein series ![]() $E_{2}(z):=1-24\sum _{n=1}^{\infty }\frac{nq^{n}}{1-q^{n}}$, namely,
$E_{2}(z):=1-24\sum _{n=1}^{\infty }\frac{nq^{n}}{1-q^{n}}$, namely, ![]() $E_{2}(\frac{-1}{z})=z^{2}E_{2}(z)+\frac{6z}{\unicode[STIX]{x1D70B}i}$.
$E_{2}(\frac{-1}{z})=z^{2}E_{2}(z)+\frac{6z}{\unicode[STIX]{x1D70B}i}$.
A counterpart of Theorem 2.4, which is just a reformulation of Theorem 2.1 for ![]() $N$ even, is now given in terms of
$N$ even, is now given in terms of ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FD}$.
$\unicode[STIX]{x1D6FD}$.
Theorem 2.12. Let ![]() $N$ be an even positive integer and
$N$ be an even positive integer and ![]() $m$ be any integer. Let
$m$ be any integer. Let ![]() $0<a\leqslant 1$. For any
$0<a\leqslant 1$. For any ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ satisfying
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ satisfying ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-(\frac{2Nm-1}{N+1})}\biggl(\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(2Nm)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{j=1}^{m}\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2N(m-j))(2^{N}\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm}\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\exp (-(2n)^{N}\unicode[STIX]{x1D6FC})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FD}^{-(\frac{2Nm-1}{N+1})}\frac{2^{2Nm-1}}{N}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\unicode[STIX]{x1D70B}^{-(\frac{1-2Nm}{N})}\unicode[STIX]{x1D6E4}\biggl(\frac{1-2Nm}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{1-2Nm}{N},a\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(-1)^{\frac{N}{2}+m}}{2^{2m-1-\frac{1}{N}}}\mathop{\sum }_{j=0}^{\frac{N}{2}-1}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl[\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}}\text{Im}\biggl(\frac{e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}}{\exp ((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{j+\frac{N}{2}+1}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\text{Re}\biggl(\frac{e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}}{\exp ((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1}\biggr)\biggr]\bigg\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N}{2}+1}2^{2Nm-1}\mathop{\sum }_{j=0}^{m}\frac{B_{2j}(a)B_{(2m+1-2j)N}}{(2j)!((2m+1-2j)N)!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)-N}{N+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-(\frac{2Nm-1}{N+1})}\biggl(\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(2Nm)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{j=1}^{m}\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2N(m-j))(2^{N}\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm}\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\exp (-(2n)^{N}\unicode[STIX]{x1D6FC})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FD}^{-(\frac{2Nm-1}{N+1})}\frac{2^{2Nm-1}}{N}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\unicode[STIX]{x1D70B}^{-(\frac{1-2Nm}{N})}\unicode[STIX]{x1D6E4}\biggl(\frac{1-2Nm}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{1-2Nm}{N},a\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(-1)^{\frac{N}{2}+m}}{2^{2m-1-\frac{1}{N}}}\mathop{\sum }_{j=0}^{\frac{N}{2}-1}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl[\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}}\text{Im}\biggl(\frac{e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}}{\exp ((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{j+\frac{N}{2}+1}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\text{Re}\biggl(\frac{e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}}{\exp ((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1}\biggr)\biggr]\bigg\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N}{2}+1}2^{2Nm-1}\mathop{\sum }_{j=0}^{m}\frac{B_{2j}(a)B_{(2m+1-2j)N}}{(2j)!((2m+1-2j)N)!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)-N}{N+1}}.\end{eqnarray}$$ When ![]() $a=1$, we recover [Reference Dixit and Maji21, Theorem 1.10], which itself is a generalization of Wigert’s formula [Reference Wigert67, pages 8–9, Equation (5)], [Reference Dixit and Maji21, Equation (1.2)].
$a=1$, we recover [Reference Dixit and Maji21, Theorem 1.10], which itself is a generalization of Wigert’s formula [Reference Wigert67, pages 8–9, Equation (5)], [Reference Dixit and Maji21, Equation (1.2)].
The interesting result we now give is reminiscent of the corrected version of Klusch’s formula given by Kanemitsu, Tanigawa and Yoshimoto in [Reference Kanemitsu, Tanigawa and Yoshimoto37, Proposition 1.1] but is actually very different in nature from the latter.
Theorem 2.13. Let ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ be positive numbers such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ be positive numbers such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=4\unicode[STIX]{x1D70B}^{3}$. For
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=4\unicode[STIX]{x1D70B}^{3}$. For ![]() $0<a<1$, we have
$0<a<1$, we have
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\exp (-an^{2}\unicode[STIX]{x1D6FC})}{1-\exp (-n^{2}\unicode[STIX]{x1D6FC})} & = & \displaystyle \frac{1}{2}\biggl(a-\frac{1}{2}\biggr)+\frac{\unicode[STIX]{x1D70B}^{2}}{6\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2\sqrt{\unicode[STIX]{x1D6FC}}}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\biggl(\frac{\sinh (\sqrt{n\unicode[STIX]{x1D6FD}})-\sin (\sqrt{n\unicode[STIX]{x1D6FD}})}{\cosh (\sqrt{n\unicode[STIX]{x1D6FD}})-\cos (\sqrt{n\unicode[STIX]{x1D6FD}})}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\biggl(\frac{\sinh (\sqrt{n\unicode[STIX]{x1D6FD}})+\sin (\sqrt{n\unicode[STIX]{x1D6FD}})}{\cosh (\sqrt{n\unicode[STIX]{x1D6FD}})-\cos (\sqrt{n\unicode[STIX]{x1D6FD}})}\biggr)\bigg\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\exp (-an^{2}\unicode[STIX]{x1D6FC})}{1-\exp (-n^{2}\unicode[STIX]{x1D6FC})} & = & \displaystyle \frac{1}{2}\biggl(a-\frac{1}{2}\biggr)+\frac{\unicode[STIX]{x1D70B}^{2}}{6\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2\sqrt{\unicode[STIX]{x1D6FC}}}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\biggl(\frac{\sinh (\sqrt{n\unicode[STIX]{x1D6FD}})-\sin (\sqrt{n\unicode[STIX]{x1D6FD}})}{\cosh (\sqrt{n\unicode[STIX]{x1D6FD}})-\cos (\sqrt{n\unicode[STIX]{x1D6FD}})}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\biggl(\frac{\sinh (\sqrt{n\unicode[STIX]{x1D6FD}})+\sin (\sqrt{n\unicode[STIX]{x1D6FD}})}{\cosh (\sqrt{n\unicode[STIX]{x1D6FD}})-\cos (\sqrt{n\unicode[STIX]{x1D6FD}})}\biggr)\bigg\}.\end{eqnarray}$$ In particular, when ![]() $a=1/2$,
$a=1/2$,
Remark 7. There are very few results in the literature on transformations of infinite series involving trigonometric functions with ![]() $n^{2}$ in their arguments. We are aware of only the ones from Ramanujan’s Lost Notebook [Reference Ramanujan56, page 196] which were proved by Berndt, Chan and Tanigawa [Reference Berndt, Chan and Tanigawa10], and new results of similar type that they themselves obtain. However, to the best of our knowledge, there is not any transformation for infinite series involving hyperbolic functions having
$n^{2}$ in their arguments. We are aware of only the ones from Ramanujan’s Lost Notebook [Reference Ramanujan56, page 196] which were proved by Berndt, Chan and Tanigawa [Reference Berndt, Chan and Tanigawa10], and new results of similar type that they themselves obtain. However, to the best of our knowledge, there is not any transformation for infinite series involving hyperbolic functions having ![]() $n^{2}$ in their arguments in the literature. Our result (2.21) fills this gap.
$n^{2}$ in their arguments in the literature. Our result (2.21) fills this gap.
This paper is organized as follows. Section 3 is devoted to finding new properties of Raabe’s cosine transform ![]() $\mathfrak{R}(y,w)$ and to proving Theorem 2.2. In Section 4, we prove Theorem 2.1 and also obtain, as its special case, Theorem 2.1 of Kanemitsu et al. from [Reference Kanemitsu, Tanigawa and Yoshimoto37]. We derive Theorem 2.3 and its equivalent version, that is, Theorem 2.4 in Section 5. The special cases of the latter when
$\mathfrak{R}(y,w)$ and to proving Theorem 2.2. In Section 4, we prove Theorem 2.1 and also obtain, as its special case, Theorem 2.1 of Kanemitsu et al. from [Reference Kanemitsu, Tanigawa and Yoshimoto37]. We derive Theorem 2.3 and its equivalent version, that is, Theorem 2.4 in Section 5. The special cases of the latter when ![]() $a$ takes the values
$a$ takes the values ![]() $\frac{1}{2}$ and
$\frac{1}{2}$ and ![]() $\frac{1}{4}$ are given in Sections 5.1 and 5.2. Section 6 is devoted to proving Theorem 2.7 and Corollaries 2.8, 2.9 and 6.1 that result from it. Theorem 2.10 and Corollary 2.11 are proved in Section 7. We prove Theorem 2.12 and Theorem 2.13 in Section 8. Some applications of our transformations are given in Section 9. We end the paper with some concluding remarks in Section 10.
$\frac{1}{4}$ are given in Sections 5.1 and 5.2. Section 6 is devoted to proving Theorem 2.7 and Corollaries 2.8, 2.9 and 6.1 that result from it. Theorem 2.10 and Corollary 2.11 are proved in Section 7. We prove Theorem 2.12 and Theorem 2.13 in Section 8. Some applications of our transformations are given in Section 9. We end the paper with some concluding remarks in Section 10.
3 Some results on Raabe’s cosine transform
The left side of (2.6) is an infinite series whose summand is Raabe’s cosine transform defined in (2.5). In order to prove Theorem 2.2 one cannot interchange the order of summation and integration since that leads to a divergent integral. A version of the classical Poisson summation formula [Reference Titchmarsh64, pages 60–61] states that if ![]() $f(t)$ is continuous and of bounded variation on
$f(t)$ is continuous and of bounded variation on ![]() $[0,\infty )$, and if
$[0,\infty )$, and if ![]() $\int _{0}^{\infty }f(t)\,\text{d}t$ exists, then
$\int _{0}^{\infty }f(t)\,\text{d}t$ exists, then
The desired series of which we would like to obtain a closed form is the one on the right side of the above equation with ![]() $f(t)=\frac{4\unicode[STIX]{x1D70B}^{2}t}{4\unicode[STIX]{x1D70B}^{2}t^{2}+u^{2}}$, as can be easily seen by a simple change of variable. Unfortunately this formula is also inapplicable toward proving Theorem 2.2 because the hypothesis that
$f(t)=\frac{4\unicode[STIX]{x1D70B}^{2}t}{4\unicode[STIX]{x1D70B}^{2}t^{2}+u^{2}}$, as can be easily seen by a simple change of variable. Unfortunately this formula is also inapplicable toward proving Theorem 2.2 because the hypothesis that ![]() $\int _{0}^{\infty }f(t)\,\text{d}t$ be convergent is not satisfied. The idea is to use Guinand’s following generalization of Poisson’s summation formula.
$\int _{0}^{\infty }f(t)\,\text{d}t$ be convergent is not satisfied. The idea is to use Guinand’s following generalization of Poisson’s summation formula.
Theorem 3.1. If ![]() $f(x)$ is an integral,
$f(x)$ is an integral, ![]() $f(x)$ tends to zero as
$f(x)$ tends to zero as ![]() $x\rightarrow \infty$, and
$x\rightarrow \infty$, and ![]() $xf^{\prime }(x)$ belongs to
$xf^{\prime }(x)$ belongs to ![]() $L^{p}(0,\infty )$, for some p,
$L^{p}(0,\infty )$, for some p, ![]() $1<p\leqslant 2$, then
$1<p\leqslant 2$, then
where
However, before using Theorem 3.1, it is imperative to obtain some results on Raabe’s cosine transform. We begin with the following identity which readily depicts the asymptotic behavior of Raabe’s cosine transform for positive small values of ![]() $y$.
$y$.
Lemma 3.2. For ![]() $y>0$ and
$y>0$ and ![]() $\text{Re}(w)>0$, the following identity holds:
$\text{Re}(w)>0$, the following identity holds:
In particular, as ![]() $y\rightarrow 0^{+}$,
$y\rightarrow 0^{+}$,
Proof. First let ![]() $w>0$. From [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 428, Formula 3.723.5],
$w>0$. From [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 428, Formula 3.723.5],
where ![]() $\text{Ei}(x)$ is the exponential integral defined for
$\text{Ei}(x)$ is the exponential integral defined for ![]() $x>0$ by [Reference Jahnke and Emde34, page 1]
$x>0$ by [Reference Jahnke and Emde34, page 1] ![]() $\text{Ei}(-x)=-\int _{x}^{\infty }e^{-t}/t\,\text{d}t$. Thus the exponential integral function is related to logarithmic integral
$\text{Ei}(-x)=-\int _{x}^{\infty }e^{-t}/t\,\text{d}t$. Thus the exponential integral function is related to logarithmic integral ![]() $\text{li}(x)=\int _{0}^{x}\frac{\text{d}t}{\log (t)}$ by
$\text{li}(x)=\int _{0}^{x}\frac{\text{d}t}{\log (t)}$ by
Also [Reference Jahnke and Emde34, page 3],
Thus from (3.3)–(3.5), we see that
Now Dixon and Ferrar [Reference Dixon and Ferrar23, page 165, Equation (5.4)] have proved that
where [Reference Dixon and Ferrar22, Equation (3.12)]
Let ![]() $\unicode[STIX]{x1D708}=1/2$ in (3.8), use the duplication formula for the gamma function and then combine the resulting identity with (3.6) and (3.7) to obtain (3.1) for
$\unicode[STIX]{x1D708}=1/2$ in (3.8), use the duplication formula for the gamma function and then combine the resulting identity with (3.6) and (3.7) to obtain (3.1) for ![]() $w>0$. Since both sides of (3.1) are analytic for
$w>0$. Since both sides of (3.1) are analytic for ![]() $\text{Re}(w)>0$, we obtain (3.1) in this region by analytic continuation. To prove (3.2), divide both sides of (3.1) by the first term of the right-hand side and note that
$\text{Re}(w)>0$, we obtain (3.1) in this region by analytic continuation. To prove (3.2), divide both sides of (3.1) by the first term of the right-hand side and note that ![]() $\unicode[STIX]{x1D713}(1)=-\unicode[STIX]{x1D6FE}$ as well as
$\unicode[STIX]{x1D713}(1)=-\unicode[STIX]{x1D6FE}$ as well as ![]() $\lim _{y\rightarrow 0^{+}}(wy)^{2k}(\unicode[STIX]{x1D713}(2k+1)-\log (wy))/((2k)!(-\unicode[STIX]{x1D6FE}-\log (wy)))=0$ for
$\lim _{y\rightarrow 0^{+}}(wy)^{2k}(\unicode[STIX]{x1D713}(2k+1)-\log (wy))/((2k)!(-\unicode[STIX]{x1D6FE}-\log (wy)))=0$ for ![]() $k\geqslant 1$.◻
$k\geqslant 1$.◻
Second proof. For ![]() $0<\text{Re}(s)<1+2\text{Re}(\unicode[STIX]{x1D708})$ [Reference Oberhettinger49, page 43, Formula (5.10)],
$0<\text{Re}(s)<1+2\text{Re}(\unicode[STIX]{x1D708})$ [Reference Oberhettinger49, page 43, Formula (5.10)],
 $$\begin{eqnarray}\displaystyle \int _{0}^{\infty }\frac{\cos (yt)}{(w^{2}+t^{2})^{\unicode[STIX]{x1D708}}}t^{s-1}\text{d}t & = & \displaystyle \frac{w^{s-2\unicode[STIX]{x1D708}}}{2}B\biggl(\frac{s}{2},\unicode[STIX]{x1D708}-\frac{s}{2}\biggr)_{1}F_{2}\biggl(\frac{s}{2};1-\unicode[STIX]{x1D708}+\frac{s}{2},\frac{1}{2};\frac{w^{2}y^{2}}{4}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2}\biggl(\frac{y}{2}\biggr)^{2\unicode[STIX]{x1D708}-s}\frac{\unicode[STIX]{x1D6E4}(\frac{s}{2}-\unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}(\frac{1}{2}+\unicode[STIX]{x1D708}-\frac{s}{2})}\nonumber\\ \displaystyle & & \displaystyle \times \,_{1}F_{2}\biggl(\unicode[STIX]{x1D708};\frac{1}{2}+\unicode[STIX]{x1D708}-\frac{s}{2},1+\unicode[STIX]{x1D708}-\frac{s}{2};\frac{w^{2}y^{2}}{4}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{\infty }\frac{\cos (yt)}{(w^{2}+t^{2})^{\unicode[STIX]{x1D708}}}t^{s-1}\text{d}t & = & \displaystyle \frac{w^{s-2\unicode[STIX]{x1D708}}}{2}B\biggl(\frac{s}{2},\unicode[STIX]{x1D708}-\frac{s}{2}\biggr)_{1}F_{2}\biggl(\frac{s}{2};1-\unicode[STIX]{x1D708}+\frac{s}{2},\frac{1}{2};\frac{w^{2}y^{2}}{4}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2}\biggl(\frac{y}{2}\biggr)^{2\unicode[STIX]{x1D708}-s}\frac{\unicode[STIX]{x1D6E4}(\frac{s}{2}-\unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}(\frac{1}{2}+\unicode[STIX]{x1D708}-\frac{s}{2})}\nonumber\\ \displaystyle & & \displaystyle \times \,_{1}F_{2}\biggl(\unicode[STIX]{x1D708};\frac{1}{2}+\unicode[STIX]{x1D708}-\frac{s}{2},1+\unicode[STIX]{x1D708}-\frac{s}{2};\frac{w^{2}y^{2}}{4}\biggr),\nonumber\end{eqnarray}$$ where ![]() $B(z_{1},z_{2}):=\frac{\unicode[STIX]{x1D6E4}(z_{1})\unicode[STIX]{x1D6E4}(z_{2})}{\unicode[STIX]{x1D6E4}(z_{1}+z_{2})}$ is the beta function. Let
$B(z_{1},z_{2}):=\frac{\unicode[STIX]{x1D6E4}(z_{1})\unicode[STIX]{x1D6E4}(z_{2})}{\unicode[STIX]{x1D6E4}(z_{1}+z_{2})}$ is the beta function. Let ![]() $\unicode[STIX]{x1D708}=1$, so for
$\unicode[STIX]{x1D708}=1$, so for ![]() $0<\text{Re}(s)<3$, we haveFootnote 2
$0<\text{Re}(s)<3$, we haveFootnote 2
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }\frac{\cos (yt)}{w^{2}+t^{2}}t^{s-1}\text{d}t\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2}\biggl(\frac{y}{2}\biggr)^{2-s}\frac{\unicode[STIX]{x1D6E4}(\frac{s}{2}-1)}{\unicode[STIX]{x1D6E4}(\frac{3}{2}-\frac{s}{2})}\;_{1}F_{2}\biggl(1;\frac{3}{2}-\frac{s}{2},2-\frac{s}{2};\frac{w^{2}y^{2}}{4}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\unicode[STIX]{x1D70B}w^{s-2}\text{cosec}\biggl(\frac{\unicode[STIX]{x1D70B}s}{2}\biggr)\cosh (wy).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }\frac{\cos (yt)}{w^{2}+t^{2}}t^{s-1}\text{d}t\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2}\biggl(\frac{y}{2}\biggr)^{2-s}\frac{\unicode[STIX]{x1D6E4}(\frac{s}{2}-1)}{\unicode[STIX]{x1D6E4}(\frac{3}{2}-\frac{s}{2})}\;_{1}F_{2}\biggl(1;\frac{3}{2}-\frac{s}{2},2-\frac{s}{2};\frac{w^{2}y^{2}}{4}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\unicode[STIX]{x1D70B}w^{s-2}\text{cosec}\biggl(\frac{\unicode[STIX]{x1D70B}s}{2}\biggr)\cosh (wy).\end{eqnarray}$$ Note that the following expansions are valid as ![]() $z\rightarrow 0$:
$z\rightarrow 0$:
where ![]() $(a)_{n}:=a(a+1)\cdots (a+n-1)$ is the Pochhammer symbol. Now (3.12) implies
$(a)_{n}:=a(a+1)\cdots (a+n-1)$ is the Pochhammer symbol. Now (3.12) implies
as ![]() $z\rightarrow 0$. Since
$z\rightarrow 0$. Since ![]() $_{1}F_{2}(1;\frac{1}{2}-z,1-z;\frac{w^{2}y^{2}}{4})=\sum _{k=0}^{\infty }\frac{1}{(1-2z)_{2k}}(wy)^{2k}$ is uniformly convergent on
$_{1}F_{2}(1;\frac{1}{2}-z,1-z;\frac{w^{2}y^{2}}{4})=\sum _{k=0}^{\infty }\frac{1}{(1-2z)_{2k}}(wy)^{2k}$ is uniformly convergent on ![]() $|z|\leqslant r_{1}<1$, employing (3.13) leads to
$|z|\leqslant r_{1}<1$, employing (3.13) leads to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{0.0pt}_{1}F_{2}\biggl(1;\frac{1}{2}-z,1-z;\frac{w^{2}y^{2}}{4}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=0}^{\infty }\frac{(wy)^{2k}}{(2k)!}(1+2z(\unicode[STIX]{x1D713}(2k+1)-\unicode[STIX]{x1D713}(1))+O(z^{2})).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{0.0pt}_{1}F_{2}\biggl(1;\frac{1}{2}-z,1-z;\frac{w^{2}y^{2}}{4}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=0}^{\infty }\frac{(wy)^{2k}}{(2k)!}(1+2z(\unicode[STIX]{x1D713}(2k+1)-\unicode[STIX]{x1D713}(1))+O(z^{2})).\end{eqnarray}$$ Letting ![]() $s=2z+2$ in (3.9) with
$s=2z+2$ in (3.9) with ![]() $z\rightarrow 0$, and then invoking (3.10), (3.11) and (3.14), we get
$z\rightarrow 0$, and then invoking (3.10), (3.11) and (3.14), we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }\frac{t\cos (yt)}{w^{2}+t^{2}}\,\text{d}t\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{z\rightarrow 0}\bigg\{e^{-2z\log (y)}\unicode[STIX]{x1D6E4}(2z)\cos (\unicode[STIX]{x1D70B}z)\;_{1}F_{2}\biggl(1;\frac{1}{2}-z,1-z;\frac{w^{2}y^{2}}{4}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\unicode[STIX]{x1D70B}}{2}e^{2z\log (w)}\text{cosec}(\unicode[STIX]{x1D70B}z)\cosh (wy)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{z\rightarrow 0}\biggl[(1-2z\log (y)+2z^{2}\log ^{2}(y)+\cdots )\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\frac{1}{2z}-\unicode[STIX]{x1D6FE}+\biggl(\unicode[STIX]{x1D6FE}^{2}+\frac{\unicode[STIX]{x1D70B}^{2}}{6}\biggr)z+\cdots \biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(1-\frac{(\unicode[STIX]{x1D70B}z)^{2}}{2!}+\cdots \biggr)\biggl(\mathop{\sum }_{k=0}^{\infty }\frac{(wy)^{2k}}{(2k)!}(1+2z(\unicode[STIX]{x1D713}(2k+1)-\unicode[STIX]{x1D713}(1))+\cdots )\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\biggl(\frac{1}{2z}+\log (w)+\biggl(\frac{\unicode[STIX]{x1D70B}^{2}}{12}+\log ^{2}(w)\biggr)z+\cdots \biggr)\cosh (wy)\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=0}^{\infty }\frac{(wy)^{2k}}{(2k)!}(\unicode[STIX]{x1D713}(2k+1)-\log (wy)).\hspace{128.00021pt}\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }\frac{t\cos (yt)}{w^{2}+t^{2}}\,\text{d}t\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{z\rightarrow 0}\bigg\{e^{-2z\log (y)}\unicode[STIX]{x1D6E4}(2z)\cos (\unicode[STIX]{x1D70B}z)\;_{1}F_{2}\biggl(1;\frac{1}{2}-z,1-z;\frac{w^{2}y^{2}}{4}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\unicode[STIX]{x1D70B}}{2}e^{2z\log (w)}\text{cosec}(\unicode[STIX]{x1D70B}z)\cosh (wy)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{z\rightarrow 0}\biggl[(1-2z\log (y)+2z^{2}\log ^{2}(y)+\cdots )\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\frac{1}{2z}-\unicode[STIX]{x1D6FE}+\biggl(\unicode[STIX]{x1D6FE}^{2}+\frac{\unicode[STIX]{x1D70B}^{2}}{6}\biggr)z+\cdots \biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(1-\frac{(\unicode[STIX]{x1D70B}z)^{2}}{2!}+\cdots \biggr)\biggl(\mathop{\sum }_{k=0}^{\infty }\frac{(wy)^{2k}}{(2k)!}(1+2z(\unicode[STIX]{x1D713}(2k+1)-\unicode[STIX]{x1D713}(1))+\cdots )\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\biggl(\frac{1}{2z}+\log (w)+\biggl(\frac{\unicode[STIX]{x1D70B}^{2}}{12}+\log ^{2}(w)\biggr)z+\cdots \biggr)\cosh (wy)\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=0}^{\infty }\frac{(wy)^{2k}}{(2k)!}(\unicode[STIX]{x1D713}(2k+1)-\log (wy)).\hspace{128.00021pt}\square\nonumber\end{eqnarray}$$ Next, the asymptotic expansion of Raabe’s cosine transform for large values of ![]() $y$ is obtained.
$y$ is obtained.
Lemma 3.3. Let ![]() $\text{Re}(w)>0$. As
$\text{Re}(w)>0$. As ![]() $y\rightarrow \infty$,
$y\rightarrow \infty$,
Proof. Here, we use the analogue of Watson’s lemma for Laplace transform in the setting of Fourier transforms [Reference Olver50], [Reference Dai and Naylor17, Equations (1.3), (1.4)]. It says that if the form of ![]() $h(t)$ near
$h(t)$ near ![]() $t=0$ is given as a series of algebraic powers, that is,
$t=0$ is given as a series of algebraic powers, that is,
as ![]() $t\rightarrow 0^{+}$, then under certain restrictions on
$t\rightarrow 0^{+}$, then under certain restrictions on ![]() $h$ (see [Reference Olver50], [Reference Dai and Naylor17, Section 2] for the same),
$h$ (see [Reference Olver50], [Reference Dai and Naylor17, Section 2] for the same),
as ![]() $s\rightarrow \infty$. Let
$s\rightarrow \infty$. Let ![]() $h(t)=t/(t^{2}+w^{2})$. Then it is easy to see that
$h(t)=t/(t^{2}+w^{2})$. Then it is easy to see that ![]() $h(t)$ satisfies (3.16) with
$h(t)$ satisfies (3.16) with ![]() $\unicode[STIX]{x1D706}=1$ and
$\unicode[STIX]{x1D706}=1$ and
Now invoking (3.17) twice, once with ![]() $s=y$ and then with
$s=y$ and then with ![]() $s=-y$, and then adding the resulting two identities, we arrive at
$s=-y$, and then adding the resulting two identities, we arrive at
 $$\begin{eqnarray}\displaystyle \mathfrak{R}(y,w) & {\sim} & \displaystyle \frac{1}{2}\mathop{\sum }_{n=0}^{\infty }b_{n}e^{i(n+1)\unicode[STIX]{x1D70B}/2}\unicode[STIX]{x1D6E4}(n+1)y^{-n-1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\mathop{\sum }_{n=0}^{\infty }b_{n}e^{i(n+1)\unicode[STIX]{x1D70B}/2}\unicode[STIX]{x1D6E4}(n+1)(-y)^{-n-1}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{b_{2n-1}(2n-1)!\cos (n\unicode[STIX]{x1D70B})}{y^{2n}}=-\mathop{\sum }_{n=1}^{\infty }\frac{(2n-1)!}{w^{2n}y^{2n}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{R}(y,w) & {\sim} & \displaystyle \frac{1}{2}\mathop{\sum }_{n=0}^{\infty }b_{n}e^{i(n+1)\unicode[STIX]{x1D70B}/2}\unicode[STIX]{x1D6E4}(n+1)y^{-n-1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\mathop{\sum }_{n=0}^{\infty }b_{n}e^{i(n+1)\unicode[STIX]{x1D70B}/2}\unicode[STIX]{x1D6E4}(n+1)(-y)^{-n-1}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{b_{2n-1}(2n-1)!\cos (n\unicode[STIX]{x1D70B})}{y^{2n}}=-\mathop{\sum }_{n=1}^{\infty }\frac{(2n-1)!}{w^{2n}y^{2n}}.\nonumber\end{eqnarray}$$This completes the proof. ◻
We now give two proofs of a crucial lemma which is interesting in itself, and which is employed in the proof of Theorem 2.2. Each has its advantage over the other in that one is instructive and the other employs known identities on special functions. We begin with the instructive one first.
Lemma 3.4. For ![]() $y>0$ and
$y>0$ and ![]() $\text{Re}(u)>0$,
$\text{Re}(u)>0$,
Proof. It is important to note that the above double integral does not converge absolutely and hence Fubini’s theorem is inapplicable, that is, we cannot change the order of integration. First assume ![]() $u>0$. We prove (3.18) in the form
$u>0$. We prove (3.18) in the form ![]() $\int _{0}^{\infty }\mathfrak{R}(y,w)\,\text{d}y=0$, where
$\int _{0}^{\infty }\mathfrak{R}(y,w)\,\text{d}y=0$, where ![]() $w=2\unicode[STIX]{x1D70B}u$ and
$w=2\unicode[STIX]{x1D70B}u$ and ![]() $\mathfrak{R}(y,w)$ is defined in (2.5). First of all, (3.2) and (3.15) imply that this integral exists. Now let
$\mathfrak{R}(y,w)$ is defined in (2.5). First of all, (3.2) and (3.15) imply that this integral exists. Now let ![]() $N$ be a positive integer and consider the integral
$N$ be a positive integer and consider the integral
With the help of Fubini’s theorem, one can write
 $$\begin{eqnarray}\displaystyle I(w,N) & = & \displaystyle \int _{0}^{\infty }\frac{t}{w^{2}+t^{2}}\,\text{d}t\int _{0}^{\infty }e^{-\frac{y}{N}}\cos (yt)\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{N}\int _{0}^{\infty }\frac{t}{(w^{2}+t^{2})(\frac{1}{N^{2}}+t^{2})}\,\text{d}t\nonumber\\ \displaystyle & = & \displaystyle \frac{N}{1-N^{2}w^{2}}\int _{0}^{\infty }\biggl(\frac{t}{w^{2}+t^{2}}-\frac{t}{\frac{1}{N^{2}}+t^{2}}\biggr)\,\text{d}t\nonumber\\ \displaystyle & = & \displaystyle \frac{N}{2(1-N^{2}w^{2})}\lim _{A\rightarrow \infty }\bigg\{[\log (w^{2}+t^{2})]_{0}^{A}-\biggl[\log \biggl(\frac{1}{N^{2}}+t^{2}\biggr)\biggr]_{0}^{A}\bigg\}\nonumber\\ \displaystyle & = & \displaystyle \frac{N}{2(1-N^{2}w^{2})}\lim _{A\rightarrow \infty }\bigg\{\log \biggl(\frac{w^{2}+A^{2}}{\frac{1}{N^{2}}+A^{2}}\biggr)+2\log \biggl(\frac{1}{Nw}\biggr)\bigg\}\nonumber\\ \displaystyle & = & \displaystyle \frac{N\log (Nw)}{N^{2}w^{2}-1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(w,N) & = & \displaystyle \int _{0}^{\infty }\frac{t}{w^{2}+t^{2}}\,\text{d}t\int _{0}^{\infty }e^{-\frac{y}{N}}\cos (yt)\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{N}\int _{0}^{\infty }\frac{t}{(w^{2}+t^{2})(\frac{1}{N^{2}}+t^{2})}\,\text{d}t\nonumber\\ \displaystyle & = & \displaystyle \frac{N}{1-N^{2}w^{2}}\int _{0}^{\infty }\biggl(\frac{t}{w^{2}+t^{2}}-\frac{t}{\frac{1}{N^{2}}+t^{2}}\biggr)\,\text{d}t\nonumber\\ \displaystyle & = & \displaystyle \frac{N}{2(1-N^{2}w^{2})}\lim _{A\rightarrow \infty }\bigg\{[\log (w^{2}+t^{2})]_{0}^{A}-\biggl[\log \biggl(\frac{1}{N^{2}}+t^{2}\biggr)\biggr]_{0}^{A}\bigg\}\nonumber\\ \displaystyle & = & \displaystyle \frac{N}{2(1-N^{2}w^{2})}\lim _{A\rightarrow \infty }\bigg\{\log \biggl(\frac{w^{2}+A^{2}}{\frac{1}{N^{2}}+A^{2}}\biggr)+2\log \biggl(\frac{1}{Nw}\biggr)\bigg\}\nonumber\\ \displaystyle & = & \displaystyle \frac{N\log (Nw)}{N^{2}w^{2}-1},\end{eqnarray}$$ since ![]() $\lim _{A\rightarrow \infty }\log (\frac{w^{2}+A^{2}}{\frac{1}{N^{2}}+A^{2}})=0$. Now note that
$\lim _{A\rightarrow \infty }\log (\frac{w^{2}+A^{2}}{\frac{1}{N^{2}}+A^{2}})=0$. Now note that ![]() $e^{-\frac{y}{N}}\mathfrak{R}(y,w)\rightarrow \mathfrak{R}(y,w)$ pointwise as
$e^{-\frac{y}{N}}\mathfrak{R}(y,w)\rightarrow \mathfrak{R}(y,w)$ pointwise as ![]() $N\rightarrow \infty$ and
$N\rightarrow \infty$ and ![]() $|e^{-\frac{y}{N}}\mathfrak{R}(y,w)|\leqslant \mathfrak{R}(y,w)$. Also, as mentioned before, the fact that
$|e^{-\frac{y}{N}}\mathfrak{R}(y,w)|\leqslant \mathfrak{R}(y,w)$. Also, as mentioned before, the fact that ![]() $\mathfrak{R}(y,w)$ is integrable, as a function of
$\mathfrak{R}(y,w)$ is integrable, as a function of ![]() $y$ from
$y$ from ![]() $0$ to
$0$ to ![]() $\infty$, is clear from (3.2) and (3.15). Hence letting
$\infty$, is clear from (3.2) and (3.15). Hence letting ![]() $N\rightarrow \infty$ on both sides of (3.19) and employing Lebesgue’s dominated convergence theorem, we see that
$N\rightarrow \infty$ on both sides of (3.19) and employing Lebesgue’s dominated convergence theorem, we see that
 $$\begin{eqnarray}\displaystyle \lim _{N\rightarrow \infty }I(w,N) & = & \displaystyle \int _{0}^{\infty }\lim _{N\rightarrow \infty }e^{-\frac{y}{N}}\mathfrak{R}(y,w)\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\mathfrak{R}(y,w)\,\text{d}y,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{N\rightarrow \infty }I(w,N) & = & \displaystyle \int _{0}^{\infty }\lim _{N\rightarrow \infty }e^{-\frac{y}{N}}\mathfrak{R}(y,w)\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\mathfrak{R}(y,w)\,\text{d}y,\nonumber\end{eqnarray}$$ whereas (3.20) implies that ![]() $\lim _{N\rightarrow \infty }I(w,N)=0$. Together, these complete the proof of (3.18) for
$\lim _{N\rightarrow \infty }I(w,N)=0$. Together, these complete the proof of (3.18) for ![]() $u>0$. Note that the left-hand side of (3.18) is analytic for
$u>0$. Note that the left-hand side of (3.18) is analytic for ![]() $\text{Re}(u)>0$ as can be seen using [Reference Temme61, Theorem 2.3, page 30]. Hence by analytic continuation, the result holds for
$\text{Re}(u)>0$ as can be seen using [Reference Temme61, Theorem 2.3, page 30]. Hence by analytic continuation, the result holds for ![]() $\text{Re}(u)>0$.◻
$\text{Re}(u)>0$.◻
Second proof of (3.18). By Slater’s theorem [Reference Olver, Lozier, Boisvert and Clark51, page 415, Equation 16.17.2], if ![]() $p\leqslant q$ and
$p\leqslant q$ and ![]() $b_{j}-b_{k}\not \in \mathbb{Z}$ for
$b_{j}-b_{k}\not \in \mathbb{Z}$ for ![]() $j\neq k,1\leqslant j,k\leqslant n$, then
$j\neq k,1\leqslant j,k\leqslant n$, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle G_{p,q}^{m,n}\left(z\biggm\vert\begin{array}{@{}c@{}}a_{1},\ldots ,a_{p}\\ b_{1},\ldots ,b_{q}\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=1}^{m}A_{p,q,k}^{m,n}(z)_{p}F_{q-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left((-1)^{p-m-n}z\biggm\vert\begin{array}{@{}c@{}}1+b_{k}-a_{1},\ldots ,1+b_{k}-a_{p}\\ 1+b_{k}-b_{1},\cdots \ast \cdots \,,1+b_{k}-b_{q}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle G_{p,q}^{m,n}\left(z\biggm\vert\begin{array}{@{}c@{}}a_{1},\ldots ,a_{p}\\ b_{1},\ldots ,b_{q}\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=1}^{m}A_{p,q,k}^{m,n}(z)_{p}F_{q-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left((-1)^{p-m-n}z\biggm\vert\begin{array}{@{}c@{}}1+b_{k}-a_{1},\ldots ,1+b_{k}-a_{p}\\ 1+b_{k}-b_{1},\cdots \ast \cdots \,,1+b_{k}-b_{q}\end{array}\right),\end{eqnarray}$$ where ![]() $\ast$ indicates that the entry
$\ast$ indicates that the entry ![]() $1+b_{k}-b_{k}$ is omitted and
$1+b_{k}-b_{k}$ is omitted and
Here, ![]() $G_{p,q}^{\,m,n}\big(z\big|\begin{smallmatrix}a_{1},\ldots ,a_{p}\\ b_{1},\ldots ,b_{q}\end{smallmatrix}\!\big)$ is the Meijer
$G_{p,q}^{\,m,n}\big(z\big|\begin{smallmatrix}a_{1},\ldots ,a_{p}\\ b_{1},\ldots ,b_{q}\end{smallmatrix}\!\big)$ is the Meijer ![]() $G$-function [Reference Olver, Lozier, Boisvert and Clark51, page 415] and
$G$-function [Reference Olver, Lozier, Boisvert and Clark51, page 415] and ![]() $_{p}F_{q-1}$ is the generalized hypergeometric function.
$_{p}F_{q-1}$ is the generalized hypergeometric function.
Let ![]() $y>0$ and, as before,
$y>0$ and, as before, ![]() $w=2\unicode[STIX]{x1D70B}u$, where
$w=2\unicode[STIX]{x1D70B}u$, where ![]() $u\in \mathbb{C}$ with
$u\in \mathbb{C}$ with ![]() $\text{Re}(u)>0$. Now let
$\text{Re}(u)>0$. Now let ![]() $m=2,n=1,p=1,q=3,a_{1}=b_{2}=1-\frac{s}{2},b_{1}=0,b_{3}=1/2,z=w^{2}y^{2}/4$ in (3.21) and use the resulting identity along with (3.9) to obtain, for
$m=2,n=1,p=1,q=3,a_{1}=b_{2}=1-\frac{s}{2},b_{1}=0,b_{3}=1/2,z=w^{2}y^{2}/4$ in (3.21) and use the resulting identity along with (3.9) to obtain, for ![]() $0<\text{Re}(s)<3$,
$0<\text{Re}(s)<3$,
 $$\begin{eqnarray}\int _{0}^{\infty }\frac{\cos (yt)}{w^{2}+t^{2}}t^{s-1}\,\text{d}t=\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2}w^{s-2}G_{1,3}^{2,1}\left(\frac{w^{2}y^{2}}{4}\left|\begin{array}{@{}c@{}}\displaystyle 1-\frac{s}{2}\\ \displaystyle 0,1-\frac{s}{2},\frac{1}{2}\end{array}\right.\right).\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{\infty }\frac{\cos (yt)}{w^{2}+t^{2}}t^{s-1}\,\text{d}t=\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2}w^{s-2}G_{1,3}^{2,1}\left(\frac{w^{2}y^{2}}{4}\left|\begin{array}{@{}c@{}}\displaystyle 1-\frac{s}{2}\\ \displaystyle 0,1-\frac{s}{2},\frac{1}{2}\end{array}\right.\right).\end{eqnarray}$$ Substitute ![]() $s=2$ in the above equation and use the resulting identity to see that
$s=2$ in the above equation and use the resulting identity to see that
 $$\begin{eqnarray}\displaystyle \int _{0}^{\infty }\int _{0}^{\infty }\frac{t\cos (yt)}{w^{2}+t^{2}}\,\text{d}t\,\text{d}y & = & \displaystyle \int _{0}^{\infty }\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2}G_{1,3}^{2,1}\left(\frac{w^{2}y^{2}}{4}\biggm\vert\begin{array}{@{}c@{}}0\\ 0,0,\frac{1}{2}\end{array}\right)\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \frac{\sqrt{\unicode[STIX]{x1D70B}}}{4}\int _{0}^{\infty }G_{1,3}^{2,1}\left(\frac{w^{2}Y}{4}\biggm\vert\begin{array}{@{}c@{}}0\\ 0,0,\frac{1}{2}\end{array}\right)\frac{1}{\sqrt{Y}}\,\text{d}Y.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{\infty }\int _{0}^{\infty }\frac{t\cos (yt)}{w^{2}+t^{2}}\,\text{d}t\,\text{d}y & = & \displaystyle \int _{0}^{\infty }\frac{\sqrt{\unicode[STIX]{x1D70B}}}{2}G_{1,3}^{2,1}\left(\frac{w^{2}y^{2}}{4}\biggm\vert\begin{array}{@{}c@{}}0\\ 0,0,\frac{1}{2}\end{array}\right)\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \frac{\sqrt{\unicode[STIX]{x1D70B}}}{4}\int _{0}^{\infty }G_{1,3}^{2,1}\left(\frac{w^{2}Y}{4}\biggm\vert\begin{array}{@{}c@{}}0\\ 0,0,\frac{1}{2}\end{array}\right)\frac{1}{\sqrt{Y}}\,\text{d}Y.\end{eqnarray}$$From [Reference Prudnikov, Brychkov and Marichev53, page 293, Formula 2.24.2.1], for
 $$\begin{eqnarray}\displaystyle & \displaystyle m^{2}+n^{2}\neq 0,\quad c^{\ast }:=m+n-(p+q)/2>0,\quad |\text{arg}\,\unicode[STIX]{x1D702}|<c^{\ast }\unicode[STIX]{x1D70B},\unicode[STIX]{x1D702}\neq 0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle -\min _{1\leqslant j\leqslant m}\,\text{Re}(b_{j})<\text{Re}(s)<1-\max _{1\leqslant j\leqslant n}\,\text{Re}(a_{j}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle m^{2}+n^{2}\neq 0,\quad c^{\ast }:=m+n-(p+q)/2>0,\quad |\text{arg}\,\unicode[STIX]{x1D702}|<c^{\ast }\unicode[STIX]{x1D70B},\unicode[STIX]{x1D702}\neq 0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle -\min _{1\leqslant j\leqslant m}\,\text{Re}(b_{j})<\text{Re}(s)<1-\max _{1\leqslant j\leqslant n}\,\text{Re}(a_{j}), & \displaystyle \nonumber\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }G_{p,q}^{m,n}\left(\unicode[STIX]{x1D702}x\biggm\vert\begin{array}{@{}c@{}}a_{1},\ldots ,a_{p}\\ b_{1},\ldots ,b_{q}\end{array}\right)x^{s-1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D702}^{-s}\mathop{\prod }_{j=1}^{m}\unicode[STIX]{x1D6E4}(b_{j}+s)\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E4}(1-a_{j}-s)}{\mathop{\prod }_{j=m+1}^{q}\unicode[STIX]{x1D6E4}(1-b_{j}-s)\mathop{\prod }_{j=n+1}^{p}\unicode[STIX]{x1D6E4}(a_{j}+s)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }G_{p,q}^{m,n}\left(\unicode[STIX]{x1D702}x\biggm\vert\begin{array}{@{}c@{}}a_{1},\ldots ,a_{p}\\ b_{1},\ldots ,b_{q}\end{array}\right)x^{s-1}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D702}^{-s}\mathop{\prod }_{j=1}^{m}\unicode[STIX]{x1D6E4}(b_{j}+s)\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E4}(1-a_{j}-s)}{\mathop{\prod }_{j=m+1}^{q}\unicode[STIX]{x1D6E4}(1-b_{j}-s)\mathop{\prod }_{j=n+1}^{p}\unicode[STIX]{x1D6E4}(a_{j}+s)}.\nonumber\end{eqnarray}$$ Let ![]() $m=2,n=1,p=1,q=3$ and
$m=2,n=1,p=1,q=3$ and ![]() $a_{1}=b_{1}=b_{2}=0,b_{3}=\frac{1}{2}$,
$a_{1}=b_{1}=b_{2}=0,b_{3}=\frac{1}{2}$, ![]() $\unicode[STIX]{x1D702}=\frac{w^{2}}{4}$ and
$\unicode[STIX]{x1D702}=\frac{w^{2}}{4}$ and ![]() $x=Y$ in the above formula so that for
$x=Y$ in the above formula so that for ![]() $0<\text{Re}(s)<1$,
$0<\text{Re}(s)<1$,
Now let ![]() $s=1/2$ in the above equation and substitute the resultant in (3.23) to arrive at (3.18) since the Gamma function in the denominator on the right side has a pole at
$s=1/2$ in the above equation and substitute the resultant in (3.23) to arrive at (3.18) since the Gamma function in the denominator on the right side has a pole at ![]() $s=1/2$, whereas the ones in the numerator are well-defined. This completes the proof.◻
$s=1/2$, whereas the ones in the numerator are well-defined. This completes the proof.◻
Proof of Theorem 2.2.
Let
That the above integral exists is clear from the fact that ![]() $f(v)=\frac{v}{2(u^{2}+v^{2})}$ satisfies the hypotheses of Theorem 3.1. To say that the two limits in Theorem 3.1 are equal implies, in particular, that they exist. The fact that
$f(v)=\frac{v}{2(u^{2}+v^{2})}$ satisfies the hypotheses of Theorem 3.1. To say that the two limits in Theorem 3.1 are equal implies, in particular, that they exist. The fact that ![]() $\int _{0}^{\infty }g(x)\,dx$ exists can be seen, in particular, from Lemma 3.4. Together, we conclude that
$\int _{0}^{\infty }g(x)\,dx$ exists can be seen, in particular, from Lemma 3.4. Together, we conclude that ![]() $\sum _{m=1}^{\infty }g(m)$ is convergent. Employing Theorem 3.1 with
$\sum _{m=1}^{\infty }g(m)$ is convergent. Employing Theorem 3.1 with ![]() $f(v)=\frac{v}{2(u^{2}+v^{2})}$ and
$f(v)=\frac{v}{2(u^{2}+v^{2})}$ and ![]() $g(x)$ as in (3.24) and invoking Lemma 3.4, we see that
$g(x)$ as in (3.24) and invoking Lemma 3.4, we see that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{m=1}^{\infty }g(m) & = & \displaystyle \frac{1}{2}\lim _{M\rightarrow \infty }\biggl(\mathop{\sum }_{n=1}^{M}\frac{n}{u^{2}+n^{2}}-\int _{0}^{M}\frac{v}{u^{2}+v^{2}}\,dv\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\lim _{M\rightarrow \infty }\bigg\{\biggl(\mathop{\sum }_{n=1}^{M}\frac{n}{u^{2}+n^{2}}-\log M\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(\log M-\int _{0}^{M}\frac{v}{u^{2}+v^{2}}\,dv\biggr)\bigg\}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\biggl[-\frac{1}{2}(\unicode[STIX]{x1D713}(iu)+\unicode[STIX]{x1D713}(-iu))\biggr]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\lim _{M\rightarrow \infty }\biggl(\log M-\int _{0}^{M}\frac{v}{u^{2}+v^{2}}\,dv\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\biggl[-\frac{1}{2}(\unicode[STIX]{x1D713}(iu)+\unicode[STIX]{x1D713}(-iu))\biggr]+\frac{1}{2}\lim _{M\rightarrow \infty }\biggl(\log \frac{M}{\sqrt{u^{2}+M^{2}}}+\log u\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\biggl(\log u-\frac{1}{2}(\unicode[STIX]{x1D713}(iu)+\unicode[STIX]{x1D713}(-iu))\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{m=1}^{\infty }g(m) & = & \displaystyle \frac{1}{2}\lim _{M\rightarrow \infty }\biggl(\mathop{\sum }_{n=1}^{M}\frac{n}{u^{2}+n^{2}}-\int _{0}^{M}\frac{v}{u^{2}+v^{2}}\,dv\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\lim _{M\rightarrow \infty }\bigg\{\biggl(\mathop{\sum }_{n=1}^{M}\frac{n}{u^{2}+n^{2}}-\log M\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(\log M-\int _{0}^{M}\frac{v}{u^{2}+v^{2}}\,dv\biggr)\bigg\}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\biggl[-\frac{1}{2}(\unicode[STIX]{x1D713}(iu)+\unicode[STIX]{x1D713}(-iu))\biggr]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\lim _{M\rightarrow \infty }\biggl(\log M-\int _{0}^{M}\frac{v}{u^{2}+v^{2}}\,dv\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\biggl[-\frac{1}{2}(\unicode[STIX]{x1D713}(iu)+\unicode[STIX]{x1D713}(-iu))\biggr]+\frac{1}{2}\lim _{M\rightarrow \infty }\biggl(\log \frac{M}{\sqrt{u^{2}+M^{2}}}+\log u\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\biggl(\log u-\frac{1}{2}(\unicode[STIX]{x1D713}(iu)+\unicode[STIX]{x1D713}(-iu))\biggr),\end{eqnarray}$$ where in the third step, we used [Reference Dixit20, Equation (3.8)]. Theorem 2.2 now follows from (3.25) and by employing the change of variable ![]() $v=t/(2\unicode[STIX]{x1D70B}m)$ and replacing
$v=t/(2\unicode[STIX]{x1D70B}m)$ and replacing ![]() $x$ by
$x$ by ![]() $m$ and
$m$ and ![]() $u$ by
$u$ by ![]() $u/(2\unicode[STIX]{x1D70B})$.◻
$u/(2\unicode[STIX]{x1D70B})$.◻
Finally, Theorem 2.2 and Lemma 3.2 together give the following beautiful closed-form evaluation of a double sum. We record it as a separate theorem for its possible applicability in other studies.
Theorem 3.5. For ![]() $u>0$,
$u>0$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m=1}^{\infty }\mathop{\sum }_{k=0}^{\infty }\frac{(mu)^{2k}}{(2k)!}(\unicode[STIX]{x1D713}(2k+1)-\log (mu))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\bigg\{\log \biggl(\frac{u}{2\unicode[STIX]{x1D70B}}\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{iu}{2\unicode[STIX]{x1D70B}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-iu}{2\unicode[STIX]{x1D70B}}\biggr)\biggr)\bigg\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m=1}^{\infty }\mathop{\sum }_{k=0}^{\infty }\frac{(mu)^{2k}}{(2k)!}(\unicode[STIX]{x1D713}(2k+1)-\log (mu))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\bigg\{\log \biggl(\frac{u}{2\unicode[STIX]{x1D70B}}\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{iu}{2\unicode[STIX]{x1D70B}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-iu}{2\unicode[STIX]{x1D70B}}\biggr)\biggr)\bigg\}.\nonumber\end{eqnarray}$$Remark 8. A mere look at the double series on the left side above indicates that one cannot interchange the order of the double sum. This makes its closed-form evaluation all the more interesting.
4 Proof of the formula for the Hurwitz zeta function at rational arguments
We begin with a lemma which gives inverse Mellin transform of ![]() $\frac{\unicode[STIX]{x1D6E4}(s)}{\tan (\frac{\unicode[STIX]{x1D70B}s}{2})}$. It is crucial in proving Theorem 2.1. Here, and throughout the sequel, we use
$\frac{\unicode[STIX]{x1D6E4}(s)}{\tan (\frac{\unicode[STIX]{x1D70B}s}{2})}$. It is crucial in proving Theorem 2.1. Here, and throughout the sequel, we use ![]() $\int _{(c)}$ to denote
$\int _{(c)}$ to denote ![]() $\int _{c-i\infty }^{c+i\infty }$.
$\int _{c-i\infty }^{c+i\infty }$.
Lemma 4.1. For ![]() $0<\text{Re}(s)=c_{1}<2$ and
$0<\text{Re}(s)=c_{1}<2$ and ![]() $\text{Re}(u)>0$, we have
$\text{Re}(u)>0$, we have
Proof. For ![]() $0<\text{Re}(s)<1$, we have [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 1101, Formula (3)]
$0<\text{Re}(s)<1$, we have [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 1101, Formula (3)]
and for ![]() $0<\text{Re}(s)<2$, we have [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 1101, Formula (6)]
$0<\text{Re}(s)<2$, we have [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 1101, Formula (6)]
Using Parseval’s formula [Reference Paris and Kaminski52, page 83, Equation (3.1.13)], for ![]() $0<\text{Re}(s)<1$, one can obtain
$0<\text{Re}(s)<1$, one can obtain
 $$\begin{eqnarray}\displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s)}{\tan (\frac{\unicode[STIX]{x1D70B}s}{2})}u^{-s}\,\text{d}s & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s)\cos (\frac{\unicode[STIX]{x1D70B}s}{2})}{\sin (\frac{\unicode[STIX]{x1D70B}s}{2})}u^{-s}\,\text{d}s\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70B}}\int _{0}^{\infty }\frac{2\cos t}{1+\frac{u^{2}}{t^{2}}}\,\frac{\text{d}t}{t}\nonumber\\ \displaystyle & = & \displaystyle \frac{2}{\unicode[STIX]{x1D70B}}\int _{0}^{\infty }\frac{t\cos t}{u^{2}+t^{2}}\,\text{d}t.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s)}{\tan (\frac{\unicode[STIX]{x1D70B}s}{2})}u^{-s}\,\text{d}s & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s)\cos (\frac{\unicode[STIX]{x1D70B}s}{2})}{\sin (\frac{\unicode[STIX]{x1D70B}s}{2})}u^{-s}\,\text{d}s\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70B}}\int _{0}^{\infty }\frac{2\cos t}{1+\frac{u^{2}}{t^{2}}}\,\frac{\text{d}t}{t}\nonumber\\ \displaystyle & = & \displaystyle \frac{2}{\unicode[STIX]{x1D70B}}\int _{0}^{\infty }\frac{t\cos t}{u^{2}+t^{2}}\,\text{d}t.\nonumber\end{eqnarray}$$ Now one can easily extend the region of validity of the above result to ![]() $0<\text{Re}(s)<2$ by noting that when we shift the line of integration
$0<\text{Re}(s)<2$ by noting that when we shift the line of integration ![]() $\text{Re}(s)=c_{1}$ to, say,
$\text{Re}(s)=c_{1}$ to, say, ![]() $\text{Re}(s)=c_{2},1\leqslant c_{2}<2,$ one does not encounter any poles of the integrand, and also that the integrals over the horizontal segments tend to zero as the height
$\text{Re}(s)=c_{2},1\leqslant c_{2}<2,$ one does not encounter any poles of the integrand, and also that the integrals over the horizontal segments tend to zero as the height ![]() $T$ tends to
$T$ tends to ![]() $\infty$.◻
$\infty$.◻
Lemma 4.2. Let ![]() $N$ be an odd positive integer and
$N$ be an odd positive integer and ![]() $h>N/2$ be a positive integer. If
$h>N/2$ be a positive integer. If ![]() $\frac{N-2h+1}{N}=-2j$ for some
$\frac{N-2h+1}{N}=-2j$ for some ![]() $j\in \mathbb{N}$, then
$j\in \mathbb{N}$, then ![]() $j=\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$.
$j=\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$.
Proof. By hypothesis, ![]() $j+\frac{1}{2N}=\frac{h}{N}-\frac{1}{2}$. Since
$j+\frac{1}{2N}=\frac{h}{N}-\frac{1}{2}$. Since ![]() $j$ is an integer and
$j$ is an integer and ![]() $\lfloor \frac{1}{2N}\rfloor =0$ for
$\lfloor \frac{1}{2N}\rfloor =0$ for ![]() $N\geqslant 1$, we have
$N\geqslant 1$, we have ![]() $j=\lfloor j+\frac{1}{2N}\rfloor =\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$.◻
$j=\lfloor j+\frac{1}{2N}\rfloor =\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$.◻
The following lemma is well known and hence a proof is omitted.
Lemma 4.3. For any ![]() $z\in \mathbb{C}$ and
$z\in \mathbb{C}$ and ![]() $N\in \mathbb{N}$,
$N\in \mathbb{N}$,
 $$\begin{eqnarray}\frac{\sin (Nz)}{\sin (z)}=\sum _{j=-(N-1)}^{N-1}\exp (ijz),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\sin (Nz)}{\sin (z)}=\sum _{j=-(N-1)}^{N-1}\exp (ijz),\end{eqnarray}$$ where ![]() $^{\prime \prime }$ implies summation over
$^{\prime \prime }$ implies summation over ![]() $j=-(N-1),-(N-3),\ldots ,N-3,N-1$. Thus,
$j=-(N-1),-(N-3),\ldots ,N-3,N-1$. Thus,
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\cos (Nz)}{\cos (z)}=(-1)^{\frac{N-1}{2}}\sum _{j=-(N-1)}^{N-1}i^{j}\exp (-ijz)\quad (\text{for }N\text{ odd}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\cos (Nz)}{\cos (z)}=(-1)^{\frac{N-1}{2}}\sum _{j=-(N-1)}^{N-1}i^{j}\exp (-ijz)\quad (\text{for }N\text{ odd}), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\sin (Nz)}{\cos (z)}=(-1)^{\frac{N}{2}}\sum _{j=-(N-1)}^{N-1}i^{j}\exp (ijz)\quad (\text{for }N\text{ even}). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\sin (Nz)}{\cos (z)}=(-1)^{\frac{N}{2}}\sum _{j=-(N-1)}^{N-1}i^{j}\exp (ijz)\quad (\text{for }N\text{ even}). & \displaystyle\end{eqnarray}$$We have now collected all tools necessary for proving Theorem 2.1.
Proof of Theorem 2.1.
The hypothesis ![]() $h\geqslant N/2$,
$h\geqslant N/2$, ![]() $N\in \mathbb{N}$, will be used several times, without mention, in the proof. It is easy to see that the series
$N\in \mathbb{N}$, will be used several times, without mention, in the proof. It is easy to see that the series ![]() $\sum _{n=0}^{\infty }n^{N-2h}\frac{\exp (-an^{N}x)}{1-\exp (-n^{N}x)}$ is absolutely and uniformly convergent for any
$\sum _{n=0}^{\infty }n^{N-2h}\frac{\exp (-an^{N}x)}{1-\exp (-n^{N}x)}$ is absolutely and uniformly convergent for any ![]() $x>0,N\in \mathbb{N}$. Thus, interchanging the order of summation and integration in the first step below, we see that for
$x>0,N\in \mathbb{N}$. Thus, interchanging the order of summation and integration in the first step below, we see that for ![]() $\text{Re}(s)>\max (\frac{N-2h+1}{N},1)=1$,
$\text{Re}(s)>\max (\frac{N-2h+1}{N},1)=1$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }x^{s-1}\mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\exp (-an^{N}x)}{1-\exp (-n^{N}x)}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=1}^{\infty }n^{N-2h}\int _{0}^{\infty }x^{s-1}\frac{\exp (-an^{N}x)}{1-\exp (-n^{N}x)}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=1}^{\infty }n^{N-2h-Ns}\int _{0}^{\infty }\frac{y^{s-1}e^{-ay}}{1-e^{-y}}\,\text{d}y\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-N+2h),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }x^{s-1}\mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\exp (-an^{N}x)}{1-\exp (-n^{N}x)}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=1}^{\infty }n^{N-2h}\int _{0}^{\infty }x^{s-1}\frac{\exp (-an^{N}x)}{1-\exp (-n^{N}x)}\,\text{d}x\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=1}^{\infty }n^{N-2h-Ns}\int _{0}^{\infty }\frac{y^{s-1}e^{-ay}}{1-e^{-y}}\,\text{d}y\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-N+2h),\nonumber\end{eqnarray}$$ where, in the second step, we employed the change of variable ![]() $y=n^{N}x$ and in the third, we used the fact [Reference Apostol5, page 251, Theorem 12.2] that for
$y=n^{N}x$ and in the third, we used the fact [Reference Apostol5, page 251, Theorem 12.2] that for ![]() $\text{Re}(s)>1$,
$\text{Re}(s)>1$,
Thus, for ![]() $\unicode[STIX]{x1D706}=\text{Re}(s)>1$,
$\unicode[STIX]{x1D706}=\text{Re}(s)>1$,
We now obtain an alternate evaluation of the above integral by shifting the line of integration and then using Cauchy’s residue theorem. Consider the contour ![]() ${\mathcal{C}}$ determined by the line segments
${\mathcal{C}}$ determined by the line segments ![]() $[\unicode[STIX]{x1D706}-iT,\unicode[STIX]{x1D706}+iT],[\unicode[STIX]{x1D706}+iT,-r+iT],[-r+iT,-r-iT]$ and
$[\unicode[STIX]{x1D706}-iT,\unicode[STIX]{x1D706}+iT],[\unicode[STIX]{x1D706}+iT,-r+iT],[-r+iT,-r-iT]$ and ![]() $[-r-iT,\unicode[STIX]{x1D706}-iT]$, where,
$[-r-iT,\unicode[STIX]{x1D706}-iT]$, where, ![]() $r$ is a sufficiently large positive real number which is not an integer and
$r$ is a sufficiently large positive real number which is not an integer and ![]() $\frac{2h}{N}-1<r<\frac{2h+1}{N}-1$. The reason for choosing the lower and upper bounds for
$\frac{2h}{N}-1<r<\frac{2h+1}{N}-1$. The reason for choosing the lower and upper bounds for ![]() $r$ will be explained soon. Let
$r$ will be explained soon. Let
and let ![]() $R_{a}$ denote the residue of
$R_{a}$ denote the residue of ![]() $F(s)$ at the pole
$F(s)$ at the pole ![]() $s=a$. We first find the poles of
$s=a$. We first find the poles of ![]() $F(s)$ and residues at those poles.
$F(s)$ and residues at those poles.
(1) ![]() $F(s)$ has a simple pole at
$F(s)$ has a simple pole at ![]() $s=0$ since
$s=0$ since ![]() $\unicode[STIX]{x1D6E4}(s)$ has a simple pole at
$\unicode[STIX]{x1D6E4}(s)$ has a simple pole at ![]() $s=0$ with the residue
$s=0$ with the residue
since from [Reference Apostol5, page 264, Theorem 12.13], ![]() $\unicode[STIX]{x1D701}(-n,a)=-\frac{B_{n+1}(a)}{n+1},n\geqslant 0$ and
$\unicode[STIX]{x1D701}(-n,a)=-\frac{B_{n+1}(a)}{n+1},n\geqslant 0$ and ![]() $B_{1}(a)=a-\frac{1}{2}$.
$B_{1}(a)=a-\frac{1}{2}$.
(2) Since ![]() $\unicode[STIX]{x1D701}(s,a)$ has a simple pole at
$\unicode[STIX]{x1D701}(s,a)$ has a simple pole at ![]() $s=1$,
$s=1$, ![]() $F(s)$ has a simple pole at
$F(s)$ has a simple pole at ![]() $s=1$ with residue
$s=1$ with residue
(3) Since ![]() $\frac{N-2h+1}{N}\neq -2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, Lemma 4.2 implies
$\frac{N-2h+1}{N}\neq -2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, Lemma 4.2 implies ![]() $\frac{N-2h+1}{N}\neq -2j$ for any
$\frac{N-2h+1}{N}\neq -2j$ for any ![]() $j\geqslant 1$. Thus,
$j\geqslant 1$. Thus, ![]() $F(s)$ has a simple pole at
$F(s)$ has a simple pole at ![]() $s=\frac{N-2h+1}{N}$, owing to the pole of
$s=\frac{N-2h+1}{N}$, owing to the pole of ![]() $\unicode[STIX]{x1D701}(s)$ at
$\unicode[STIX]{x1D701}(s)$ at ![]() $s=1$, with the residue
$s=1$, with the residue
(4) Consider the simple poles of ![]() $\unicode[STIX]{x1D6E4}(s)$ at
$\unicode[STIX]{x1D6E4}(s)$ at ![]() $s=-2j,j\in \mathbb{N}$, and the trivial zeros of
$s=-2j,j\in \mathbb{N}$, and the trivial zeros of ![]() $\unicode[STIX]{x1D701}(Ns-N+2h)$ at
$\unicode[STIX]{x1D701}(Ns-N+2h)$ at ![]() $-2k,k\in \mathbb{N}$. It is important to see if some of these poles of
$-2k,k\in \mathbb{N}$. It is important to see if some of these poles of ![]() $\unicode[STIX]{x1D6E4}(s)$ get canceled by the trivial zeros of
$\unicode[STIX]{x1D6E4}(s)$ get canceled by the trivial zeros of ![]() $\unicode[STIX]{x1D701}(Ns-N+2h)$. To that end, suppose for some positive integers
$\unicode[STIX]{x1D701}(Ns-N+2h)$. To that end, suppose for some positive integers ![]() $j^{\prime }$ and
$j^{\prime }$ and ![]() $k^{\prime }$ we have
$k^{\prime }$ we have ![]() $N(-2j^{\prime })-N+2h=-2k^{\prime }$. Then
$N(-2j^{\prime })-N+2h=-2k^{\prime }$. Then ![]() $k^{\prime }=Nj^{\prime }+\frac{N}{2}-h$. This implies that if
$k^{\prime }=Nj^{\prime }+\frac{N}{2}-h$. This implies that if ![]() $N$ is an odd positive integer, no pole of
$N$ is an odd positive integer, no pole of ![]() $\unicode[STIX]{x1D6E4}(s)$ at a negative even integer will get canceled by a trivial zero of
$\unicode[STIX]{x1D6E4}(s)$ at a negative even integer will get canceled by a trivial zero of ![]() $\unicode[STIX]{x1D701}(Ns-N+2h)$ since
$\unicode[STIX]{x1D701}(Ns-N+2h)$ since ![]() $k^{\prime }$ is not an integer. However, if
$k^{\prime }$ is not an integer. However, if ![]() $N$ is an even positive integer, then
$N$ is an even positive integer, then ![]() $k^{\prime }$ can equal
$k^{\prime }$ can equal ![]() $Nj^{\prime }+\frac{N}{2}-h$, while being a positive integer, implying
$Nj^{\prime }+\frac{N}{2}-h$, while being a positive integer, implying ![]() $j^{\prime }>\frac{h}{N}-\frac{1}{2}$, that is, among the poles of
$j^{\prime }>\frac{h}{N}-\frac{1}{2}$, that is, among the poles of ![]() $\unicode[STIX]{x1D6E4}(s)$ at negative even integers, only the poles
$\unicode[STIX]{x1D6E4}(s)$ at negative even integers, only the poles ![]() $-2j$,
$-2j$, ![]() $1\leqslant j\leqslant \lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, contribute toward the evaluation of the line integral. To sum up, when
$1\leqslant j\leqslant \lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, contribute toward the evaluation of the line integral. To sum up, when ![]() $N$ is odd integer,
$N$ is odd integer, ![]() $F(s)$ has simple poles at all negative even integers
$F(s)$ has simple poles at all negative even integers ![]() $-2j,j\geqslant 1$, and when
$-2j,j\geqslant 1$, and when ![]() $N$ is an even integer,
$N$ is an even integer, ![]() $F(s)$ has simple poles at
$F(s)$ has simple poles at ![]() $-2j$, where
$-2j$, where ![]() $1\leqslant j\leqslant \lfloor \frac{h}{N}-\frac{1}{2}\rfloor$. The residue at such a pole is
$1\leqslant j\leqslant \lfloor \frac{h}{N}-\frac{1}{2}\rfloor$. The residue at such a pole is
 $$\begin{eqnarray}\displaystyle R_{-2j} & = & \displaystyle \lim _{s\rightarrow -2j}(s+2j)\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))x^{-s}\nonumber\\ \displaystyle & = & \displaystyle -\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(-2jN-N+2h)x^{2j}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{-2j} & = & \displaystyle \lim _{s\rightarrow -2j}(s+2j)\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))x^{-s}\nonumber\\ \displaystyle & = & \displaystyle -\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(-2jN-N+2h)x^{2j}.\end{eqnarray}$$ At this juncture, it deems necessary to explain why we choose the real part of the shifted line of integration to be ![]() $-r$ with
$-r$ with ![]() $r>\frac{2h}{N}-1$. The reason is, this implies
$r>\frac{2h}{N}-1$. The reason is, this implies ![]() $-r<-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, and thus all poles of
$-r<-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, and thus all poles of ![]() $\unicode[STIX]{x1D6E4}(s)$ at negative even integers
$\unicode[STIX]{x1D6E4}(s)$ at negative even integers ![]() $-2j$, where
$-2j$, where ![]() $1\leqslant j\leqslant \lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, lie inside the contour, thus contributing toward the evaluation of the line integral.
$1\leqslant j\leqslant \lfloor \frac{h}{N}-\frac{1}{2}\rfloor$, lie inside the contour, thus contributing toward the evaluation of the line integral.
(5) Arguing as in (4), it can be seen that ![]() $F(s)$ has simple poles at
$F(s)$ has simple poles at ![]() $s=-(2j-1)$,
$s=-(2j-1)$, ![]() $1\leqslant j\leqslant \lfloor \frac{h}{N}\rfloor$, and the residue at such a pole is
$1\leqslant j\leqslant \lfloor \frac{h}{N}\rfloor$, and the residue at such a pole is
 $$\begin{eqnarray}\displaystyle R_{-(2j-1)} & = & \displaystyle \lim _{s\rightarrow -(2j-1)}(s+(2j-1))F(s)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{h+1}2^{2h-1}\unicode[STIX]{x1D70B}^{2h}\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{2h-2jN}}{(2j)!(2h-2jN)!}x^{2j-1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{-(2j-1)} & = & \displaystyle \lim _{s\rightarrow -(2j-1)}(s+(2j-1))F(s)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{h+1}2^{2h-1}\unicode[STIX]{x1D70B}^{2h}\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{2h-2jN}}{(2j)!(2h-2jN)!}x^{2j-1}.\end{eqnarray}$$Now applying Cauchy’s residue theorem, we observe that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\biggl[\int _{\unicode[STIX]{x1D706}-iT}^{\unicode[STIX]{x1D706}+iT}+\int _{\unicode[STIX]{x1D706}+iT}^{-r+iT}+\int _{-r+iT}^{-r-iT}+\int _{-r-iT}^{\unicode[STIX]{x1D706}-iT}\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{\unicode[STIX]{x1D6E4}(s)}{x^{s}}\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle \quad =R_{0}+R_{1}+R_{\frac{N-2h+1}{N}}+\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}\rfloor }R_{-(2j-1)}+\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }R_{-2j}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\biggl[\int _{\unicode[STIX]{x1D706}-iT}^{\unicode[STIX]{x1D706}+iT}+\int _{\unicode[STIX]{x1D706}+iT}^{-r+iT}+\int _{-r+iT}^{-r-iT}+\int _{-r-iT}^{\unicode[STIX]{x1D706}-iT}\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{\unicode[STIX]{x1D6E4}(s)}{x^{s}}\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle \quad =R_{0}+R_{1}+R_{\frac{N-2h+1}{N}}+\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}\rfloor }R_{-(2j-1)}+\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }R_{-2j}.\nonumber\end{eqnarray}$$ Now let ![]() $T\rightarrow \infty$. Using Stirling’s formula for
$T\rightarrow \infty$. Using Stirling’s formula for ![]() $\unicode[STIX]{x1D6E4}(s)$ and elementary bounds on the Riemann zeta function and the Hurwitz zeta function, it can be seen that the integrals along the horizontal segments
$\unicode[STIX]{x1D6E4}(s)$ and elementary bounds on the Riemann zeta function and the Hurwitz zeta function, it can be seen that the integrals along the horizontal segments ![]() $[\unicode[STIX]{x1D706}+iT,-r+iT]$,
$[\unicode[STIX]{x1D706}+iT,-r+iT]$, ![]() $[-r-iT,\unicode[STIX]{x1D706}-iT]$ approach zero as
$[-r-iT,\unicode[STIX]{x1D706}-iT]$ approach zero as ![]() $T\rightarrow \infty$. Hence from (4.6)–(4.10),
$T\rightarrow \infty$. Hence from (4.6)–(4.10),
where ![]() $P(x,a)$ is the sum of all residues of
$P(x,a)$ is the sum of all residues of ![]() $F(s)$, defined in (2.2), and
$F(s)$, defined in (2.2), and
It remains to show that ![]() $J(x,a)$ agrees with
$J(x,a)$ agrees with ![]() $S(x,a)$ defined in (2.3) and (2.4) respectively when
$S(x,a)$ defined in (2.3) and (2.4) respectively when ![]() $N$ is odd and even. To evaluate
$N$ is odd and even. To evaluate ![]() $J(x,a)$, we first make a change of variable
$J(x,a)$, we first make a change of variable ![]() $s\leftrightarrow 1-s$ in (4.12) so that
$s\leftrightarrow 1-s$ in (4.12) so that
Now replace ![]() $s$ by
$s$ by ![]() $1-s$ in (1.4), then multiply both sides of the resulting identity by
$1-s$ in (1.4), then multiply both sides of the resulting identity by ![]() $\unicode[STIX]{x1D6E4}(1-s)$ to obtain, for
$\unicode[STIX]{x1D6E4}(1-s)$ to obtain, for ![]() $\text{Re}(s)>1$,
$\text{Re}(s)>1$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E4}(1-s)\unicode[STIX]{x1D701}(1-s,a)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2\unicode[STIX]{x1D6E4}(1-s)\unicode[STIX]{x1D6E4}(s)}{(2\unicode[STIX]{x1D70B})^{s}}\bigg\{\cos \biggl(\frac{\unicode[STIX]{x1D70B}s}{2}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{s}}+\sin \biggl(\frac{\unicode[STIX]{x1D70B}s}{2}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{s}}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =(2\unicode[STIX]{x1D70B})^{1-s}\bigg\{\frac{1}{2\sin (\frac{\unicode[STIX]{x1D70B}s}{2})}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{s}}+\frac{1}{2\cos (\frac{\unicode[STIX]{x1D70B}s}{2})}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{s}}\bigg\},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E4}(1-s)\unicode[STIX]{x1D701}(1-s,a)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2\unicode[STIX]{x1D6E4}(1-s)\unicode[STIX]{x1D6E4}(s)}{(2\unicode[STIX]{x1D70B})^{s}}\bigg\{\cos \biggl(\frac{\unicode[STIX]{x1D70B}s}{2}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{s}}+\sin \biggl(\frac{\unicode[STIX]{x1D70B}s}{2}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{s}}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =(2\unicode[STIX]{x1D70B})^{1-s}\bigg\{\frac{1}{2\sin (\frac{\unicode[STIX]{x1D70B}s}{2})}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{s}}+\frac{1}{2\cos (\frac{\unicode[STIX]{x1D70B}s}{2})}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{s}}\bigg\},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$where in the last step, we used the reflection formula for the gamma function.
We note here that Kanemitsu et al. [Reference Kanemitsu, Tanigawa and Yoshimoto37, page 51] use a formula equivalent to (1.4), namely, for ![]() $\text{Re}(s)<0$,
$\text{Re}(s)<0$,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s,a) & = & \displaystyle \frac{\unicode[STIX]{x1D6E4}(1-s)}{(2\unicode[STIX]{x1D70B})^{1-s}}\biggl(\exp \biggl(\frac{-\unicode[STIX]{x1D70B}i(1-s)}{2}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{e^{2\unicode[STIX]{x1D70B}ian}}{n^{1-s}}\nonumber\\ \displaystyle & & \displaystyle +\,\exp \biggl(\frac{\unicode[STIX]{x1D70B}i(1-s)}{2}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{e^{-2\unicode[STIX]{x1D70B}ian}}{n^{1-s}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s,a) & = & \displaystyle \frac{\unicode[STIX]{x1D6E4}(1-s)}{(2\unicode[STIX]{x1D70B})^{1-s}}\biggl(\exp \biggl(\frac{-\unicode[STIX]{x1D70B}i(1-s)}{2}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{e^{2\unicode[STIX]{x1D70B}ian}}{n^{1-s}}\nonumber\\ \displaystyle & & \displaystyle +\,\exp \biggl(\frac{\unicode[STIX]{x1D70B}i(1-s)}{2}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{e^{-2\unicode[STIX]{x1D70B}ian}}{n^{1-s}}\biggr).\nonumber\end{eqnarray}$$ However, one can see that while the above formula is useful when ![]() $N$ is an even positive integer, it is not when
$N$ is an even positive integer, it is not when ![]() $N$ is odd. In fact, employing it leads to very complicated integrals which do not seem to lead us to any concrete result. On the other hand, (1.4) works for any positive integer
$N$ is odd. In fact, employing it leads to very complicated integrals which do not seem to lead us to any concrete result. On the other hand, (1.4) works for any positive integer ![]() $N$, irrespective of its parity, as will be seen in the remainder of the proof.
$N$, irrespective of its parity, as will be seen in the remainder of the proof.
Now substitute (4.14) in (4.13) and invoke the functional equation [Reference Apostol5, page 259] ![]() $\unicode[STIX]{x1D701}(w)=2^{w}\unicode[STIX]{x1D70B}^{w-1}\unicode[STIX]{x1D6E4}(1-w)\unicode[STIX]{x1D701}(1-w)\sin (\frac{1}{2}\unicode[STIX]{x1D70B}w)$ for
$\unicode[STIX]{x1D701}(w)=2^{w}\unicode[STIX]{x1D70B}^{w-1}\unicode[STIX]{x1D6E4}(1-w)\unicode[STIX]{x1D701}(1-w)\sin (\frac{1}{2}\unicode[STIX]{x1D70B}w)$ for ![]() $\unicode[STIX]{x1D701}(2h-Ns)$ to obtain after simplification
$\unicode[STIX]{x1D701}(2h-Ns)$ to obtain after simplification
where
 $$\begin{eqnarray}\displaystyle J_{1}(x,a) & := & \displaystyle \frac{(-1)^{h+1}2^{2h+1}\unicode[STIX]{x1D70B}^{2h}}{x}\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(1+r)}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{-s}\unicode[STIX]{x1D6E4}(1-2h+Ns)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(1-2h+Ns)\bigg\{\frac{\sin (\frac{N\unicode[STIX]{x1D70B}s}{2})}{2\sin (\frac{\unicode[STIX]{x1D70B}s}{2})}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{s}}\bigg\}\,\text{d}s,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{1}(x,a) & := & \displaystyle \frac{(-1)^{h+1}2^{2h+1}\unicode[STIX]{x1D70B}^{2h}}{x}\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(1+r)}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{-s}\unicode[STIX]{x1D6E4}(1-2h+Ns)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(1-2h+Ns)\bigg\{\frac{\sin (\frac{N\unicode[STIX]{x1D70B}s}{2})}{2\sin (\frac{\unicode[STIX]{x1D70B}s}{2})}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{s}}\bigg\}\,\text{d}s,\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle J_{2}(x,a) & := & \displaystyle \frac{(-1)^{h+1}2^{2h+1}\unicode[STIX]{x1D70B}^{2h}}{x}\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(1+r)}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{-s}\unicode[STIX]{x1D6E4}(1-2h+Ns)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(1-2h+Ns)\bigg\{\frac{\sin (\frac{N\unicode[STIX]{x1D70B}s}{2})}{2\cos (\frac{\unicode[STIX]{x1D70B}s}{2})}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{s}}\bigg\}\,\text{d}s.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{2}(x,a) & := & \displaystyle \frac{(-1)^{h+1}2^{2h+1}\unicode[STIX]{x1D70B}^{2h}}{x}\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(1+r)}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{-s}\unicode[STIX]{x1D6E4}(1-2h+Ns)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(1-2h+Ns)\bigg\{\frac{\sin (\frac{N\unicode[STIX]{x1D70B}s}{2})}{2\cos (\frac{\unicode[STIX]{x1D70B}s}{2})}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{s}}\bigg\}\,\text{d}s.\end{eqnarray}$$ We first evaluate ![]() $J_{2}(x,a)$. Its evaluation depends on the parity of
$J_{2}(x,a)$. Its evaluation depends on the parity of ![]() $N$. Assume first that
$N$. Assume first that ![]() $N$ is odd. Employ the change of variable
$N$ is odd. Employ the change of variable
in (4.17) so that ![]() $c_{1}:=\text{Re}(s_{1})>1$ (since
$c_{1}:=\text{Re}(s_{1})>1$ (since ![]() $r>\frac{2h}{N}-1$), write
$r>\frac{2h}{N}-1$), write ![]() $\unicode[STIX]{x1D701}(s_{1})=\sum _{m=1}^{\infty }m^{-s_{1}}$, and then interchange the order of double sum and the integral, permitted because of absolute convergence, to arrive at
$\unicode[STIX]{x1D701}(s_{1})=\sum _{m=1}^{\infty }m^{-s_{1}}$, and then interchange the order of double sum and the integral, permitted because of absolute convergence, to arrive at
 $$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle \frac{(-1)^{h+1}2^{2h+1}\unicode[STIX]{x1D70B}^{2h}}{Nx}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{\frac{1-2h}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{m,n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)E(X_{m,n}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle \frac{(-1)^{h+1}2^{2h+1}\unicode[STIX]{x1D70B}^{2h}}{Nx}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{\frac{1-2h}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{m,n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)E(X_{m,n}),\end{eqnarray}$$where
with
Using (4.2) in the second step below, we find that
 $$\begin{eqnarray}\displaystyle E(X_{m,n}) & = & \displaystyle \frac{-1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s_{1})}{2\tan (\frac{\unicode[STIX]{x1D70B}s_{1}}{2})}\frac{\cos (\frac{\unicode[STIX]{x1D70B}}{2}(s_{1}+2h-1))}{\cos (\frac{\unicode[STIX]{x1D70B}}{2}(\frac{s_{1}+2h-1}{N}))}X_{m,n}^{-s_{1}}\,\text{d}s_{1}\nonumber\\ \displaystyle & = & \displaystyle \frac{(-1)^{\frac{N+1}{2}}}{2}\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s_{1})}{\tan (\frac{\unicode[STIX]{x1D70B}s_{1}}{2})}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{j=-(N-1)}^{N-1}i^{j}e^{-\frac{ij\unicode[STIX]{x1D70B}}{2}(\frac{s_{1}+2h-1}{N})}X_{m,n}^{-s_{1}}\,\text{d}s_{1}\nonumber\\ \displaystyle & = & \displaystyle \frac{(-1)^{\frac{N+1}{2}}}{2}\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s_{1})}{\tan (\frac{\unicode[STIX]{x1D70B}s_{1}}{2})}{X_{m,n,j}^{\ast }}^{-s_{1}}\,\text{d}s_{1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E(X_{m,n}) & = & \displaystyle \frac{-1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s_{1})}{2\tan (\frac{\unicode[STIX]{x1D70B}s_{1}}{2})}\frac{\cos (\frac{\unicode[STIX]{x1D70B}}{2}(s_{1}+2h-1))}{\cos (\frac{\unicode[STIX]{x1D70B}}{2}(\frac{s_{1}+2h-1}{N}))}X_{m,n}^{-s_{1}}\,\text{d}s_{1}\nonumber\\ \displaystyle & = & \displaystyle \frac{(-1)^{\frac{N+1}{2}}}{2}\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s_{1})}{\tan (\frac{\unicode[STIX]{x1D70B}s_{1}}{2})}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{j=-(N-1)}^{N-1}i^{j}e^{-\frac{ij\unicode[STIX]{x1D70B}}{2}(\frac{s_{1}+2h-1}{N})}X_{m,n}^{-s_{1}}\,\text{d}s_{1}\nonumber\\ \displaystyle & = & \displaystyle \frac{(-1)^{\frac{N+1}{2}}}{2}\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s_{1})}{\tan (\frac{\unicode[STIX]{x1D70B}s_{1}}{2})}{X_{m,n,j}^{\ast }}^{-s_{1}}\,\text{d}s_{1},\end{eqnarray}$$where
Now (4.18) and the inequality ![]() $\frac{2h}{N}-1<r<\frac{2h+1}{N}-1$ along with the fact that
$\frac{2h}{N}-1<r<\frac{2h+1}{N}-1$ along with the fact that ![]() $\text{Re}(s)=1+r$ imply that
$\text{Re}(s)=1+r$ imply that ![]() $1<\text{Re}(s_{1})<2$. The reason why we initially chose
$1<\text{Re}(s_{1})<2$. The reason why we initially chose ![]() $r<\frac{2h+1}{N}-1$ is because, we need
$r<\frac{2h+1}{N}-1$ is because, we need ![]() $\text{Re}(s_{1})<2$ in order to use Lemma 4.1. Hence invoking Lemma 4.1 to simplify the above representation for
$\text{Re}(s_{1})<2$ in order to use Lemma 4.1. Hence invoking Lemma 4.1 to simplify the above representation for ![]() $E(X_{m,n})$ and then substituting the resultant in (4.19) gives
$E(X_{m,n})$ and then substituting the resultant in (4.19) gives
 $$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle \frac{2}{\unicode[STIX]{x1D70B}Nx}(-1)^{h+\frac{N+3}{2}}(2\unicode[STIX]{x1D70B})^{2h}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{\frac{1-2h}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)\mathop{\sum }_{m=1}^{\infty }\int _{0}^{\infty }\frac{t\cos (t)}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,\text{d}t.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle \frac{2}{\unicode[STIX]{x1D70B}Nx}(-1)^{h+\frac{N+3}{2}}(2\unicode[STIX]{x1D70B})^{2h}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{\frac{1-2h}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)\mathop{\sum }_{m=1}^{\infty }\int _{0}^{\infty }\frac{t\cos (t)}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,\text{d}t.\nonumber\end{eqnarray}$$ Now note that ![]() $\text{Re}(X_{m,n,j}^{\ast })=2\unicode[STIX]{x1D70B}m(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{N}}\cos (\frac{\unicode[STIX]{x1D70B}j}{2N})>0$ as
$\text{Re}(X_{m,n,j}^{\ast })=2\unicode[STIX]{x1D70B}m(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{N}}\cos (\frac{\unicode[STIX]{x1D70B}j}{2N})>0$ as
Hence apply Theorem 2.2 and then replace ![]() $j$ by
$j$ by ![]() $2j$ in the second step below to deduce that
$2j$ in the second step below to deduce that
 $$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle (-1)^{h+\frac{N+3}{2}}\frac{(2\unicode[STIX]{x1D70B})^{2h}}{\unicode[STIX]{x1D70B}Nx}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{\frac{1-2h}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)\bigg\{\log \biggl(\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{2N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(i\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{2N}}\biggr)+\unicode[STIX]{x1D713}\biggl(-i\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{2N}}\biggr)\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle =\frac{(-1)^{h+\frac{N+3}{2}}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\text{exp}\biggl(\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\bigg\{\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\bigg\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle (-1)^{h+\frac{N+3}{2}}\frac{(2\unicode[STIX]{x1D70B})^{2h}}{\unicode[STIX]{x1D70B}Nx}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{\frac{1-2h}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)\bigg\{\log \biggl(\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{2N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(i\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{2N}}\biggr)+\unicode[STIX]{x1D713}\biggl(-i\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{2N}}\biggr)\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle =\frac{(-1)^{h+\frac{N+3}{2}}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\text{exp}\biggl(\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\bigg\{\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\bigg\},\end{eqnarray}$$ where ![]() $A_{N,j}(y)=\unicode[STIX]{x1D70B}(2\unicode[STIX]{x1D70B}y)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}$. This completes the evaluation of
$A_{N,j}(y)=\unicode[STIX]{x1D70B}(2\unicode[STIX]{x1D70B}y)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}$. This completes the evaluation of ![]() $J_{2}(x,a)$ when
$J_{2}(x,a)$ when ![]() $N$ is odd.
$N$ is odd.
Now consider the case when ![]() $N$ is even. Note that (4.19) still holds with
$N$ is even. Note that (4.19) still holds with ![]() $E(X_{m,n})$ and
$E(X_{m,n})$ and ![]() $X_{m,n}$ defined in (4.20) and (4.21). Use (4.3) and (4.23) in the second step below to simplify
$X_{m,n}$ defined in (4.20) and (4.21). Use (4.3) and (4.23) in the second step below to simplify ![]() $E(X_{m,n})$ as
$E(X_{m,n})$ as
 $$\begin{eqnarray}\displaystyle E(X_{m,n}) & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s_{1})\sin (\frac{\unicode[STIX]{x1D70B}}{2}(s_{1}+2h-1))}{2\cos (\frac{\unicode[STIX]{x1D70B}}{2}(\frac{s_{1}+2h-1}{N}))}X_{m,n}^{-s_{1}}\,\text{d}s_{1}\nonumber\\ \displaystyle & = & \displaystyle \frac{(-1)^{\frac{N}{2}}}{2\unicode[STIX]{x1D70B}i}\sum _{j=-(N-1)}^{N-1}i^{j}\exp \biggl(\frac{i\unicode[STIX]{x1D70B}j(2h-1)}{2N}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{(c_{1})}\unicode[STIX]{x1D6E4}(s_{1}){X_{m,n,-j}^{\ast }}^{-s_{1}}\,\text{d}s_{1}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\frac{N}{2}}\sum _{j=-(N-1)}^{N-1}i^{j}\exp \biggl(\frac{i\unicode[STIX]{x1D70B}j(2h-1)}{2N}\biggr)e^{-X_{m,n,-j}^{\ast }},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E(X_{m,n}) & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(c_{1})}\frac{\unicode[STIX]{x1D6E4}(s_{1})\sin (\frac{\unicode[STIX]{x1D70B}}{2}(s_{1}+2h-1))}{2\cos (\frac{\unicode[STIX]{x1D70B}}{2}(\frac{s_{1}+2h-1}{N}))}X_{m,n}^{-s_{1}}\,\text{d}s_{1}\nonumber\\ \displaystyle & = & \displaystyle \frac{(-1)^{\frac{N}{2}}}{2\unicode[STIX]{x1D70B}i}\sum _{j=-(N-1)}^{N-1}i^{j}\exp \biggl(\frac{i\unicode[STIX]{x1D70B}j(2h-1)}{2N}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{(c_{1})}\unicode[STIX]{x1D6E4}(s_{1}){X_{m,n,-j}^{\ast }}^{-s_{1}}\,\text{d}s_{1}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\frac{N}{2}}\sum _{j=-(N-1)}^{N-1}i^{j}\exp \biggl(\frac{i\unicode[STIX]{x1D70B}j(2h-1)}{2N}\biggr)e^{-X_{m,n,-j}^{\ast }},\end{eqnarray}$$ since ![]() $\text{Re}(X_{m,n,-j}^{\ast })>0$, where in the last step, we used the inverse Mellin transform of
$\text{Re}(X_{m,n,-j}^{\ast })>0$, where in the last step, we used the inverse Mellin transform of ![]() $\unicode[STIX]{x1D6E4}(s_{1})$. Replace
$\unicode[STIX]{x1D6E4}(s_{1})$. Replace ![]() $j$ by
$j$ by ![]() $-2j-1$ in (4.25), then substitute the resultant in (4.19) to get
$-2j-1$ in (4.25), then substitute the resultant in (4.19) to get
 $$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle \frac{i(-1)^{h+\frac{N}{2}}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}(-1)^{j}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)(1-2h)}{2N}}\mathop{\sum }_{n=1}^{\infty }\frac{n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)}{\exp (2A_{N,j+\frac{1}{2}}(\frac{n}{x}))-1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle \frac{i(-1)^{h+\frac{N}{2}}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}(-1)^{j}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)(1-2h)}{2N}}\mathop{\sum }_{n=1}^{\infty }\frac{n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)}{\exp (2A_{N,j+\frac{1}{2}}(\frac{n}{x}))-1}.\end{eqnarray}$$ From (4.24) and (4.26), we obtain an expression for ![]() $J_{2}(x,a)$ for all positive integers
$J_{2}(x,a)$ for all positive integers ![]() $N$.
$N$.
Now ![]() $J_{1}(x,a)$ from (4.16) can be evaluated in a similar way to obtain
$J_{1}(x,a)$ from (4.16) can be evaluated in a similar way to obtain
 $$\begin{eqnarray}\displaystyle J_{1}(x,a) & = & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j}(\frac{n}{x}))-1)}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{1}(x,a) & = & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j}(\frac{n}{x}))-1)}\end{eqnarray}$$ for ![]() $N$ odd, whereas, for
$N$ odd, whereas, for ![]() $N$ even,
$N$ even,
 $$\begin{eqnarray}\displaystyle J_{1}(x,a) & = & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)(j+\frac{1}{2})}{N}}\nonumber\\ \displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j+\frac{1}{2}}(\frac{n}{x}))-1)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{1}(x,a) & = & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)(j+\frac{1}{2})}{N}}\nonumber\\ \displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}(\text{exp}(2A_{N,j+\frac{1}{2}}(\frac{n}{x}))-1)}.\end{eqnarray}$$ In fact, the above expressions for ![]() $J_{1}(x,a)$ differ from the expression in the first equality in [Reference Kanemitsu, Tanigawa and Yoshimoto35, Equation (2.18)] only in that the numerator of the summand of the infinite series in them involves
$J_{1}(x,a)$ differ from the expression in the first equality in [Reference Kanemitsu, Tanigawa and Yoshimoto35, Equation (2.18)] only in that the numerator of the summand of the infinite series in them involves ![]() $\cos (2\unicode[STIX]{x1D70B}na)$, which is absent in the latter.
$\cos (2\unicode[STIX]{x1D70B}na)$, which is absent in the latter.
Finally, adding the corresponding sides of (4.27) and (4.24) when ![]() $N$ is odd, and respectively of (4.28) and (4.26) when
$N$ is odd, and respectively of (4.28) and (4.26) when ![]() $N$ is even gives expressions for
$N$ is even gives expressions for ![]() $J(x,a)$ (see (4.15)). These are nothing but the expressions for
$J(x,a)$ (see (4.15)). These are nothing but the expressions for ![]() $S(x,a)$ claimed in the statement of Theorem 2.1. Along with (4.11), this completes the proof of Theorem 2.1.◻
$S(x,a)$ claimed in the statement of Theorem 2.1. Along with (4.11), this completes the proof of Theorem 2.1.◻
As remarked in the Introduction, a special case of the above result for ![]() $N$ even was previously obtained by Kanemitsu, Tanigawa and Yoshimoto [Reference Kanemitsu, Tanigawa and Yoshimoto37, Theorem 2.1]. Before deriving their result from ours, we begin with [Reference Dixit and Maji21, Lemma 3.1].
$N$ even was previously obtained by Kanemitsu, Tanigawa and Yoshimoto [Reference Kanemitsu, Tanigawa and Yoshimoto37, Theorem 2.1]. Before deriving their result from ours, we begin with [Reference Dixit and Maji21, Lemma 3.1].
Lemma 4.4. For ![]() $a,u,v\in \mathbb{R}$, we have
$a,u,v\in \mathbb{R}$, we have
Theorem 4.5. Kanemitsu et al. [Reference Kanemitsu, Tanigawa and Yoshimoto37]
Let ![]() $h^{\prime }\geqslant 0$,
$h^{\prime }\geqslant 0$, ![]() $\ell \geqslant 0$ and
$\ell \geqslant 0$ and ![]() $M\geqslant 1$ be fixed integers with
$M\geqslant 1$ be fixed integers with ![]() $h^{\prime }<M$, and let
$h^{\prime }<M$, and let ![]() $0<a\leqslant 1$. Let
$0<a\leqslant 1$. Let ![]() $x>0$,
$x>0$, ![]() $A(y)=\unicode[STIX]{x1D70B}(2\unicode[STIX]{x1D70B}y)^{\frac{1}{2M}}$ and let
$A(y)=\unicode[STIX]{x1D70B}(2\unicode[STIX]{x1D70B}y)^{\frac{1}{2M}}$ and let
 $$\begin{eqnarray}\displaystyle a_{j} & := & \displaystyle \cos \biggl(\frac{\unicode[STIX]{x1D70B}}{2M}\biggl(\frac{1}{2}-j\biggr)\biggr),\qquad b_{j}:=\sin \biggl(\frac{\unicode[STIX]{x1D70B}}{2M}\biggl(\frac{1}{2}-j\biggr)\biggr),\nonumber\\ \displaystyle B_{j}(n,h^{\prime },\ell ) & := & \displaystyle -2\unicode[STIX]{x1D70B}an-\frac{\unicode[STIX]{x1D70B}(2h^{\prime }+1)}{2M}\biggl(\frac{1}{2}-j\biggr)-\frac{\unicode[STIX]{x1D70B}(\ell -1)}{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{j} & := & \displaystyle \cos \biggl(\frac{\unicode[STIX]{x1D70B}}{2M}\biggl(\frac{1}{2}-j\biggr)\biggr),\qquad b_{j}:=\sin \biggl(\frac{\unicode[STIX]{x1D70B}}{2M}\biggl(\frac{1}{2}-j\biggr)\biggr),\nonumber\\ \displaystyle B_{j}(n,h^{\prime },\ell ) & := & \displaystyle -2\unicode[STIX]{x1D70B}an-\frac{\unicode[STIX]{x1D70B}(2h^{\prime }+1)}{2M}\biggl(\frac{1}{2}-j\biggr)-\frac{\unicode[STIX]{x1D70B}(\ell -1)}{2},\nonumber\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & & \displaystyle f_{j}(n,h^{\prime },\ell ,x)\nonumber\\ \displaystyle & & \displaystyle \quad :=\frac{\cos (2A(\frac{n}{x})b_{j}+B_{j}(n,h^{\prime },\ell ))-e^{-2A(\frac{n}{x})a_{j}}\cos (B_{j}(n,h^{\prime },\ell ))}{\cosh (2A(\frac{n}{x})a_{j})-\cos (2A(\frac{n}{x})b_{j})}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f_{j}(n,h^{\prime },\ell ,x)\nonumber\\ \displaystyle & & \displaystyle \quad :=\frac{\cos (2A(\frac{n}{x})b_{j}+B_{j}(n,h^{\prime },\ell ))-e^{-2A(\frac{n}{x})a_{j}}\cos (B_{j}(n,h^{\prime },\ell ))}{\cosh (2A(\frac{n}{x})a_{j})-\cos (2A(\frac{n}{x})b_{j})}.\end{eqnarray}$$Let
 $$\begin{eqnarray}\displaystyle P(x) & := & \displaystyle \unicode[STIX]{x1D701}(2M(\ell +1)-2h^{\prime })x^{-1}+\mathop{\sum }_{j=0}^{\ell }\frac{(-1)^{j}}{j!}\unicode[STIX]{x1D701}(-j,a)\unicode[STIX]{x1D701}(2M(\ell -j)-2h^{\prime })x^{j}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2M}\unicode[STIX]{x1D6E4}\biggl(-\ell +\frac{2h^{\prime }+1}{2M}\biggr)\unicode[STIX]{x1D701}\biggl(-\ell +\frac{2h^{\prime }+1}{2M},a\biggr)x^{\ell -\frac{2h^{\prime }+1}{2M}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(x) & := & \displaystyle \unicode[STIX]{x1D701}(2M(\ell +1)-2h^{\prime })x^{-1}+\mathop{\sum }_{j=0}^{\ell }\frac{(-1)^{j}}{j!}\unicode[STIX]{x1D701}(-j,a)\unicode[STIX]{x1D701}(2M(\ell -j)-2h^{\prime })x^{j}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2M}\unicode[STIX]{x1D6E4}\biggl(-\ell +\frac{2h^{\prime }+1}{2M}\biggr)\unicode[STIX]{x1D701}\biggl(-\ell +\frac{2h^{\prime }+1}{2M},a\biggr)x^{\ell -\frac{2h^{\prime }+1}{2M}}.\end{eqnarray}$$Then,
where, for ![]() $M$ even,
$M$ even,
 $$\begin{eqnarray}\displaystyle U(x,a) & := & \displaystyle \frac{(-1)^{h^{\prime }}}{2M}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{2M}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{M}{2}}^{\frac{M}{2}-1}\mathop{\sum }_{n=1}^{\infty }f_{2j+1}(n,h^{\prime },\ell ,x)n^{-1-\ell +\frac{2h^{\prime }+1}{2M}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U(x,a) & := & \displaystyle \frac{(-1)^{h^{\prime }}}{2M}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{2M}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-\frac{M}{2}}^{\frac{M}{2}-1}\mathop{\sum }_{n=1}^{\infty }f_{2j+1}(n,h^{\prime },\ell ,x)n^{-1-\ell +\frac{2h^{\prime }+1}{2M}},\end{eqnarray}$$ and for ![]() $M$ odd,
$M$ odd,
 $$\begin{eqnarray}U(x,a):=\frac{(-1)^{h^{\prime }}}{2M}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{2M}}\mathop{\sum }_{j=-\frac{M-1}{2}}^{\frac{M-1}{2}}\mathop{\sum }_{n=1}^{\infty }f_{2j}(n,h^{\prime },\ell ,x)n^{-1-\ell +\frac{2h^{\prime }+1}{2M}}.\end{eqnarray}$$
$$\begin{eqnarray}U(x,a):=\frac{(-1)^{h^{\prime }}}{2M}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{2M}}\mathop{\sum }_{j=-\frac{M-1}{2}}^{\frac{M-1}{2}}\mathop{\sum }_{n=1}^{\infty }f_{2j}(n,h^{\prime },\ell ,x)n^{-1-\ell +\frac{2h^{\prime }+1}{2M}}.\end{eqnarray}$$Proof. Substitute ![]() $N=2M$ and
$N=2M$ and ![]() $h=M-h^{\prime }+M\ell$ on both sides of (2.1). Then the resulting left-hand side is the same as the Lambert series in (4.31). With the above substitutions,
$h=M-h^{\prime }+M\ell$ on both sides of (2.1). Then the resulting left-hand side is the same as the Lambert series in (4.31). With the above substitutions,
 $$\begin{eqnarray}\displaystyle P(x,a) & = & \displaystyle \frac{1}{2M}\unicode[STIX]{x1D6E4}\biggl(-\ell +\frac{2h^{\prime }+1}{2M}\biggr)\unicode[STIX]{x1D701}\biggl(-\ell +\frac{2h^{\prime }+1}{2M},a\biggr)x^{\ell -\frac{2h^{\prime }+1}{2M}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{j=0}^{\lfloor \frac{\ell }{2}-\frac{h^{\prime }}{2M}\rfloor }\frac{\unicode[STIX]{x1D701}(-2j,a)}{(2j)!}\unicode[STIX]{x1D701}(2M(\ell -2j)-2h^{\prime })x^{2j}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D701}(2M(\ell +1)-2h^{\prime })}{x}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{j=1}^{\lfloor \frac{\ell }{2}-\frac{h^{\prime }}{2M}+\frac{1}{2}\rfloor }\frac{(-1)^{2j-1}}{(2j-1)!}\frac{\unicode[STIX]{x1D701}(-(2j-1),a)}{x^{1-2j}}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(-4Mj+2M-2h^{\prime }+2M\ell ).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(x,a) & = & \displaystyle \frac{1}{2M}\unicode[STIX]{x1D6E4}\biggl(-\ell +\frac{2h^{\prime }+1}{2M}\biggr)\unicode[STIX]{x1D701}\biggl(-\ell +\frac{2h^{\prime }+1}{2M},a\biggr)x^{\ell -\frac{2h^{\prime }+1}{2M}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{j=0}^{\lfloor \frac{\ell }{2}-\frac{h^{\prime }}{2M}\rfloor }\frac{\unicode[STIX]{x1D701}(-2j,a)}{(2j)!}\unicode[STIX]{x1D701}(2M(\ell -2j)-2h^{\prime })x^{2j}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D701}(2M(\ell +1)-2h^{\prime })}{x}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{j=1}^{\lfloor \frac{\ell }{2}-\frac{h^{\prime }}{2M}+\frac{1}{2}\rfloor }\frac{(-1)^{2j-1}}{(2j-1)!}\frac{\unicode[STIX]{x1D701}(-(2j-1),a)}{x^{1-2j}}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(-4Mj+2M-2h^{\prime }+2M\ell ).\end{eqnarray}$$ Note that ![]() $0<h^{\prime }<M\Rightarrow 0<\frac{1}{2}-\frac{h^{\prime }}{2m}<\frac{1}{2}\Rightarrow \lfloor \frac{1}{2}-\frac{h^{\prime }}{2m}\rfloor =0$, and
$0<h^{\prime }<M\Rightarrow 0<\frac{1}{2}-\frac{h^{\prime }}{2m}<\frac{1}{2}\Rightarrow \lfloor \frac{1}{2}-\frac{h^{\prime }}{2m}\rfloor =0$, and ![]() $0<h^{\prime }<M\Rightarrow -\frac{1}{2}<-\frac{h^{\prime }}{2M}<0\Rightarrow \lfloor -\frac{h^{\prime }}{2M}\rfloor =-1$. Thus,
$0<h^{\prime }<M\Rightarrow -\frac{1}{2}<-\frac{h^{\prime }}{2M}<0\Rightarrow \lfloor -\frac{h^{\prime }}{2M}\rfloor =-1$. Thus,
 $$\begin{eqnarray}\displaystyle \biggl\lfloor\frac{\ell }{2}+\frac{1}{2}-\frac{h^{\prime }}{2m}\biggr\rfloor & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\ell }{2}\quad & \ell \text{ is even},\\ \displaystyle \frac{\ell -1}{2}\quad & \ell \text{ is odd},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl\lfloor\frac{\ell }{2}+\frac{1}{2}-\frac{h^{\prime }}{2m}\biggr\rfloor & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\ell }{2}\quad & \ell \text{ is even},\\ \displaystyle \frac{\ell -1}{2}\quad & \ell \text{ is odd},\end{array}\right.\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle \biggl\lfloor\frac{\ell }{2}-\frac{h^{\prime }}{2M}\biggr\rfloor & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\ell }{2}-1\quad & \ell \text{ is even},\\ \displaystyle \frac{\ell -1}{2}\quad & \ell \text{ is odd}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl\lfloor\frac{\ell }{2}-\frac{h^{\prime }}{2M}\biggr\rfloor & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\ell }{2}-1\quad & \ell \text{ is even},\\ \displaystyle \frac{\ell -1}{2}\quad & \ell \text{ is odd}.\end{array}\right.\end{eqnarray}$$ Using (4.35) and (4.36), we see that, irrespective of the parity of ![]() $\ell$, the two finite sums over
$\ell$, the two finite sums over ![]() $j$ in (4.34) combine together to give
$j$ in (4.34) combine together to give
which, when combined with the other expression in (4.34), shows that our ![]() $P(x,a)$ equals
$P(x,a)$ equals ![]() $P(x)$, which is defined in (4.30).
$P(x)$, which is defined in (4.30).
Next, we have to show that our ![]() $S(x,a)$ from (2.4) matches with the expressions for
$S(x,a)$ from (2.4) matches with the expressions for ![]() $U(x,a)$ in (4.32) and (4.33) corresponding to
$U(x,a)$ in (4.32) and (4.33) corresponding to ![]() $M$ even and
$M$ even and ![]() $M$ odd, respectively. We only prove this in the case when
$M$ odd, respectively. We only prove this in the case when ![]() $M$ is even. That for
$M$ is even. That for ![]() $M$ odd can be similarly proved.
$M$ odd can be similarly proved.
Substitute ![]() $N=2M$,
$N=2M$, ![]() $h=M-h^{\prime }+M\ell$, with
$h=M-h^{\prime }+M\ell$, with ![]() $M$ even, say
$M$ even, say ![]() $M=2k$, in (2.4) and simplify to get
$M=2k$, in (2.4) and simplify to get
 $$\begin{eqnarray}\displaystyle S(x,a) & = & \displaystyle \frac{(-1)^{h^{\prime }+1}}{4k}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{4k}}\mathop{\sum }_{n=1}^{\infty }n^{-1-\ell +\frac{1+2h^{\prime }}{4k}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-2k}^{2k-1}\exp \biggl(\frac{i\unicode[STIX]{x1D70B}(1-4k+2h^{\prime }-4k\ell )(j+\frac{1}{2})}{4k}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{(\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+1}\sin (2\unicode[STIX]{x1D70B}na))}{\exp (2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{4k}}e^{\frac{i\unicode[STIX]{x1D70B}}{4k}(j+\frac{1}{2})})-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(x,a) & = & \displaystyle \frac{(-1)^{h^{\prime }+1}}{4k}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{4k}}\mathop{\sum }_{n=1}^{\infty }n^{-1-\ell +\frac{1+2h^{\prime }}{4k}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{j=-2k}^{2k-1}\exp \biggl(\frac{i\unicode[STIX]{x1D70B}(1-4k+2h^{\prime }-4k\ell )(j+\frac{1}{2})}{4k}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{(\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+1}\sin (2\unicode[STIX]{x1D70B}na))}{\exp (2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{4k}}e^{\frac{i\unicode[STIX]{x1D70B}}{4k}(j+\frac{1}{2})})-1}.\nonumber\end{eqnarray}$$ Now split the sum over ![]() $j$ according to the parity of
$j$ according to the parity of ![]() $j$ and simplify so as to obtain
$j$ and simplify so as to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle S(x,a)=\frac{(-1)^{h^{\prime }+1}}{4k}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{4k}}\mathop{\sum }_{n=1}^{\infty }n^{-1-\ell +\frac{1+2h^{\prime }}{4k}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\bigg\{\mathop{\sum }_{j=-k}^{k-1}\frac{\exp (-i(2\unicode[STIX]{x1D70B}na-\frac{\unicode[STIX]{x1D70B}(2h^{\prime }+1)}{4k}(\frac{4j+1}{2})+\frac{(\ell +1)}{2}(4j+1)\unicode[STIX]{x1D70B}))}{\exp (2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{4k}}e^{\frac{i\unicode[STIX]{x1D70B}}{4k}(\frac{4j+1}{2})})-1}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{j=-k}^{k-1}\frac{\exp (i(2\unicode[STIX]{x1D70B}na+\frac{\unicode[STIX]{x1D70B}(2h^{\prime }+1)}{4k}(\frac{4j+3}{2})-\frac{(\ell +1)}{2}(4j+3)\unicode[STIX]{x1D70B}))}{\exp (2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{4k}}e^{\frac{i\unicode[STIX]{x1D70B}}{4k}(\frac{4j+3}{2})})-1}\bigg\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle S(x,a)=\frac{(-1)^{h^{\prime }+1}}{4k}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{4k}}\mathop{\sum }_{n=1}^{\infty }n^{-1-\ell +\frac{1+2h^{\prime }}{4k}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\bigg\{\mathop{\sum }_{j=-k}^{k-1}\frac{\exp (-i(2\unicode[STIX]{x1D70B}na-\frac{\unicode[STIX]{x1D70B}(2h^{\prime }+1)}{4k}(\frac{4j+1}{2})+\frac{(\ell +1)}{2}(4j+1)\unicode[STIX]{x1D70B}))}{\exp (2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{4k}}e^{\frac{i\unicode[STIX]{x1D70B}}{4k}(\frac{4j+1}{2})})-1}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{j=-k}^{k-1}\frac{\exp (i(2\unicode[STIX]{x1D70B}na+\frac{\unicode[STIX]{x1D70B}(2h^{\prime }+1)}{4k}(\frac{4j+3}{2})-\frac{(\ell +1)}{2}(4j+3)\unicode[STIX]{x1D70B}))}{\exp (2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{4k}}e^{\frac{i\unicode[STIX]{x1D70B}}{4k}(\frac{4j+3}{2})})-1}\bigg\}.\nonumber\end{eqnarray}$$ Replace ![]() $j$ by
$j$ by ![]() $-j-1$ in the second sum and then observe that the resulting corresponding summands of the two sums are complex conjugates of each other so that
$-j-1$ in the second sum and then observe that the resulting corresponding summands of the two sums are complex conjugates of each other so that
 $$\begin{eqnarray}\displaystyle S(x,a) & = & \displaystyle \frac{(-1)^{h^{\prime }+1}}{4k}\biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)^{\ell -\frac{(2h^{\prime }+1)}{4k}}\mathop{\sum }_{n=1}^{\infty }n^{-1-\ell +\frac{1+2h^{\prime }}{4k}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{j=-k}^{k-1}2\text{Re}\biggl(\frac{e^{iuv}}{\exp (ae^{-iu})-1}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(x,a) & = & \displaystyle \frac{(-1)^{h^{\prime }+1}}{4k}\biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)^{\ell -\frac{(2h^{\prime }+1)}{4k}}\mathop{\sum }_{n=1}^{\infty }n^{-1-\ell +\frac{1+2h^{\prime }}{4k}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{j=-k}^{k-1}2\text{Re}\biggl(\frac{e^{iuv}}{\exp (ae^{-iu})-1}\biggr),\nonumber\end{eqnarray}$$ where ![]() $a=2A(\frac{n}{x}),u=-\frac{\unicode[STIX]{x1D70B}}{4k}(\frac{4j+1}{2})$, and
$a=2A(\frac{n}{x}),u=-\frac{\unicode[STIX]{x1D70B}}{4k}(\frac{4j+1}{2})$, and ![]() $uv=-2\unicode[STIX]{x1D70B}an+\frac{\unicode[STIX]{x1D70B}(2h^{\prime }+1)}{4k}(\frac{4j+1}{2})-\frac{\unicode[STIX]{x1D70B}(\ell +1)(4j+1)}{2}$. Using Lemma 4.4, the hypotheses of Theorem 4.5, (4.29) and the fact that
$uv=-2\unicode[STIX]{x1D70B}an+\frac{\unicode[STIX]{x1D70B}(2h^{\prime }+1)}{4k}(\frac{4j+1}{2})-\frac{\unicode[STIX]{x1D70B}(\ell +1)(4j+1)}{2}$. Using Lemma 4.4, the hypotheses of Theorem 4.5, (4.29) and the fact that ![]() $k=M/2$, we deduce that
$k=M/2$, we deduce that
 $$\begin{eqnarray}S(x,a)=\frac{(-1)^{h^{\prime }}}{4k}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{4k}}\mathop{\sum }_{j=-\frac{M}{2}}^{\frac{M}{2}-1}\mathop{\sum }_{n=1}^{\infty }f_{2j+1}(n,h^{\prime },\ell ,x)n^{-1-\ell +\frac{1+2h^{\prime }}{4k}},\end{eqnarray}$$
$$\begin{eqnarray}S(x,a)=\frac{(-1)^{h^{\prime }}}{4k}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{-\ell +\frac{2h^{\prime }+1}{4k}}\mathop{\sum }_{j=-\frac{M}{2}}^{\frac{M}{2}-1}\mathop{\sum }_{n=1}^{\infty }f_{2j+1}(n,h^{\prime },\ell ,x)n^{-1-\ell +\frac{1+2h^{\prime }}{4k}},\end{eqnarray}$$which is nothing but (4.32). Thus we derive (4.31) from (2.1). As remarked before, (4.33) can be proved by a similar argument.◻
5 A two-parameter generalization of Ramanujan’s formula for  $\unicode[STIX]{x1D701}(2m+1)$
$\unicode[STIX]{x1D701}(2m+1)$
This section is devoted to proving Theorems 2.3 and 2.4, which, as will be seen, are equivalent to each other. We then give interesting special cases of Theorem 2.4. We begin with a lemma.
Lemma 5.1. Let ![]() $N$ be an odd positive integer. If
$N$ be an odd positive integer. If ![]() $h>\frac{N}{2}$, then
$h>\frac{N}{2}$, then ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ if and only if
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ if and only if ![]() $h=\frac{N+1}{2}+Nm$, where
$h=\frac{N+1}{2}+Nm$, where ![]() $m\in \mathbb{N}\cup \{0\}$.
$m\in \mathbb{N}\cup \{0\}$.
Proof. Let ![]() $\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =m$. Since
$\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =m$. Since ![]() $h>N/2$, we have
$h>N/2$, we have ![]() $m\in \mathbb{N}\cup \{0\}$. Let
$m\in \mathbb{N}\cup \{0\}$. Let ![]() $\frac{h}{N}-\frac{1}{2}=m+r$, where
$\frac{h}{N}-\frac{1}{2}=m+r$, where ![]() $0\leqslant r<1$. Then
$0\leqslant r<1$. Then ![]() $h=\frac{N}{2}+N(m+r)$. From the hypothesis,
$h=\frac{N}{2}+N(m+r)$. From the hypothesis, ![]() $N-2h+1=-2Nm$. Since the last two equations imply
$N-2h+1=-2Nm$. Since the last two equations imply ![]() $r=\frac{1}{2N}$, we get
$r=\frac{1}{2N}$, we get ![]() $h=\frac{N+1}{2}+Nm$. The other direction is trivial.◻
$h=\frac{N+1}{2}+Nm$. The other direction is trivial.◻
Proof of Theorem 2.3.
The setup for the proof of this theorem is exactly similar to that of Theorem 2.1. Hence we only give details where they differ from those of the latter.
Note that ![]() $a\in (0,1]$ is fixed, and our integrand
$a\in (0,1]$ is fixed, and our integrand ![]() $F(s)$, defined in (4.5), is
$F(s)$, defined in (4.5), is ![]() $F(s):=\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))x^{-s}$. The poles of
$F(s):=\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))x^{-s}$. The poles of ![]() $\unicode[STIX]{x1D6E4}(s)$ include negative even integers, whereas
$\unicode[STIX]{x1D6E4}(s)$ include negative even integers, whereas ![]() $\unicode[STIX]{x1D701}(Ns-(N-2h))$ has a simple pole at
$\unicode[STIX]{x1D701}(Ns-(N-2h))$ has a simple pole at ![]() $s=\frac{N-2h+1}{N}$. Since
$s=\frac{N-2h+1}{N}$. Since ![]() $N$ is odd, it may happen that
$N$ is odd, it may happen that ![]() $\frac{N-2h+1}{N}=-2j$ for some positive integers
$\frac{N-2h+1}{N}=-2j$ for some positive integers ![]() $N$ and
$N$ and ![]() $j$. As explained in the Introduction, Lemma 4.2 then implies that
$j$. As explained in the Introduction, Lemma 4.2 then implies that ![]() $j=\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$. This may imply a double order pole of
$j=\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$. This may imply a double order pole of ![]() $F(s)$ at
$F(s)$ at ![]() $s=\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ if
$s=\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ if ![]() $\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)\neq 0$, or a simple pole (or a removable singularity) if
$\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)\neq 0$, or a simple pole (or a removable singularity) if ![]() $\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)=0$. However, even if
$\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)=0$. However, even if ![]() $\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)=0$, one may first calculate the residue assuming a double pole and then apply this fact, and the answer obtained would be same as that deduced by first applying
$\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)=0$, one may first calculate the residue assuming a double pole and then apply this fact, and the answer obtained would be same as that deduced by first applying ![]() $\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)=0$ and then accordingly calculating the residue.
$\unicode[STIX]{x1D701}(\frac{N-2h+1}{N},a)=0$ and then accordingly calculating the residue.
Thus the residue at ![]() $\frac{N-2h+1}{N}$ is given by
$\frac{N-2h+1}{N}$ is given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle R_{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{s\rightarrow \frac{N-2h+1}{N}}\biggl(\frac{\text{d}}{\text{d}s}\biggl(s-\frac{N-2h+1}{N}\biggr)^{2}\frac{\unicode[STIX]{x1D6E4}(s)}{x^{s}}\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x^{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }}{N(2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor )!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{-\frac{B_{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}(a)}{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}\biggl(\unicode[STIX]{x1D713}\biggl(2\biggl\lfloor\frac{h}{N}-\frac{1}{2}\biggr\rfloor+1\biggr)+N\unicode[STIX]{x1D6FE}-\log x\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D701}^{\prime }\biggl(-2\biggl\lfloor\frac{h}{N}-\frac{1}{2}\biggr\rfloor,a\biggr)\bigg\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle R_{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{s\rightarrow \frac{N-2h+1}{N}}\biggl(\frac{\text{d}}{\text{d}s}\biggl(s-\frac{N-2h+1}{N}\biggr)^{2}\frac{\unicode[STIX]{x1D6E4}(s)}{x^{s}}\unicode[STIX]{x1D701}(s,a)\unicode[STIX]{x1D701}(Ns-(N-2h))\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x^{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }}{N(2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor )!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{-\frac{B_{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}(a)}{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}\biggl(\unicode[STIX]{x1D713}\biggl(2\biggl\lfloor\frac{h}{N}-\frac{1}{2}\biggr\rfloor+1\biggr)+N\unicode[STIX]{x1D6FE}-\log x\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D701}^{\prime }\biggl(-2\biggl\lfloor\frac{h}{N}-\frac{1}{2}\biggr\rfloor,a\biggr)\bigg\}.\end{eqnarray}$$Thus, from (4.6), (4.7), (4.9), (4.10), (5.1) and (2.3), we see that
where
 $$\begin{eqnarray}\displaystyle P^{\ast }(x,a) & := & \displaystyle -\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h)+\frac{\unicode[STIX]{x1D701}(2h)}{x}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor -1}\frac{B_{2j+1}(a)}{(2j+1)!}\frac{\unicode[STIX]{x1D701}(2h-(2j+1)N)}{x^{-2j}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{x^{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }}{N(2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor )!}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg\{\frac{-B_{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}(a)}{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}\biggl(\unicode[STIX]{x1D713}\biggl(2\biggl\lfloor\frac{h}{N}-\frac{1}{2}\biggr\rfloor+1\biggr)+N\unicode[STIX]{x1D6FE}-\log x\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D701}^{\prime }\biggl(-2\biggl\lfloor\frac{h}{N}-\frac{1}{2}\biggr\rfloor,a\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{h+1}2^{2h-1}\unicode[STIX]{x1D70B}^{2h}\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{2h-2jN}}{(2j)!(2h-2jN)!}x^{2j-1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P^{\ast }(x,a) & := & \displaystyle -\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h)+\frac{\unicode[STIX]{x1D701}(2h)}{x}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}-\frac{1}{2}\rfloor -1}\frac{B_{2j+1}(a)}{(2j+1)!}\frac{\unicode[STIX]{x1D701}(2h-(2j+1)N)}{x^{-2j}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{x^{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor }}{N(2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor )!}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg\{\frac{-B_{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}(a)}{2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor +1}\biggl(\unicode[STIX]{x1D713}\biggl(2\biggl\lfloor\frac{h}{N}-\frac{1}{2}\biggr\rfloor+1\biggr)+N\unicode[STIX]{x1D6FE}-\log x\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D701}^{\prime }\biggl(-2\biggl\lfloor\frac{h}{N}-\frac{1}{2}\biggr\rfloor,a\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{h+1}2^{2h-1}\unicode[STIX]{x1D70B}^{2h}\mathop{\sum }_{j=1}^{\lfloor \frac{h}{N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{2h-2jN}}{(2j)!(2h-2jN)!}x^{2j-1},\end{eqnarray}$$ and the calculation for ![]() $S(x,a)$ remains exactly the same as in the proof of Theorem 2.1.
$S(x,a)$ remains exactly the same as in the proof of Theorem 2.1.
As we now show, (5.2) can be simplified to a great extent using the following result of Koyama and Kurokawa [Reference Koyama and Kurokawa39, page 7] for an even positive integer ![]() $k$ and
$k$ and ![]() $0<a\leqslant 1$:
$0<a\leqslant 1$:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}^{\prime }(-k,a) & = & \displaystyle \frac{2(-1)^{\frac{k}{2}}k!}{(2\unicode[STIX]{x1D70B})^{k+1}}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{(\log n)\sin (2\unicode[STIX]{x1D70B}na)}{n^{k+1}}\nonumber\\ \displaystyle & & \displaystyle +\,(\log (2\unicode[STIX]{x1D70B})-\unicode[STIX]{x1D713}(k+1))\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{k+1}}+\frac{\unicode[STIX]{x1D70B}}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{k+1}}\bigg\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}^{\prime }(-k,a) & = & \displaystyle \frac{2(-1)^{\frac{k}{2}}k!}{(2\unicode[STIX]{x1D70B})^{k+1}}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{(\log n)\sin (2\unicode[STIX]{x1D70B}na)}{n^{k+1}}\nonumber\\ \displaystyle & & \displaystyle +\,(\log (2\unicode[STIX]{x1D70B})-\unicode[STIX]{x1D713}(k+1))\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{k+1}}+\frac{\unicode[STIX]{x1D70B}}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{k+1}}\bigg\}.\end{eqnarray}$$ Though Koyama and Kurokawa write ![]() $\log (2\unicode[STIX]{x1D70B})+\unicode[STIX]{x1D6FE}-\sum _{i=1}^{k}\frac{1}{i}$ in place of
$\log (2\unicode[STIX]{x1D70B})+\unicode[STIX]{x1D6FE}-\sum _{i=1}^{k}\frac{1}{i}$ in place of ![]() $(\log (2\unicode[STIX]{x1D70B})-\unicode[STIX]{x1D713}(k+1))$, using the functional equation
$(\log (2\unicode[STIX]{x1D70B})-\unicode[STIX]{x1D713}(k+1))$, using the functional equation ![]() $\unicode[STIX]{x1D713}(z+1)=\unicode[STIX]{x1D713}(z)+\frac{1}{z}$, it is seen that they are equal. Also, even though they work with
$\unicode[STIX]{x1D713}(z+1)=\unicode[STIX]{x1D713}(z)+\frac{1}{z}$, it is seen that they are equal. Also, even though they work with ![]() $0<a<1$, the formula holds for
$0<a<1$, the formula holds for ![]() $a=1$ as long as
$a=1$ as long as ![]() $k$ is even,
$k$ is even, ![]() $k>0$, and is then a well-known result
$k>0$, and is then a well-known result ![]() $\unicode[STIX]{x1D701}^{\prime }(-k)=\frac{1}{2}(-1)^{\frac{k}{2}}(2\unicode[STIX]{x1D70B})^{-k}(k!)\unicode[STIX]{x1D701}(k+1)$ [Reference Kanemitsu, Tanigawa and Yoshimoto36, Equation (1)].
$\unicode[STIX]{x1D701}^{\prime }(-k)=\frac{1}{2}(-1)^{\frac{k}{2}}(2\unicode[STIX]{x1D70B})^{-k}(k!)\unicode[STIX]{x1D701}(k+1)$ [Reference Kanemitsu, Tanigawa and Yoshimoto36, Equation (1)].
It is important to note that (5.4) also holds for ![]() $k=0$ but only for
$k=0$ but only for ![]() $0<a<1$, and is then an equivalent form of the well-known Kummer formula for
$0<a<1$, and is then an equivalent form of the well-known Kummer formula for ![]() $\log \unicode[STIX]{x1D6E4}(a)$ [Reference Kummer40, page 4].
$\log \unicode[STIX]{x1D6E4}(a)$ [Reference Kummer40, page 4].
By Lemma 5.1, we know that for ![]() $h>N/2$, we have
$h>N/2$, we have ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ if and only if
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor$ if and only if ![]() $h=\frac{N+1}{2}+Nm$, where
$h=\frac{N+1}{2}+Nm$, where ![]() $m\in \mathbb{N}$. Thus, we let
$m\in \mathbb{N}$. Thus, we let ![]() $h=\frac{N+1}{2}+Nm$ in (5.2), employ (5.4) with
$h=\frac{N+1}{2}+Nm$ in (5.2), employ (5.4) with ![]() $k=2m$ in the expression for the residue in (5.3) arising due to double pole to simplify it as
$k=2m$ in the expression for the residue in (5.3) arising due to double pole to simplify it as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{x^{2m}}{N(2m)!}\bigg\{-\frac{B_{2m+1}(a)}{2m+1}(\unicode[STIX]{x1D713}(2m+1)+N\unicode[STIX]{x1D6FE}-\log x)+\unicode[STIX]{x1D701}^{\prime }(-2m,a)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x^{2m}B_{2m+1}(a)}{N(2m+1)!}\biggl(-N\unicode[STIX]{x1D6FE}+\log \biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{2(-1)^{m}x^{2m}}{N(2\unicode[STIX]{x1D70B})^{2m+1}}\biggl(\mathop{\sum }_{n=1}^{\infty }\frac{(\log n)\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}+\frac{\unicode[STIX]{x1D70B}}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{x^{2m}}{N(2m)!}\bigg\{-\frac{B_{2m+1}(a)}{2m+1}(\unicode[STIX]{x1D713}(2m+1)+N\unicode[STIX]{x1D6FE}-\log x)+\unicode[STIX]{x1D701}^{\prime }(-2m,a)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x^{2m}B_{2m+1}(a)}{N(2m+1)!}\biggl(-N\unicode[STIX]{x1D6FE}+\log \biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{2(-1)^{m}x^{2m}}{N(2\unicode[STIX]{x1D70B})^{2m+1}}\biggl(\mathop{\sum }_{n=1}^{\infty }\frac{(\log n)\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}+\frac{\unicode[STIX]{x1D70B}}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\biggr),\end{eqnarray}$$ where, in the course of simplification, the series ![]() $\sum _{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}$ is expressed in terms of Bernoulli polynomials using their Fourier expansion [Reference Abramowitz and Stegun1, page 805]:
$\sum _{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}$ is expressed in terms of Bernoulli polynomials using their Fourier expansion [Reference Abramowitz and Stegun1, page 805]:
Moreover, part of the expression for ![]() $S(x,a)$ in (2.3) can be simplified:
$S(x,a)$ in (2.3) can be simplified:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}\text{exp}\biggl(\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}\biggr)\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-1)^{m+\frac{N+3}{2}}}{N}\biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)^{2m}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}\frac{(-1)^{2j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\log \biggl(\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-1)^{m+1}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)^{2m}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}\bigg\{\biggl(\frac{1}{N}\log \biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)+\frac{i\unicode[STIX]{x1D70B}j}{N}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{N}\mathop{\sum }_{n=1}^{\infty }\frac{(\log n)\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x^{2m}}{N(2m+1)!}\log \biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)B_{2m+1}(a)-\frac{(-1)^{m}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)^{2m}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{(\log n)\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}\text{exp}\biggl(\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}\biggr)\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-1)^{m+\frac{N+3}{2}}}{N}\biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)^{2m}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}\frac{(-1)^{2j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\log \biggl(\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-1)^{m+1}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)^{2m}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}\bigg\{\biggl(\frac{1}{N}\log \biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)+\frac{i\unicode[STIX]{x1D70B}j}{N}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{N}\mathop{\sum }_{n=1}^{\infty }\frac{(\log n)\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x^{2m}}{N(2m+1)!}\log \biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)B_{2m+1}(a)-\frac{(-1)^{m}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{x}{2\unicode[STIX]{x1D70B}}\biggr)^{2m}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{(\log n)\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}},\end{eqnarray}$$where in the last step, we again used (5.6). Now combine (5.5) and (5.7) to deduce that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{x^{2m}}{N(2m)!}\bigg\{-\frac{B_{2m+1}(a)}{2m+1}(\unicode[STIX]{x1D713}(2m+1)+N\unicode[STIX]{x1D6FE}-\log x)+\unicode[STIX]{x1D701}^{\prime }(-2m,a)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}\text{exp}\biggl(\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}\biggr)\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =-\unicode[STIX]{x1D6FE}B_{2m+1}(a)\frac{x^{2m}}{(2m+1)!}+\frac{(-1)^{m}x^{2m}\unicode[STIX]{x1D70B}}{N(2\unicode[STIX]{x1D70B})^{2m+1}}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{x^{2m}}{N(2m)!}\bigg\{-\frac{B_{2m+1}(a)}{2m+1}(\unicode[STIX]{x1D713}(2m+1)+N\unicode[STIX]{x1D6FE}-\log x)+\unicode[STIX]{x1D701}^{\prime }(-2m,a)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{h+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}\text{exp}\biggl(\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}\biggr)\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =-\unicode[STIX]{x1D6FE}B_{2m+1}(a)\frac{x^{2m}}{(2m+1)!}+\frac{(-1)^{m}x^{2m}\unicode[STIX]{x1D70B}}{N(2\unicode[STIX]{x1D70B})^{2m+1}}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}.\end{eqnarray}$$ Substituting (5.8) in (5.2) and noting that ![]() $m=\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =\frac{2h-1-N}{2N}$ leads us to (2.7).◻
$m=\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =\frac{2h-1-N}{2N}$ leads us to (2.7).◻
Proof of Theorem 2.4.
Let ![]() $h=\frac{N+1}{2}+Nm,m>0$,
$h=\frac{N+1}{2}+Nm,m>0$, ![]() $x=2^{N}\unicode[STIX]{x1D6FC}$ and
$x=2^{N}\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$ in Theorem 2.3. To write the sum over
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$ in Theorem 2.3. To write the sum over ![]() $j$ going from
$j$ going from ![]() $0$ to
$0$ to ![]() $\lfloor \frac{h}{N}\rfloor$ in terms of
$\lfloor \frac{h}{N}\rfloor$ in terms of ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FD}$, we use the fact that
$\unicode[STIX]{x1D6FD}$, we use the fact that
Now rearrange the terms of the resulting identity upon the aforementioned substitutions, multiply both sides of the rearranged identity by ![]() $\unicode[STIX]{x1D6FC}^{-2Nm/(N+1)}$, and then simplify to arrive at (2.8).◻
$\unicode[STIX]{x1D6FC}^{-2Nm/(N+1)}$, and then simplify to arrive at (2.8).◻
Letting ![]() $N=1$ in Theorem 2.4 gives the following result which can be thought of as a different one-parameter generalization, as compared to (1.2), of (1.1).
$N=1$ in Theorem 2.4 gives the following result which can be thought of as a different one-parameter generalization, as compared to (1.2), of (1.1).
Theorem 5.2. Let ![]() $0<a\leqslant 1$. Let
$0<a\leqslant 1$. Let ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$. Then for
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$. Then for ![]() $m\in \mathbb{Z},m>0$,
$m\in \mathbb{Z},m>0$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-m}\biggl(\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(2m+1)+\mathop{\sum }_{j=1}^{m-1}\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2m+1-2j)(2\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}\text{exp}(-2an\unicode[STIX]{x1D6FC})}{1-\text{exp}(-2n\unicode[STIX]{x1D6FC})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD})^{-m}\biggl[\frac{(-1)^{m+1}(2\unicode[STIX]{x1D70B})^{2m}B_{2m+1}(a)\unicode[STIX]{x1D6FE}}{(2m+1)!}+\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}\cos (2\unicode[STIX]{x1D70B}na)}{\text{exp}(2n\unicode[STIX]{x1D6FD})-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{in\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-in\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)\biggr)\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{m}2^{2m}\mathop{\sum }_{j=0}^{m+1}\frac{(-1)^{j}B_{2j}(a)B_{2m-2j+2}}{(2j)!(2m-2j+2)!}\unicode[STIX]{x1D6FC}^{j}\unicode[STIX]{x1D6FD}^{m+1-j}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-m}\biggl(\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(2m+1)+\mathop{\sum }_{j=1}^{m-1}\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2m+1-2j)(2\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}\text{exp}(-2an\unicode[STIX]{x1D6FC})}{1-\text{exp}(-2n\unicode[STIX]{x1D6FC})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =(-\unicode[STIX]{x1D6FD})^{-m}\biggl[\frac{(-1)^{m+1}(2\unicode[STIX]{x1D70B})^{2m}B_{2m+1}(a)\unicode[STIX]{x1D6FE}}{(2m+1)!}+\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2m-1}\cos (2\unicode[STIX]{x1D70B}na)}{\text{exp}(2n\unicode[STIX]{x1D6FD})-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1}}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{in\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-in\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}\biggr)\biggr)\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{m}2^{2m}\mathop{\sum }_{j=0}^{m+1}\frac{(-1)^{j}B_{2j}(a)B_{2m-2j+2}}{(2j)!(2m-2j+2)!}\unicode[STIX]{x1D6FC}^{j}\unicode[STIX]{x1D6FD}^{m+1-j}.\nonumber\end{eqnarray}$$ We now give corollaries of Theorem 2.4 when ![]() $a$ takes special values in the interval
$a$ takes special values in the interval ![]() $(0,1)$.
$(0,1)$.
5.1 A relation between  $\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ and
$\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ and  $\unicode[STIX]{x1D701}(11)$
$\unicode[STIX]{x1D701}(11)$
Proof of Corollary 2.5.
Let ![]() $E_{k}$ denote the
$E_{k}$ denote the ![]() $k$th Euler number, defined by
$k$th Euler number, defined by ![]() $\frac{1}{\cosh z}=\sum _{k=0}^{\infty }\frac{E_{k}}{k!}z^{k},|z|<\frac{1}{2}\unicode[STIX]{x1D70B}$. Let
$\frac{1}{\cosh z}=\sum _{k=0}^{\infty }\frac{E_{k}}{k!}z^{k},|z|<\frac{1}{2}\unicode[STIX]{x1D70B}$. Let ![]() $a=1/4$ in Theorem 2.4 to obtain
$a=1/4$ in Theorem 2.4 to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-\frac{2Nm}{N+1}}\biggl(-\frac{1}{4}\unicode[STIX]{x1D701}(2Nm+1)-\frac{1}{4}\mathop{\sum }_{j=1}^{m-1}\frac{E_{2j}}{(2j)!}\unicode[STIX]{x1D701}(2Nm+1-2jN)(2^{N-2}\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm-1}\text{exp}(-\frac{1}{4}(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-\unicode[STIX]{x1D6FD}^{\frac{2N}{N+1}})^{-m}2^{2m(N-1)}}{N}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl[\frac{(-1)^{m}\unicode[STIX]{x1D70B}^{2m}N\unicode[STIX]{x1D6FE}E_{2m}}{2^{2m+2}(2m)!}+\frac{(2^{-2m}-1)}{2^{2m+2}}\unicode[STIX]{x1D701}(2m+1)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\frac{1}{2^{2m+1}}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}n^{-2m-1}}{\text{exp}((4n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+3}{2}}}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (\frac{n\unicode[STIX]{x1D70B}}{2})}{n^{2m+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{m+\frac{N+3}{2}}2^{2Nm}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}+m\rfloor }\frac{(-1)^{j+1}2^{-2j}(1-2^{1-2j})B_{2j}B_{N+1+2N(m-j)}}{(2j)!(N+1+2N(m-j))!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)}{N+1}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}^{-\frac{2Nm}{N+1}}\biggl(-\frac{1}{4}\unicode[STIX]{x1D701}(2Nm+1)-\frac{1}{4}\mathop{\sum }_{j=1}^{m-1}\frac{E_{2j}}{(2j)!}\unicode[STIX]{x1D701}(2Nm+1-2jN)(2^{N-2}\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm-1}\text{exp}(-\frac{1}{4}(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\text{exp}(-(2n)^{N}\unicode[STIX]{x1D6FC})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-\unicode[STIX]{x1D6FD}^{\frac{2N}{N+1}})^{-m}2^{2m(N-1)}}{N}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl[\frac{(-1)^{m}\unicode[STIX]{x1D70B}^{2m}N\unicode[STIX]{x1D6FE}E_{2m}}{2^{2m+2}(2m)!}+\frac{(2^{-2m}-1)}{2^{2m+2}}\unicode[STIX]{x1D701}(2m+1)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}\mathop{\sum }_{j=\frac{-(N-1)}{2}}^{\frac{N-1}{2}}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\frac{1}{2^{2m+1}}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}n^{-2m-1}}{\text{exp}((4n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+3}{2}}}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (\frac{n\unicode[STIX]{x1D70B}}{2})}{n^{2m+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)+\unicode[STIX]{x1D713}\biggl(\frac{-i\unicode[STIX]{x1D6FD}}{2\unicode[STIX]{x1D70B}}(2n)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{m+\frac{N+3}{2}}2^{2Nm}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}+m\rfloor }\frac{(-1)^{j+1}2^{-2j}(1-2^{1-2j})B_{2j}B_{N+1+2N(m-j)}}{(2j)!(N+1+2N(m-j))!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FC}^{\frac{2j}{N+1}}\unicode[STIX]{x1D6FD}^{N+\frac{2N^{2}(m-j)}{N+1}},\nonumber\end{eqnarray}$$since [Reference Magnus, Oberhettinger and Soni46, page 26]
and ![]() $E_{2n+1}=0$. Now let
$E_{2n+1}=0$. Now let ![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}$,
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}$, ![]() $m=5$ and
$m=5$ and ![]() $N=1$ in the above identity and simplify.◻
$N=1$ in the above identity and simplify.◻
5.2 A new formula for  $\unicode[STIX]{x1D701}(2m+1)$
$\unicode[STIX]{x1D701}(2m+1)$
Proof of Theorem 2.6.
Let ![]() $a=1/2$ in Theorem 2.4. Use [Reference Temme61, page 4],
$a=1/2$ in Theorem 2.4. Use [Reference Temme61, page 4], ![]() $B_{j}(\frac{1}{2})=(2^{1-j}-1)B_{j}.$ Along with the fact that
$B_{j}(\frac{1}{2})=(2^{1-j}-1)B_{j}.$ Along with the fact that ![]() $B_{2j+1}=0$, this implies that
$B_{2j+1}=0$, this implies that ![]() $B_{2j+1}(\frac{1}{2})=0.$ Also employ the identity
$B_{2j+1}(\frac{1}{2})=0.$ Also employ the identity ![]() $\sum _{n=1}^{\infty }((-1)^{n}/(n^{2m+1}))=(2^{-2m}-1)\unicode[STIX]{x1D701}(2m+1)$. These together imply (2.11).◻
$\sum _{n=1}^{\infty }((-1)^{n}/(n^{2m+1}))=(2^{-2m}-1)\unicode[STIX]{x1D701}(2m+1)$. These together imply (2.11).◻
6 A two-parameter generalization of the transformation formula of  $\log \unicode[STIX]{x1D702}(z)$
$\log \unicode[STIX]{x1D702}(z)$
Here we prove Theorem 2.7 which is a two-parameter generalization of the transformation formula of the logarithm of the Dedekind eta function stated in (2.13).
Proof of Theorem 2.7.
Before we prove Theorem 2.7, it is important to know how it differs from Theorem 2.3. In Theorem 2.3, the condition ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \neq 0$ suggested that we separately consider the contribution
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \neq 0$ suggested that we separately consider the contribution ![]() $-(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$ arising due to the pole of
$-(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$ arising due to the pole of ![]() $\unicode[STIX]{x1D6E4}(s)$ at
$\unicode[STIX]{x1D6E4}(s)$ at ![]() $s=0$.
$s=0$.
However, in Theorem 2.7, we have the condition ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$, that is,
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$, that is, ![]() $h=\frac{N+1}{2}$, which means that the integrand
$h=\frac{N+1}{2}$, which means that the integrand ![]() $F(s)$, defined in (4.5), has a double order pole at
$F(s)$, defined in (4.5), has a double order pole at ![]() $s=0$ except when
$s=0$ except when ![]() $a=1/2$ as will be explained below. So we can as well use the same formula that we used in the proof of Theorem 2.3 to calculate the residue at the double order pole at
$a=1/2$ as will be explained below. So we can as well use the same formula that we used in the proof of Theorem 2.3 to calculate the residue at the double order pole at ![]() $s=\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \neq 0$, that is (5.1), to calculate the residue at the double order pole at
$s=\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor \neq 0$, that is (5.1), to calculate the residue at the double order pole at ![]() $s=\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$ in Theorem 2.7. But then the term
$s=\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$ in Theorem 2.7. But then the term ![]() $-(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$ appearing in Theorem 2.3 does not appear in this context. Note also that [Reference Apostol5, page 264, Equation (17)]
$-(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$ appearing in Theorem 2.3 does not appear in this context. Note also that [Reference Apostol5, page 264, Equation (17)] ![]() $\unicode[STIX]{x1D701}(0,a)=\frac{1}{2}-a\neq 0$, except when
$\unicode[STIX]{x1D701}(0,a)=\frac{1}{2}-a\neq 0$, except when ![]() $a=\frac{1}{2}$, which indeed means that we have a double order pole when
$a=\frac{1}{2}$, which indeed means that we have a double order pole when ![]() $a\neq \frac{1}{2}$. Also when
$a\neq \frac{1}{2}$. Also when ![]() $a=\frac{1}{2}$, even though we get a simple pole at
$a=\frac{1}{2}$, even though we get a simple pole at ![]() $s=0$, one can always apply (5.1) in this case too and get the correct residue contribution.
$s=0$, one can always apply (5.1) in this case too and get the correct residue contribution.
Taking the above thing into account, we let ![]() $h=\frac{N+1}{2}$ in (5.2) and simplify the resultant using the facts [Reference Temme61, page 3]
$h=\frac{N+1}{2}$ in (5.2) and simplify the resultant using the facts [Reference Temme61, page 3] ![]() $B_{1}(a)=(a-\frac{1}{2})$, [Reference Temme61, page 54]
$B_{1}(a)=(a-\frac{1}{2})$, [Reference Temme61, page 54] ![]() $\unicode[STIX]{x1D713}(1)=-\unicode[STIX]{x1D6FE}$ and [Reference Lerch43, Equations (9),
$\unicode[STIX]{x1D713}(1)=-\unicode[STIX]{x1D6FE}$ and [Reference Lerch43, Equations (9), ![]() $(22^{a})$]
$(22^{a})$] ![]() $\unicode[STIX]{x1D701}^{\prime }(0,a)=\log \unicode[STIX]{x1D6E4}(a)-\frac{1}{2}\log (2\unicode[STIX]{x1D70B})$. This results in
$\unicode[STIX]{x1D701}^{\prime }(0,a)=\log \unicode[STIX]{x1D6E4}(a)-\frac{1}{2}\log (2\unicode[STIX]{x1D70B})$. This results in
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\text{exp}(-an^{N}x)}{n(1-\text{exp}(-n^{N}x))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D701}(N+1)}{x}+\frac{1}{N}\biggl(\biggl(\frac{1}{2}-a\biggr)((N-1)\unicode[STIX]{x1D6FE}-\log x)+\log \unicode[STIX]{x1D6E4}(a)-\frac{1}{2}\log 2\unicode[STIX]{x1D70B}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}2^{N}\unicode[STIX]{x1D70B}^{N+1}\mathop{\sum }_{j=1}^{\lfloor \frac{N+1}{2N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{N+1-2jN}}{(2j)!(N+1-2jN)!}x^{2j-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{\frac{N+3}{2}}}{N}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n(\text{exp}(2A_{N,j}(\frac{n}{x}))-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}\times \bigg\{\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\bigg\}\bigg\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\text{exp}(-an^{N}x)}{n(1-\text{exp}(-n^{N}x))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D701}(N+1)}{x}+\frac{1}{N}\biggl(\biggl(\frac{1}{2}-a\biggr)((N-1)\unicode[STIX]{x1D6FE}-\log x)+\log \unicode[STIX]{x1D6E4}(a)-\frac{1}{2}\log 2\unicode[STIX]{x1D70B}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}2^{N}\unicode[STIX]{x1D70B}^{N+1}\mathop{\sum }_{j=1}^{\lfloor \frac{N+1}{2N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{N+1-2jN}}{(2j)!(N+1-2jN)!}x^{2j-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{\frac{N+3}{2}}}{N}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n(\text{exp}(2A_{N,j}(\frac{n}{x}))-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}\times \bigg\{\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\bigg\}\bigg\},\end{eqnarray}$$ where ![]() $A_{N,j}(y)$ is defined in Theorem 2.1. Now (2.12) is proved by letting
$A_{N,j}(y)$ is defined in Theorem 2.1. Now (2.12) is proved by letting ![]() $x=2^{N}\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$ in (6.1), making use of (5.9) with
$x=2^{N}\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$ in (6.1), making use of (5.9) with ![]() $m=0$ and then by simplifying the resultant.◻
$m=0$ and then by simplifying the resultant.◻
Proof of Corollary 2.8.
As mentioned in the proof of Theorem 2.7, the term ![]() $-(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$ does not appear when
$-(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$ does not appear when ![]() $\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$. With this understanding, we let
$\frac{N-2h+1}{N}=-2\lfloor \frac{h}{N}-\frac{1}{2}\rfloor =0$. With this understanding, we let ![]() $h=\frac{N+1}{2}$ in Theorem 2.3 and while simplifying, we use the following formula valid for
$h=\frac{N+1}{2}$ in Theorem 2.3 and while simplifying, we use the following formula valid for ![]() $0<a<1$ [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 45, 1.441.2]:
$0<a<1$ [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 45, 1.441.2]:
This results in
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\text{exp}(-an^{N}x)}{n(1-\text{exp}(-n^{N}x))}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FE}\biggl(\frac{1}{2}-a\biggr)-\frac{\log (2\sin (\unicode[STIX]{x1D70B}a))}{2N}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}2^{N}\unicode[STIX]{x1D70B}^{N+1}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{B_{2j}(a)B_{N+1-2jN}}{(2j)!(N+1-2jN)!}x^{2j-1}+\frac{(-1)^{\frac{N+3}{2}}}{N}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n(\text{exp}(2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+3}{2}}}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}\biggl(\unicode[STIX]{x1D713}\biggl(i\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D713}\biggl(-i\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\text{exp}(-an^{N}x)}{n(1-\text{exp}(-n^{N}x))}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FE}\biggl(\frac{1}{2}-a\biggr)-\frac{\log (2\sin (\unicode[STIX]{x1D70B}a))}{2N}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{\frac{N+3}{2}}2^{N}\unicode[STIX]{x1D70B}^{N+1}\mathop{\sum }_{j=0}^{\lfloor \frac{N+1}{2N}\rfloor }\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{B_{2j}(a)B_{N+1-2jN}}{(2j)!(N+1-2jN)!}x^{2j-1}+\frac{(-1)^{\frac{N+3}{2}}}{N}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n(\text{exp}(2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{j+\frac{N+3}{2}}}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}\biggl(\unicode[STIX]{x1D713}\biggl(i\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D713}\biggl(-i\biggl(\frac{2\unicode[STIX]{x1D70B}n}{x}\biggr)^{\frac{1}{N}}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}}\biggr)\biggr)\bigg\}.\end{eqnarray}$$ Now let ![]() $x=2^{N}\unicode[STIX]{x1D6FC}$ and
$x=2^{N}\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$ in (6.2) and simplify so as to obtain (2.14).◻
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$ in (6.2) and simplify so as to obtain (2.14).◻
Proof. Let ![]() $N=1,a=1/2$,
$N=1,a=1/2$, ![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}$ in (2.14) and simplify.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}$ in (2.14) and simplify.
Equation (6.3), given in an equivalent form in [Reference Berndt7, page 169], is a special case of a result in Ramanujan’s Notebooks [Reference Ramanujan55, Vol. I, page 257, no. 12; Vol. II, page 169, no. 8(ii)] which was rediscovered by Lagrange [Reference Lagrange42]. See [Reference Berndt7, pages 168–169] for more details.
7 Proof of Theorem 2.10 and its special cases
Proof of Theorem 2.10.
Since the proof is similar to that of Theorem 2.1, we will be brief.
As before, (4.4) holds, but now for ![]() $\text{Re}(s)=l>\max (\frac{N-2h+1}{N},1)$. We choose the contour
$\text{Re}(s)=l>\max (\frac{N-2h+1}{N},1)$. We choose the contour ![]() $[\unicode[STIX]{x1D706}-iT,\unicode[STIX]{x1D706}+iT],[\unicode[STIX]{x1D706}+iT,-r+iT],[-r+iT,-r-iT]$ and
$[\unicode[STIX]{x1D706}-iT,\unicode[STIX]{x1D706}+iT],[\unicode[STIX]{x1D706}+iT,-r+iT],[-r+iT,-r-iT]$ and ![]() $[-r-iT,\unicode[STIX]{x1D706}-iT]$, where,
$[-r-iT,\unicode[STIX]{x1D706}-iT]$, where, ![]() $r$ is a positive real number such that
$r$ is a positive real number such that ![]() $0<r<\frac{1}{N}$, the reason for which will be clear soon. The poles of the integrand
$0<r<\frac{1}{N}$, the reason for which will be clear soon. The poles of the integrand ![]() $F(s)$, defined in (4.5), that are enclosed in the contour are the simple poles at
$F(s)$, defined in (4.5), that are enclosed in the contour are the simple poles at ![]() $s=0,1$ and
$s=0,1$ and ![]() $\frac{N-2h+1}{N}$, the residues of whom are same as those calculated in (4.6), (4.7) and (4.8), respectively. Thus, using Cauchy’s residue theorem, letting
$\frac{N-2h+1}{N}$, the residues of whom are same as those calculated in (4.6), (4.7) and (4.8), respectively. Thus, using Cauchy’s residue theorem, letting ![]() $T\rightarrow \infty$ and noting that the integrals along the horizontal segments approach zero, and invoking (4.4), we see that
$T\rightarrow \infty$ and noting that the integrals along the horizontal segments approach zero, and invoking (4.4), we see that
where ![]() $J(x,a)$ is defined in (4.12). We first prove part (i), that is, when
$J(x,a)$ is defined in (4.12). We first prove part (i), that is, when ![]() $N$ is an odd positive integer. From (4.12) to (4.23), the calculations for evaluating
$N$ is an odd positive integer. From (4.12) to (4.23), the calculations for evaluating ![]() $J(x,a)$ remain exactly the same. Now (4.18) and the inequality
$J(x,a)$ remain exactly the same. Now (4.18) and the inequality ![]() $0<r<1/N$ along with the fact that
$0<r<1/N$ along with the fact that ![]() $\text{Re}(s)=1+r$ imply
$\text{Re}(s)=1+r$ imply ![]() $N-2h+1<c_{1}:=\text{Re}(s_{1})<N-2h+2$. In order to apply Lemma 4.1, we need to again shift the line of integration from
$N-2h+1<c_{1}:=\text{Re}(s_{1})<N-2h+2$. In order to apply Lemma 4.1, we need to again shift the line of integration from ![]() $\text{Re}(s_{1})=c_{1}$ to
$\text{Re}(s_{1})=c_{1}$ to ![]() $\text{Re}(s_{1})=c_{2}$, where
$\text{Re}(s_{1})=c_{2}$, where ![]() $0<c_{2}<2$. In doing so, we encounter poles of the integrand
$0<c_{2}<2$. In doing so, we encounter poles of the integrand ![]() $\frac{\unicode[STIX]{x1D6E4}(s_{1})}{\tan (\frac{\unicode[STIX]{x1D70B}s_{1}}{2})}{X_{m,n,j}^{\ast }}^{-s_{1}}$ at
$\frac{\unicode[STIX]{x1D6E4}(s_{1})}{\tan (\frac{\unicode[STIX]{x1D70B}s_{1}}{2})}{X_{m,n,j}^{\ast }}^{-s_{1}}$ at ![]() $s=2,4,\ldots ,N-2h+1$. Again, the integrals along the horizontal segments approach zero as the height of the contour tends to
$s=2,4,\ldots ,N-2h+1$. Again, the integrals along the horizontal segments approach zero as the height of the contour tends to ![]() $\infty$. Now
$\infty$. Now
along with Lemma 4.1 and (4.22) imply that
 $$\begin{eqnarray}\displaystyle E(X_{m,n}) & = & \displaystyle \frac{(-1)^{\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{0}^{\infty }\frac{t\cos t}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,\text{d}t+\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\unicode[STIX]{x1D6E4}(2k){X_{m,n,j}^{\ast }}^{-2k}\biggr)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E(X_{m,n}) & = & \displaystyle \frac{(-1)^{\frac{N+1}{2}}}{\unicode[STIX]{x1D70B}}\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{0}^{\infty }\frac{t\cos t}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,\text{d}t+\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\unicode[STIX]{x1D6E4}(2k){X_{m,n,j}^{\ast }}^{-2k}\biggr)\nonumber\end{eqnarray}$$so that along with (4.19), we have
 $$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle \frac{2}{\unicode[STIX]{x1D70B}Nx}(-1)^{h+\frac{N+3}{2}}(2\unicode[STIX]{x1D70B})^{2h}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{\frac{1-2h}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\mathop{\sum }_{n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{m=1}^{\infty }\biggl(\int _{0}^{\infty }\frac{t\cos (t)}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,dt+\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\unicode[STIX]{x1D6E4}(2k){X_{m,n,j}^{\ast }}^{-2k}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{2}(x,a) & = & \displaystyle \frac{2}{\unicode[STIX]{x1D70B}Nx}(-1)^{h+\frac{N+3}{2}}(2\unicode[STIX]{x1D70B})^{2h}\biggl(\frac{(2\unicode[STIX]{x1D70B})^{N+1}}{x}\biggr)^{\frac{1-2h}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{j=-(N-1)}^{N-1}i^{j}e^{\frac{-ij\unicode[STIX]{x1D70B}(2h-1)}{2N}}\mathop{\sum }_{n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{m=1}^{\infty }\biggl(\int _{0}^{\infty }\frac{t\cos (t)}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,dt+\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\unicode[STIX]{x1D6E4}(2k){X_{m,n,j}^{\ast }}^{-2k}\biggr).\end{eqnarray}$$Employ Theorem 2.2 using (4.23) and (4.21) to see that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m=1}^{\infty }\biggl(\int _{0}^{\infty }\frac{t\cos (t)}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,dt+\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\unicode[STIX]{x1D6E4}(2k){X_{m,n,j}^{\ast }}^{-2k}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\biggl(\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,T(N,h,x,j)\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m=1}^{\infty }\biggl(\int _{0}^{\infty }\frac{t\cos (t)}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,dt+\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\unicode[STIX]{x1D6E4}(2k){X_{m,n,j}^{\ast }}^{-2k}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\biggl(\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,T(N,h,x,j)\biggr),\end{eqnarray}$$where
 $$\begin{eqnarray}T(N,h,x,j):=2\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\frac{\unicode[STIX]{x1D6E4}(2k)\unicode[STIX]{x1D701}(2k)}{(2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{1/N}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})^{2k}}.\end{eqnarray}$$
$$\begin{eqnarray}T(N,h,x,j):=2\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\frac{\unicode[STIX]{x1D6E4}(2k)\unicode[STIX]{x1D701}(2k)}{(2\unicode[STIX]{x1D70B}(\frac{2\unicode[STIX]{x1D70B}n}{x})^{1/N}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})^{2k}}.\end{eqnarray}$$ From [Reference Abramowitz and Stegun1, page 259, formula 6.3.18], for ![]() $|\text{arg}\,z|<\unicode[STIX]{x1D70B}$, as
$|\text{arg}\,z|<\unicode[STIX]{x1D70B}$, as ![]() $z\rightarrow \infty$,
$z\rightarrow \infty$,
This implies
 $$\begin{eqnarray}\displaystyle & & \displaystyle \log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =O_{N,x}(n^{-2/N}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)-\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =O_{N,x}(n^{-2/N}),\nonumber\end{eqnarray}$$ and since ![]() $1\leqslant k\leqslant \frac{N-2h+1}{2}$,
$1\leqslant k\leqslant \frac{N-2h+1}{2}$, ![]() $T(N,h,x,j)=O_{N,x}(n^{-2/N})$. Thus if we multiply both sides of (7.3) by
$T(N,h,x,j)=O_{N,x}(n^{-2/N})$. Thus if we multiply both sides of (7.3) by ![]() $n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)$ and then sum over
$n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)$ and then sum over ![]() $n$, we can write the sum as
$n$, we can write the sum as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{m=1}^{\infty }\biggl(\int _{0}^{\infty }\frac{t\cos (t)}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,dt+\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\unicode[STIX]{x1D6E4}(2k){X_{m,n,j}^{\ast }}^{-2k}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\bigg\{\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}T(N,h,x,j),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{\frac{1-2h}{N}}\sin (2\unicode[STIX]{x1D70B}na)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{m=1}^{\infty }\biggl(\int _{0}^{\infty }\frac{t\cos (t)}{{X_{m,n,j}^{\ast }}^{2}+t^{2}}\,dt+\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\unicode[STIX]{x1D6E4}(2k){X_{m,n,j}^{\ast }}^{-2k}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}\bigg\{\log \biggl(\frac{1}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{2}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i}{\unicode[STIX]{x1D70B}}A_{N,j}\biggl(\frac{n}{x}\biggr)\biggr)\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}T(N,h,x,j),\end{eqnarray}$$ since the series ![]() $\sum _{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h+1}{N}}}$ converges for
$\sum _{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h+1}{N}}}$ converges for ![]() $0<a\leqslant 1$ as long as
$0<a\leqslant 1$ as long as ![]() $(2h+1)/N>0$, that is,
$(2h+1)/N>0$, that is, ![]() $h\geqslant 0$, which is what we have in our hypotheses. (This also explains why we fail to obtain a transformation for our series when
$h\geqslant 0$, which is what we have in our hypotheses. (This also explains why we fail to obtain a transformation for our series when ![]() $h<0$.)
$h<0$.)
Now substituting (7.5) in (7.2), noting that the expression for ![]() $J_{1}(x,a)$ remains exactly as in (4.27), we deduce along with (7.1), (4.6), (4.7), (4.8) and (4.15) that for
$J_{1}(x,a)$ remains exactly as in (4.27), we deduce along with (7.1), (4.6), (4.7), (4.8) and (4.15) that for ![]() $0<a\leqslant 1$,
$0<a\leqslant 1$,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}\nonumber\\ \displaystyle & & \displaystyle \quad =-\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h)+\frac{\unicode[STIX]{x1D701}(2h)}{x}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{N-2h+1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{N-2h+1}{N},a\biggr)x^{-\frac{(N-2h+1)}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,S(x,a)+\frac{(-1)^{h+\frac{N+3}{2}}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\text{exp}\biggl(\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}T(N,h,x,j).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}\nonumber\\ \displaystyle & & \displaystyle \quad =-\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h)+\frac{\unicode[STIX]{x1D701}(2h)}{x}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{N-2h+1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{N-2h+1}{N},a\biggr)x^{-\frac{(N-2h+1)}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,S(x,a)+\frac{(-1)^{h+\frac{N+3}{2}}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}\text{exp}\biggl(\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}\biggr)\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}T(N,h,x,j).\end{eqnarray}$$ Thus (7.6) leads to (2.16) for ![]() $a=1$ with
$a=1$ with ![]() $g(N,h,1)=-\frac{1}{2}\unicode[STIX]{x1D701}(-N+2h)$.
$g(N,h,1)=-\frac{1}{2}\unicode[STIX]{x1D701}(-N+2h)$.
When ![]() $0<a<1$, in view of (2.15), (2.16) and (7.6), it suffices to show that
$0<a<1$, in view of (2.15), (2.16) and (7.6), it suffices to show that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(-1)^{h+\frac{N+3}{2}}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}T(N,h,x,j)\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(-1)^{h+\frac{N+3}{2}}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)j}{N}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h-1}{N}}}T(N,h,x,j)\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(-N+2h).\end{eqnarray}$$ Use Euler’s formula (2.9) along with ![]() $\unicode[STIX]{x1D701}(1-2k)=-B_{2k}/(2k)$, or equivalently, use the functional equation for
$\unicode[STIX]{x1D701}(1-2k)=-B_{2k}/(2k)$, or equivalently, use the functional equation for ![]() $\unicode[STIX]{x1D701}(2k)$ to simplify
$\unicode[STIX]{x1D701}(2k)$ to simplify ![]() $T(N,h,x,j)$ as
$T(N,h,x,j)$ as
 $$\begin{eqnarray}T(N,h,x,j)=\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\frac{(-1)^{k}\unicode[STIX]{x1D701}(1-2k)}{((\frac{2\unicode[STIX]{x1D70B}n}{x})^{1/N}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})^{2k}}.\end{eqnarray}$$
$$\begin{eqnarray}T(N,h,x,j)=\mathop{\sum }_{k=1}^{\frac{N-2h+1}{2}}\frac{(-1)^{k}\unicode[STIX]{x1D701}(1-2k)}{((\frac{2\unicode[STIX]{x1D70B}n}{x})^{1/N}e^{\frac{i\unicode[STIX]{x1D70B}j}{N}})^{2k}}.\end{eqnarray}$$ Now substitute the above representation of ![]() $T(N,h,x,j)$ in (7.7), separate the term corresponding to
$T(N,h,x,j)$ in (7.7), separate the term corresponding to ![]() $k=\frac{N-2h+1}{2}$ on the left side and invoke [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 45, Formula 1.441.1]
$k=\frac{N-2h+1}{2}$ on the left side and invoke [Reference Gradshteyn, Ryzhik, Zwillinger and Moll26, page 45, Formula 1.441.1] ![]() $\sum _{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}=-\unicode[STIX]{x1D70B}(a-\frac{1}{2})$ to see that this term equals
$\sum _{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n}=-\unicode[STIX]{x1D70B}(a-\frac{1}{2})$ to see that this term equals ![]() $(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$. Thus we need only show that
$(a-\frac{1}{2})\unicode[STIX]{x1D701}(-N+2h)$. Thus we need only show that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(-1)^{h+\frac{N+3}{2}}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{k=1}^{\frac{N-2h-1}{2}}\frac{(-1)^{k}\unicode[STIX]{x1D701}(1-2k)}{(\frac{2\unicode[STIX]{x1D70B}}{x})^{2k/N}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h+2k-1}{N}}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h-2k)j}{N}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(-1)^{h+\frac{N+3}{2}}}{\unicode[STIX]{x1D70B}N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{N-2h+1}{N}}\mathop{\sum }_{k=1}^{\frac{N-2h-1}{2}}\frac{(-1)^{k}\unicode[STIX]{x1D701}(1-2k)}{(\frac{2\unicode[STIX]{x1D70B}}{x})^{2k/N}}\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{\frac{2h+2k-1}{N}}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h-2k)j}{N}}=0.\end{eqnarray}$$ In the sum in (4.2), replace ![]() $j$ by
$j$ by ![]() $2j$, then let
$2j$, then let ![]() $z=\frac{\unicode[STIX]{x1D70B}}{2N}(2h+2k-1)$ so that
$z=\frac{\unicode[STIX]{x1D70B}}{2N}(2h+2k-1)$ so that
 $$\begin{eqnarray}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h-2k)j}{N}}=\frac{\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2})}{\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2N})}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=-\frac{(N-1)}{2}}^{\frac{(N-1)}{2}}(-1)^{j}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h-2k)j}{N}}=\frac{\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2})}{\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2N})}.\end{eqnarray}$$ Now ![]() $\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2})=0$, but we should also show
$\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2})=0$, but we should also show ![]() $\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2N})\neq 0$. To that end, note that
$\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2N})\neq 0$. To that end, note that ![]() $1\leqslant k<\frac{N-2h+1}{2}$ implies
$1\leqslant k<\frac{N-2h+1}{2}$ implies ![]() $\frac{2h+1}{N}\leqslant \frac{2h+2k-1}{N}<1$. Also,
$\frac{2h+1}{N}\leqslant \frac{2h+2k-1}{N}<1$. Also, ![]() $h\geqslant 0$ implies
$h\geqslant 0$ implies ![]() $\frac{2h+1}{N}\geqslant \frac{1}{N}$. Combining, we see that
$\frac{2h+1}{N}\geqslant \frac{1}{N}$. Combining, we see that ![]() $\frac{1}{N}\leqslant \frac{2h+2k-1}{N}<1$, so that
$\frac{1}{N}\leqslant \frac{2h+2k-1}{N}<1$, so that ![]() $\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2N})\neq 0$ for
$\cos (\frac{\unicode[STIX]{x1D70B}(2h+2k-1)}{2N})\neq 0$ for ![]() $N>1$. Thus, the sum over
$N>1$. Thus, the sum over ![]() $j$ in (7.9) equals
$j$ in (7.9) equals ![]() $0$ for
$0$ for ![]() $N>1$ which implies (7.8). For
$N>1$ which implies (7.8). For ![]() $N=1$, note that
$N=1$, note that ![]() $h<N/2$ along with
$h<N/2$ along with ![]() $h\geqslant 0$ implies
$h\geqslant 0$ implies ![]() $h=0$ so that the sum over
$h=0$ so that the sum over ![]() $k$ in (7.8) is empty, and hence (7.8) holds again. Hence (7.7) holds and thus (2.16) is valid with
$k$ in (7.8) is empty, and hence (7.8) holds again. Hence (7.7) holds and thus (2.16) is valid with ![]() $g(N,h,a)=0$ for
$g(N,h,a)=0$ for ![]() $0<a<1$.
$0<a<1$.
We omit the proof of (2.17) since it is exactly along the lines of the proof of Theorem 2.1. By a similar argument one sees that (2.17) holds also when ![]() $h<0$, unlike when
$h<0$, unlike when ![]() $N$ is odd.◻
$N$ is odd.◻
Proof of Corollary 2.11.
Let ![]() $N=1$ so that
$N=1$ so that ![]() $h=0$ in part (i) of Theorem 2.10. Use the fact [Reference Olver, Lozier, Boisvert and Clark51, page 608, Formula 25.11.12]
$h=0$ in part (i) of Theorem 2.10. Use the fact [Reference Olver, Lozier, Boisvert and Clark51, page 608, Formula 25.11.12] ![]() $\unicode[STIX]{x1D701}(\ell ,a)=\frac{(-1)^{\ell }}{(\ell -1)!}\unicode[STIX]{x1D713}^{(\ell -1)}(a)$, let
$\unicode[STIX]{x1D701}(\ell ,a)=\frac{(-1)^{\ell }}{(\ell -1)!}\unicode[STIX]{x1D713}^{(\ell -1)}(a)$, let ![]() $x=2\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$ and simplify.◻
$x=2\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$ and simplify.◻
8 A vast generalization of Wigert’s formula for  $\unicode[STIX]{x1D701}(\frac{1}{N})$
$\unicode[STIX]{x1D701}(\frac{1}{N})$
Except for Theorems 2.1 and 2.10, we have mostly concentrated on results for an odd positive integer ![]() $N$. In this section, we give results for
$N$. In this section, we give results for ![]() $N$ even. We begin with the proof of a two-parameter generalization of Wigert’s formula [Reference Wigert67, pages 8–9, Equation (5)], [Reference Dixit and Maji21, Equation (1.2)].
$N$ even. We begin with the proof of a two-parameter generalization of Wigert’s formula [Reference Wigert67, pages 8–9, Equation (5)], [Reference Dixit and Maji21, Equation (1.2)].
Proof of Theorem 2.12.
Here ![]() $N$ is an even positive integer. We first prove the result for a nonnegative integer
$N$ is an even positive integer. We first prove the result for a nonnegative integer ![]() $m$ using Theorem 2.1. For
$m$ using Theorem 2.1. For ![]() $m<0$, it can be proved using Theorem 2.10.
$m<0$, it can be proved using Theorem 2.10.
Suppose ![]() $m$ is a nonnegative integer. Then let
$m$ is a nonnegative integer. Then let ![]() $h=\frac{N}{2}+Nm$,
$h=\frac{N}{2}+Nm$, ![]() $x=2^{N}\unicode[STIX]{x1D6FC}$ in Theorem 2.1 and let
$x=2^{N}\unicode[STIX]{x1D6FC}$ in Theorem 2.1 and let ![]() $\unicode[STIX]{x1D6FD}>0$ be defined by
$\unicode[STIX]{x1D6FD}>0$ be defined by ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$. After rearranging some terms, we obtain
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$. After rearranging some terms, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(2Nm)+\mathop{\sum }_{j=1}^{m}\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2N(m-j))(2^{N}\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm}\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\exp (-(2n)^{N}\unicode[STIX]{x1D6FC})}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{1-2Nm}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{1-2Nm}{N},a\biggr)(2^{N}\unicode[STIX]{x1D6FC})^{\frac{2Nm-1}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{\frac{N}{2}+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{2^{N}\unicode[STIX]{x1D6FC}}\biggr)^{\frac{1-2Nm}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}\exp \biggl(-\frac{i\unicode[STIX]{x1D70B}}{2}(2m+1)(2j+1)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+\frac{N}{2}+1}\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}(\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{\frac{N}{2}+1}}{2}(2\unicode[STIX]{x1D70B})^{N+2Nm}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=0}^{m}\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{N+2N(m-j)}}{(2j)!(N+2N(m-j))!}(2^{N}\unicode[STIX]{x1D6FC})^{2j-1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(a-\frac{1}{2}\biggr)\unicode[STIX]{x1D701}(2Nm)+\mathop{\sum }_{j=1}^{m}\frac{B_{2j+1}(a)}{(2j+1)!}\unicode[STIX]{x1D701}(2N(m-j))(2^{N}\unicode[STIX]{x1D6FC})^{2j}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{n=1}^{\infty }\frac{n^{-2Nm}\text{exp}(-a(2n)^{N}\unicode[STIX]{x1D6FC})}{1-\exp (-(2n)^{N}\unicode[STIX]{x1D6FC})}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{1-2Nm}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{1-2Nm}{N},a\biggr)(2^{N}\unicode[STIX]{x1D6FC})^{\frac{2Nm-1}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{\frac{N}{2}+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{2^{N}\unicode[STIX]{x1D6FC}}\biggr)^{\frac{1-2Nm}{N}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}\exp \biggl(-\frac{i\unicode[STIX]{x1D70B}}{2}(2m+1)(2j+1)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+\frac{N}{2}+1}\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}(\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{\frac{N}{2}+1}}{2}(2\unicode[STIX]{x1D70B})^{N+2Nm}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{j=0}^{m}\biggl(\frac{-1}{4\unicode[STIX]{x1D70B}^{2}}\biggr)^{jN}\frac{B_{2j}(a)B_{N+2N(m-j)}}{(2j)!(N+2N(m-j))!}(2^{N}\unicode[STIX]{x1D6FC})^{2j-1},\end{eqnarray}$$ where we have used the fact ![]() $2A_{N,j+\frac{1}{2}}(\frac{n}{x})=(2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}$.
$2A_{N,j+\frac{1}{2}}(\frac{n}{x})=(2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}$.
We now simplify some of the expressions on the right-hand side. Since ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{N}=\unicode[STIX]{x1D70B}^{N+1}$,
We now split the sum ![]() $\sum _{j=-\frac{N}{2}}^{\frac{N}{2}-1}=\sum _{j=0}^{\frac{N}{2}-1}+\sum _{j=-\frac{N}{2}}^{-1}$ and replace
$\sum _{j=-\frac{N}{2}}^{\frac{N}{2}-1}=\sum _{j=0}^{\frac{N}{2}-1}+\sum _{j=-\frac{N}{2}}^{-1}$ and replace ![]() $j$ by
$j$ by ![]() $-1-j$ in the second sum. Then combining the corresponding terms in the resulting two finite sums on the above right-hand side, using the fact that
$-1-j$ in the second sum. Then combining the corresponding terms in the resulting two finite sums on the above right-hand side, using the fact that ![]() $\exp (-\frac{1}{2}(i\unicode[STIX]{x1D70B}(2j+1)(2m+1)))=i(-1)^{j+m+1}$ and then simplifying, we get
$\exp (-\frac{1}{2}(i\unicode[STIX]{x1D70B}(2j+1)(2m+1)))=i(-1)^{j+m+1}$ and then simplifying, we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}\exp \biggl(-\frac{i\unicode[STIX]{x1D70B}}{2}(2m+1)(2j+1)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+\frac{N}{2}+1}\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}(\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1)}\nonumber\\ \displaystyle & & \displaystyle \quad =-2(-1)^{m+1}\mathop{\sum }_{j=0}^{\frac{N}{2}-1}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl[\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}}\text{Im}\biggl(\frac{e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}}{\exp ((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{j+\frac{N}{2}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}}\text{Re}\biggl(\frac{e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}}{\exp ((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1}\biggr)\biggr].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}\exp \biggl(-\frac{i\unicode[STIX]{x1D70B}}{2}(2m+1)(2j+1)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+\frac{N}{2}+1}\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}(\text{exp}((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1)}\nonumber\\ \displaystyle & & \displaystyle \quad =-2(-1)^{m+1}\mathop{\sum }_{j=0}^{\frac{N}{2}-1}(-1)^{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl[\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}}\text{Im}\biggl(\frac{e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}}{\exp ((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{j+\frac{N}{2}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{n^{2m+1-\frac{1}{N}}}\text{Re}\biggl(\frac{e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}}}{\exp ((2n)^{\frac{1}{N}}\unicode[STIX]{x1D6FD}e^{\frac{i\unicode[STIX]{x1D70B}(2j+1)}{2N}})-1}\biggr)\biggr].\end{eqnarray}$$ Now substituting (8.4) in (8.1), using (8.2) and (8.3), and then multiplying both sides of the resulting identity by ![]() $\unicode[STIX]{x1D6FC}^{-(\frac{2Nm-1}{N+1})}$, we arrive at (2.19). This completes the proof for
$\unicode[STIX]{x1D6FC}^{-(\frac{2Nm-1}{N+1})}$, we arrive at (2.19). This completes the proof for ![]() $m>0$. For
$m>0$. For ![]() $m<0$, the result follows from part (ii) of Theorem 2.10. The argument is exactly the same as above and is hence omitted.◻
$m<0$, the result follows from part (ii) of Theorem 2.10. The argument is exactly the same as above and is hence omitted.◻
Remark 9. For ![]() $h\geqslant N/2$,
$h\geqslant N/2$, ![]() $N$ even, we considered
$N$ even, we considered ![]() $h=\frac{N}{2}+Nm,m\in \mathbb{N}\cup \{0\}$ in the proof of Theorem 2.12 given above. However, one can even consider a more general
$h=\frac{N}{2}+Nm,m\in \mathbb{N}\cup \{0\}$ in the proof of Theorem 2.12 given above. However, one can even consider a more general ![]() $h$ of the form
$h$ of the form ![]() $h=\frac{N}{2}+Nm+r,0\leqslant r<N$ and derive identities analogous to Theorem 2.12.
$h=\frac{N}{2}+Nm+r,0\leqslant r<N$ and derive identities analogous to Theorem 2.12.
Even though Theorem 2.13 can be proved using Theorem 2.12, we prefer to give the proof using Theorem 2.1 because the conditions on ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FD}$ in the former two theorems are different. We begin with an analogue of Lemma 4.4 to be used in the proof of Theorem 2.13.
$\unicode[STIX]{x1D6FD}$ in the former two theorems are different. We begin with an analogue of Lemma 4.4 to be used in the proof of Theorem 2.13.
Lemma 8.1. For ![]() $a,u,v\in \mathbb{R}$, we have
$a,u,v\in \mathbb{R}$, we have
We omit the proof since it can be proved similarly as Lemma 4.4 given in [Reference Dixit and Maji21].
Proof of Theorem 2.13.
Let ![]() $h=\frac{N}{2}$ in Theorem 2.1. This gives
$h=\frac{N}{2}$ in Theorem 2.1. This gives
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\exp (-an^{N}x)}{1-\exp (-n^{N}x)} & = & \displaystyle \frac{1}{2}\biggl(a-\frac{1}{2}\biggr)+\frac{\unicode[STIX]{x1D701}(N)}{x}+\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{1}{N},a\biggr)x^{-\frac{1}{N}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{\frac{N}{2}+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{1}{N}}\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)(j+\frac{1}{2})}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+\frac{N}{2}+1}\sin (2\unicode[STIX]{x1D70B}na)}{n^{1-\frac{1}{N}}(\text{exp}(2A_{N,j+\frac{1}{2}}(\frac{n}{x}))-1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\exp (-an^{N}x)}{1-\exp (-n^{N}x)} & = & \displaystyle \frac{1}{2}\biggl(a-\frac{1}{2}\biggr)+\frac{\unicode[STIX]{x1D701}(N)}{x}+\frac{1}{N}\unicode[STIX]{x1D6E4}\biggl(\frac{1}{N}\biggr)\unicode[STIX]{x1D701}\biggl(\frac{1}{N},a\biggr)x^{-\frac{1}{N}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{\frac{N}{2}+1}}{N}\biggl(\frac{2\unicode[STIX]{x1D70B}}{x}\biggr)^{\frac{1}{N}}\mathop{\sum }_{j=-\frac{N}{2}}^{\frac{N}{2}-1}e^{\frac{i\unicode[STIX]{x1D70B}(1-2h)(j+\frac{1}{2})}{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)+i(-1)^{j+\frac{N}{2}+1}\sin (2\unicode[STIX]{x1D70B}na)}{n^{1-\frac{1}{N}}(\text{exp}(2A_{N,j+\frac{1}{2}}(\frac{n}{x}))-1)}.\nonumber\end{eqnarray}$$ Wigert’s formula [Reference Wigert67, pages 8–9, Equation (5)] (see also [Reference Dixit and Maji21, Equation (1.2)]) is a special case of the above formula when ![]() $a=1$.
$a=1$.
Now let ![]() $N=2$ and simplify so as to obtain
$N=2$ and simplify so as to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\exp (-an^{2}x)}{1-\exp (-n^{2}x)}=\frac{1}{2}\biggl(a-\frac{1}{2}\biggr)+\frac{\unicode[STIX]{x1D70B}^{2}}{6x}+\frac{1}{2}\sqrt{\frac{\unicode[STIX]{x1D70B}}{x}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2},a\biggr)+\sqrt{\frac{2\unicode[STIX]{x1D70B}}{x}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl[\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\text{Re}\biggl(\frac{\exp (i\unicode[STIX]{x1D70B}/4)}{\exp ((2\unicode[STIX]{x1D70B})^{\frac{3}{2}}\sqrt{\frac{n}{x}}e^{-\frac{i\unicode[STIX]{x1D70B}}{4}})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\text{Im}\biggl(\frac{\exp (i\unicode[STIX]{x1D70B}/4)}{\exp ((2\unicode[STIX]{x1D70B})^{\frac{3}{2}}\sqrt{\frac{n}{x}}e^{-\frac{i\unicode[STIX]{x1D70B}}{4}})-1}\biggr)\biggr].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\exp (-an^{2}x)}{1-\exp (-n^{2}x)}=\frac{1}{2}\biggl(a-\frac{1}{2}\biggr)+\frac{\unicode[STIX]{x1D70B}^{2}}{6x}+\frac{1}{2}\sqrt{\frac{\unicode[STIX]{x1D70B}}{x}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2},a\biggr)+\sqrt{\frac{2\unicode[STIX]{x1D70B}}{x}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl[\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\text{Re}\biggl(\frac{\exp (i\unicode[STIX]{x1D70B}/4)}{\exp ((2\unicode[STIX]{x1D70B})^{\frac{3}{2}}\sqrt{\frac{n}{x}}e^{-\frac{i\unicode[STIX]{x1D70B}}{4}})-1}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\text{Im}\biggl(\frac{\exp (i\unicode[STIX]{x1D70B}/4)}{\exp ((2\unicode[STIX]{x1D70B})^{\frac{3}{2}}\sqrt{\frac{n}{x}}e^{-\frac{i\unicode[STIX]{x1D70B}}{4}})-1}\biggr)\biggr].\end{eqnarray}$$ Letting ![]() $a=1$ and using Lemmas 4.4 and 8.1, we obtain a formula of Ramanujan [Reference Ramanujan55], [Reference Berndt8, page 314], [Reference Ramanujan56, page 332]:
$a=1$ and using Lemmas 4.4 and 8.1, we obtain a formula of Ramanujan [Reference Ramanujan55], [Reference Berndt8, page 314], [Reference Ramanujan56, page 332]:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{1}{\exp (n^{2}x)-1}=\frac{1}{4}+\frac{\unicode[STIX]{x1D70B}^{2}}{6x}+\frac{1}{2}\sqrt{\frac{\unicode[STIX]{x1D70B}}{x}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}\biggr)+\sqrt{\frac{\unicode[STIX]{x1D70B}}{2x}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{1}{\sqrt{n}}\biggl(\frac{\cos (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}}+\frac{\unicode[STIX]{x1D70B}}{4})-e^{-2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}}}\cos (\frac{\unicode[STIX]{x1D70B}}{4})}{\cosh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})-\cos (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{1}{\exp (n^{2}x)-1}=\frac{1}{4}+\frac{\unicode[STIX]{x1D70B}^{2}}{6x}+\frac{1}{2}\sqrt{\frac{\unicode[STIX]{x1D70B}}{x}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}\biggr)+\sqrt{\frac{\unicode[STIX]{x1D70B}}{2x}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{n=1}^{\infty }\frac{1}{\sqrt{n}}\biggl(\frac{\cos (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}}+\frac{\unicode[STIX]{x1D70B}}{4})-e^{-2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}}}\cos (\frac{\unicode[STIX]{x1D70B}}{4})}{\cosh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})-\cos (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}\biggr).\end{eqnarray}$$ For ![]() $0<a<1$, one is able to further simplify (8.5). To that end, keeping in mind that (1.4) holds also for
$0<a<1$, one is able to further simplify (8.5). To that end, keeping in mind that (1.4) holds also for ![]() $\text{Re}(s)<1$, we let
$\text{Re}(s)<1$, we let ![]() $s=1/2$ in it to obtain
$s=1/2$ in it to obtain
Invoking (8.7) in (8.5), then simplifying using Lemmas 4.4 and 8.1 leads to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\exp (-an^{2}x)}{1-\exp (-n^{2}x)}=\frac{1}{2}\biggl(a-\frac{1}{2}\biggr)+\frac{\unicode[STIX]{x1D70B}^{2}}{6x}+\frac{1}{2}\sqrt{\frac{\unicode[STIX]{x1D70B}}{x}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl[\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\biggl(\frac{\sinh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})-\sin (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}{\cosh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})-\cos (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\biggl(\frac{\sinh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})+\sin (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}{\cosh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})-\cos (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}\biggr)\biggr].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\exp (-an^{2}x)}{1-\exp (-n^{2}x)}=\frac{1}{2}\biggl(a-\frac{1}{2}\biggr)+\frac{\unicode[STIX]{x1D70B}^{2}}{6x}+\frac{1}{2}\sqrt{\frac{\unicode[STIX]{x1D70B}}{x}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl[\mathop{\sum }_{n=1}^{\infty }\frac{\cos (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\biggl(\frac{\sinh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})-\sin (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}{\cosh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})-\cos (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{n=1}^{\infty }\frac{\sin (2\unicode[STIX]{x1D70B}na)}{\sqrt{n}}\biggl(\frac{\sinh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})+\sin (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}{\cosh (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})-\cos (2\unicode[STIX]{x1D70B}^{\frac{3}{2}}\sqrt{\frac{n}{x}})}\biggr)\biggr].\nonumber\end{eqnarray}$$ Finally, let ![]() $x=\unicode[STIX]{x1D6FC}$ and let
$x=\unicode[STIX]{x1D6FC}$ and let ![]() $\unicode[STIX]{x1D6FD}=4\unicode[STIX]{x1D70B}^{3}/\unicode[STIX]{x1D6FC}$ to arrive at (2.20). To derive (2.21), let
$\unicode[STIX]{x1D6FD}=4\unicode[STIX]{x1D70B}^{3}/\unicode[STIX]{x1D6FC}$ to arrive at (2.20). To derive (2.21), let ![]() $a=1/2$ in (2.20).◻
$a=1/2$ in (2.20).◻
Remark 10. Another generalization of Ramanujan’s formula (8.6), quite different from (8.5), is obtained in [Reference Berndt, Dixit, Roy and Zaharescu11, page 859, Theorem 10.1].
9 Applications
The arithmetic nature of Euler’s constant is quite mysterious. It is not even known if ![]() $\unicode[STIX]{x1D6FE}$ is irrational. For a very interesting and in-depth article on this constant, we refer the reader to a recent paper by Lagarias [Reference Lagarias41]. Corollary 2.8 gives the following result on
$\unicode[STIX]{x1D6FE}$ is irrational. For a very interesting and in-depth article on this constant, we refer the reader to a recent paper by Lagarias [Reference Lagarias41]. Corollary 2.8 gives the following result on ![]() $\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}$.
Corollary 9.1. Let ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ be such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$ be such that ![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$. Then
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}^{2}$. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\unicode[STIX]{x1D6FE}}{4}+\mathop{\sum }_{n=1}^{\infty }\frac{e^{3n\unicode[STIX]{x1D6FC}/2}}{n(e^{2n\unicode[STIX]{x1D6FC}}-1)}-\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}}{n(e^{4n\unicode[STIX]{x1D6FD}}-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}}{2n-1}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}(2n-1)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}(2n-1)\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad =-\frac{1}{4}\log 2+\frac{\unicode[STIX]{x1D6FC}+8\unicode[STIX]{x1D6FD}}{96}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\unicode[STIX]{x1D6FE}}{4}+\mathop{\sum }_{n=1}^{\infty }\frac{e^{3n\unicode[STIX]{x1D6FC}/2}}{n(e^{2n\unicode[STIX]{x1D6FC}}-1)}-\frac{1}{2}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}}{n(e^{4n\unicode[STIX]{x1D6FD}}-1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }\frac{(-1)^{n}}{2n-1}\biggl(\unicode[STIX]{x1D713}\biggl(\frac{i\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}(2n-1)\biggr)+\unicode[STIX]{x1D713}\biggl(-\frac{i\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70B}}(2n-1)\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad =-\frac{1}{4}\log 2+\frac{\unicode[STIX]{x1D6FC}+8\unicode[STIX]{x1D6FD}}{96}.\end{eqnarray}$$Remark 11. Equation (9.1) implies that if ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ and ![]() $\log 2$ are linearly independent over
$\log 2$ are linearly independent over ![]() $\mathbb{Q}$, then at least one of
$\mathbb{Q}$, then at least one of ![]() $\unicode[STIX]{x1D6FE}$ and the three series on its left-hand side is irrational.
$\unicode[STIX]{x1D6FE}$ and the three series on its left-hand side is irrational.
Corollary 2.11 gives the following two interesting results, one of which involves Catalan’s constant ![]() $G:=\sum _{n=0}^{\infty }(-1)^{n}(2n+1)^{-2}$.
$G:=\sum _{n=0}^{\infty }(-1)^{n}(2n+1)^{-2}$.
Proof. Let ![]() $a=1/2$,
$a=1/2$, ![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}$ in Corollary 2.11 and use the fact [Reference Olver, Lozier, Boisvert and Clark51, page 144, Formula 5.15.3]
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}$ in Corollary 2.11 and use the fact [Reference Olver, Lozier, Boisvert and Clark51, page 144, Formula 5.15.3] ![]() $\unicode[STIX]{x1D713}^{\prime }(1/2)=\unicode[STIX]{x1D70B}^{2}/2$.
$\unicode[STIX]{x1D713}^{\prime }(1/2)=\unicode[STIX]{x1D70B}^{2}/2$.
Note that (9.2) is an analogue of the following famous result, first proved by Schlömilch [Reference Schlömilch58] (see [Reference Berndt7, page 159] for more references):
Corollary 9.3. If ![]() $G$ denotes Catalan’s constant, then
$G$ denotes Catalan’s constant, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{ne^{\frac{3n\unicode[STIX]{x1D70B}}{2}}}{e^{2n\unicode[STIX]{x1D70B}}-1}+2\mathop{\sum }_{n=1}^{\infty }\frac{n(-1)^{n}}{e^{4n\unicode[STIX]{x1D70B}}-1}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2G}{\unicode[STIX]{x1D70B}^{2}}+\frac{1}{4}\biggl(1-\frac{1}{\unicode[STIX]{x1D70B}}\biggr)+\frac{1}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }(-1)^{n-1}(2n-1)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\log (2n-1)-\frac{1}{2}(\unicode[STIX]{x1D713}(i(2n-1))+\unicode[STIX]{x1D713}(-i(2n-1)))\bigg\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{ne^{\frac{3n\unicode[STIX]{x1D70B}}{2}}}{e^{2n\unicode[STIX]{x1D70B}}-1}+2\mathop{\sum }_{n=1}^{\infty }\frac{n(-1)^{n}}{e^{4n\unicode[STIX]{x1D70B}}-1}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2G}{\unicode[STIX]{x1D70B}^{2}}+\frac{1}{4}\biggl(1-\frac{1}{\unicode[STIX]{x1D70B}}\biggr)+\frac{1}{\unicode[STIX]{x1D70B}}\mathop{\sum }_{n=1}^{\infty }(-1)^{n-1}(2n-1)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg\{\log (2n-1)-\frac{1}{2}(\unicode[STIX]{x1D713}(i(2n-1))+\unicode[STIX]{x1D713}(-i(2n-1)))\bigg\}.\nonumber\end{eqnarray}$$Proof. Let ![]() $a=1/4,\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}$ in Corollary 2.11 and use the fact [Reference Olver, Lozier, Boisvert and Clark51, page 144, Formula 5.15.1]
$a=1/4,\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70B}$ in Corollary 2.11 and use the fact [Reference Olver, Lozier, Boisvert and Clark51, page 144, Formula 5.15.1] ![]() $\unicode[STIX]{x1D713}^{\prime }(1/4)=8G+\unicode[STIX]{x1D70B}^{2}$.
$\unicode[STIX]{x1D713}^{\prime }(1/4)=8G+\unicode[STIX]{x1D70B}^{2}$.
10 Concluding remarks
All of our results involving ![]() $x$, or
$x$, or ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FD}$, can be extended by analytic continuation to complex values of
$\unicode[STIX]{x1D6FD}$, can be extended by analytic continuation to complex values of ![]() $x,\unicode[STIX]{x1D6FC}$, and
$x,\unicode[STIX]{x1D6FC}$, and ![]() $\unicode[STIX]{x1D6FD}$ such that
$\unicode[STIX]{x1D6FD}$ such that ![]() $\text{Re}(x)>0$,
$\text{Re}(x)>0$, ![]() $\text{Re}(\unicode[STIX]{x1D6FC})>0$ and
$\text{Re}(\unicode[STIX]{x1D6FC})>0$ and ![]() $\text{Re}(\unicode[STIX]{x1D6FD})>0$.
$\text{Re}(\unicode[STIX]{x1D6FD})>0$.
We note that Theorems 2.6 and 2.12 lead to Zudilin-type results on transcendence similar to the ones obtained in [Reference Dixit and Maji21]. This, as well as Remark 11, suggests that in order to understand the arithmetical nature of Euler’s constant, the values of the Riemann zeta function at odd positive integers as well as at rational arguments, further study of the generalized Lambert series considered here seems to be essential. There have been many studies on irrationality of certain Lambert series, for example, by Erdös [Reference Erdös25] and by Luca and Tachiya [Reference Luca and Tachiya45]. We refer the reader to two recent papers [Reference Boxall and Jones14, Reference Masser47] for some quantitative results on rational values of the Riemann zeta function.
When ![]() $N\in 2\mathbb{N}$, we were able to transform the series
$N\in 2\mathbb{N}$, we were able to transform the series ![]() $\sum _{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}$,
$\sum _{n=1}^{\infty }n^{N-2h}\frac{\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)}$, ![]() $0<a\leqslant 1$, for any integer
$0<a\leqslant 1$, for any integer ![]() $h$. However, for
$h$. However, for ![]() $N$ odd and positive, we could do so only for
$N$ odd and positive, we could do so only for ![]() $h\geqslant 0$. Thus it remains to be seen if there exists a transformation of this series when
$h\geqslant 0$. Thus it remains to be seen if there exists a transformation of this series when ![]() $N$ is odd and
$N$ is odd and ![]() $h<0$. If done, this might give us a complete generalization of (1.2), that is of [Reference Dixit and Maji21, Theorem 1.2].
$h<0$. If done, this might give us a complete generalization of (1.2), that is of [Reference Dixit and Maji21, Theorem 1.2].
Our Theorems 2.1 and 2.10 can be conceived of as formulas for the Hurwitz zeta function at rational arguments, namely ![]() $\unicode[STIX]{x1D701}(\frac{b}{c},a)$, when
$\unicode[STIX]{x1D701}(\frac{b}{c},a)$, when ![]() $b$ is odd and
$b$ is odd and ![]() $c$ is a positive even integer, or when
$c$ is a positive even integer, or when ![]() $b$ is even and
$b$ is even and ![]() $c$ is a positive odd integer. The only other case which remains to be seen is when
$c$ is a positive odd integer. The only other case which remains to be seen is when ![]() $b$ and
$b$ and ![]() $c$ are both odd since the case when they are both even can be reduced to one of the three cases.
$c$ are both odd since the case when they are both even can be reduced to one of the three cases.
Let ![]() $\unicode[STIX]{x1D712}$ denote the primitive Dirichlet character modulo
$\unicode[STIX]{x1D712}$ denote the primitive Dirichlet character modulo ![]() $q$. Using the identity [Reference Davenport18, page 71, Equation (16)]
$q$. Using the identity [Reference Davenport18, page 71, Equation (16)] ![]() $L(s,\unicode[STIX]{x1D712})=q^{-s}\sum _{n=1}^{q}\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D701}(s,n/q)$ and Theorem 2.1, we can obtain a representation for
$L(s,\unicode[STIX]{x1D712})=q^{-s}\sum _{n=1}^{q}\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D701}(s,n/q)$ and Theorem 2.1, we can obtain a representation for ![]() $L(\frac{N-2h+1}{N},\unicode[STIX]{x1D712})$. This representation may be useful in its numerical computation. In [Reference Dixit and Maji21], it was shown that any two odd zeta values of the form
$L(\frac{N-2h+1}{N},\unicode[STIX]{x1D712})$. This representation may be useful in its numerical computation. In [Reference Dixit and Maji21], it was shown that any two odd zeta values of the form ![]() $\unicode[STIX]{x1D701}(4k+3)$ are related to each other by means of the relation that each such odd zeta value obeys with
$\unicode[STIX]{x1D701}(4k+3)$ are related to each other by means of the relation that each such odd zeta value obeys with ![]() $\unicode[STIX]{x1D701}(3)$ as governed by the case
$\unicode[STIX]{x1D701}(3)$ as governed by the case ![]() $a=1$ of Theorem 2.4, that is, (1.2). Also, while it was shown that such a relation is not possible for every pair of the form
$a=1$ of Theorem 2.4, that is, (1.2). Also, while it was shown that such a relation is not possible for every pair of the form ![]() $(\unicode[STIX]{x1D701}(4k_{1}+1),\unicode[STIX]{x1D701}(4k_{2}+1))$, through (1.2), it does exist for some such pairs. However, (1.2) has a limitation in that no two odd zeta values, one of which is of the form
$(\unicode[STIX]{x1D701}(4k_{1}+1),\unicode[STIX]{x1D701}(4k_{2}+1))$, through (1.2), it does exist for some such pairs. However, (1.2) has a limitation in that no two odd zeta values, one of which is of the form ![]() $\unicode[STIX]{x1D701}(4k_{1}+1)$ and another
$\unicode[STIX]{x1D701}(4k_{1}+1)$ and another ![]() $\unicode[STIX]{x1D701}(4k_{2}+3)$, are related through it. This is partially overcome through our generalization of (1.2), that is, Theorem 2.4, in that now it is possible to have a relation between two odd zeta values, one of the form
$\unicode[STIX]{x1D701}(4k_{2}+3)$, are related through it. This is partially overcome through our generalization of (1.2), that is, Theorem 2.4, in that now it is possible to have a relation between two odd zeta values, one of the form ![]() $\unicode[STIX]{x1D701}(4k+3)$ and another of the form
$\unicode[STIX]{x1D701}(4k+3)$ and another of the form ![]() $\unicode[STIX]{x1D701}(8k+5)$. (To see this, let
$\unicode[STIX]{x1D701}(8k+5)$. (To see this, let ![]() $m=2$ and
$m=2$ and ![]() $0<a<1,a\neq \frac{1}{2}$, in Theorem 2.4.) This prompts to ask if there exists a transformation which would relate two odd zeta values, one of the form
$0<a<1,a\neq \frac{1}{2}$, in Theorem 2.4.) This prompts to ask if there exists a transformation which would relate two odd zeta values, one of the form ![]() $\unicode[STIX]{x1D701}(4k+3)$ and another,
$\unicode[STIX]{x1D701}(4k+3)$ and another, ![]() $\unicode[STIX]{x1D701}(8k+1)$.
$\unicode[STIX]{x1D701}(8k+1)$.
Gun et al. [Reference Gun, Murty and Rath32] have defined Ramanujan polynomials by
These are reciprocal polynomials which occur on the right-hand side of (1.1) and satisfy many interesting properties, for example, all nonreal zeros of these polynomials lie on the unit circle [Reference Murty, Smyth and Wang48]. It may be worthwhile to investigate the properties of the generalized Ramanujan polynomials that turn up in our Theorem 2.4 which are different from the generalized Ramanujan polynomials considered in [Reference Berndt and Straub12, Equation (43)].
Acknowledgments
The authors sincerely thank the referee for his/her useful suggestions. They also thank Ram Murty, Yuri V. Nesterenko, Purusottam Rath, Michel Waldschmidt and Wadim Zudilin for interesting discussions. The first author’s research is supported by SERB-DST grant ECR/2015/000070, whereas the third author is a SERB National Post Doctoral Fellow (NPDF) supported by the fellowship PDF/2017/000370. Both sincerely thank SERB-DST for the support.