Refine listing
Actions for selected content:
236 results in 11Jxx
ON THE DIOPHANTINE PROPERTIES OF λ-EXPANSIONS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 65-86
- Print publication:
- January 2013
-
- Article
- Export citation
APPROXIMATION OF AN ALGEBRAIC NUMBER BY PRODUCTS OF RATIONAL NUMBERS AND UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 121-131
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
CONTINUED FRACTIONS FOR A CLASS OF TRIANGLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 21-42
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON MAHLER’S
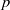 $p$-ADIC
$p$-ADIC 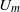 $U_{m}$-NUMBERS
$U_{m}$-NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 21 August 2012, pp. 44-50
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
ON MULTIPLICATIVELY BADLY APPROXIMABLE NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 31-55
- Print publication:
- January 2013
-
- Article
- Export citation
SOME EXACT ALGEBRAIC EXPRESSIONS FOR THE TAILS OF TASOEV CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 179-193
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
IRRATIONALITY AND NONQUADRATICITY MEASURES FOR LOGARITHMS OF ALGEBRAIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 237-267
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Continued fractions with low complexity: transcendence measures and quadratic approximation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 718-750
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
On the convergence of Diophantine Dirichlet series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 513-541
-
- Article
-
- You have access
- Export citation
RATIONAL APPROXIMATIONS TO VALUES OF BELL POLYNOMIALS AT POINTS INVOLVING EULER’S CONSTANT AND ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 71-98
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
VARIATIONS AROUND A PROBLEM OF MAHLER AND MENDÈS FRANCE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 25 April 2012, pp. 37-44
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
On simultaneous rational approximation to a p-adic number and its integral powers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 17 August 2011, pp. 599-612
-
- Article
-
- You have access
- Export citation
ERDŐS’ METHOD FOR DETERMINING THE IRRATIONALITY OF PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 13 July 2011, pp. 414-424
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON BADLY APPROXIMABLE LINEAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 04 February 2011, pp. 262-266
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
DISTANCE BETWEEN ARITHMETIC PROGRESSIONS AND PERFECT SQUARES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 41-49
- Print publication:
- January 2011
-
- Article
- Export citation
ALGEBRAIC VALUES OF TRANSCENDENTAL FUNCTIONS AT ALGEBRAIC POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 322-327
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
The distribution of close conjugate algebraic numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 1165-1179
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
ON SHRINKING TARGETS FOR ℤm ACTIONS ON TORI
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 16 April 2010, pp. 193-202
- Print publication:
- July 2010
-
- Article
- Export citation
SIMULTANEOUS DIOPHANTINE APPROXIMATION ON POLYNOMIAL CURVES
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 77-85
- Print publication:
- January 2010
-
- Article
- Export citation
Spectral numbers in Floer theories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1581-1592
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
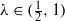 and
and 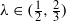 , the upper bound of
, the upper bound of 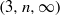
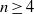
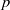
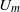
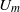
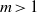
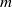
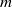
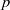
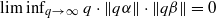 for all (
for all (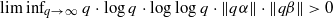 is of full dimension.
is of full dimension.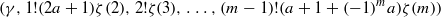
 can be the exceptional set of some transcendental entire function. Furthermore, we give a much more general version of this theorem and present a unified proof.
can be the exceptional set of some transcendental entire function. Furthermore, we give a much more general version of this theorem and present a unified proof.