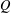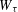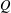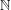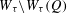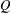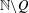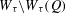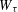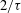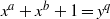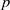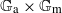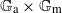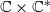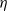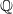Refine listing
Actions for selected content:
236 results in 11Jxx
THE DUFFIN–SCHAEFFER-TYPE CONJECTURES IN VARIOUS LOCAL FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 06 May 2016, pp. 753-800
- Print publication:
- 2016
-
- Article
- Export citation
A DICHOTOMY LAW FOR THE DIOPHANTINE PROPERTIES IN
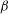 $\unicode[STIX]{x1D6FD}$ -DYNAMICAL SYSTEMS
$\unicode[STIX]{x1D6FD}$ -DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 884-897
- Print publication:
- 2016
-
- Article
- Export citation
Rational Values of Weierstrass Zeta Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 945-958
-
- Article
- Export citation
Arithmetic Density
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 14 December 2015, pp. 691-700
-
- Article
- Export citation
ON A PROBLEM POSED BY MAHLER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 86-107
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
A NOTE ON LACUNARY POWER SERIES WITH RATIONAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 372-374
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
An explicit Baker-type lower bound of exponential values
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 27 October 2015, pp. 1153-1182
- Print publication:
- December 2015
-
- Article
- Export citation
ON THE SPECTRUM OF DIOPHANTINE APPROXIMATION CONSTANTS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 June 2015, pp. 79-100
- Print publication:
- 2016
-
- Article
- Export citation
On the complexity of a putative counterexample to the
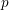 $p$-adic Littlewood conjecture
$p$-adic Littlewood conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 19 May 2015, pp. 1647-1662
- Print publication:
- September 2015
-
- Article
- Export citation
ALGEBRAIC INDEPENDENCE OF CERTAIN MAHLER FUNCTIONS AND OF THEIR VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 289-310
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
A Frostman-Type Lemma for Sets with Large Intersections, and an Application to Diophantine Approximation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 521-542
-
- Article
-
- You have access
- Export citation
HAUSDORFF DIMENSIONS OF SOME LIMINF SETS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 101-120
- Print publication:
- January 2015
-
- Article
- Export citation
Linear independence of monomials of multizeta values in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1789-1808
- Print publication:
- November 2014
-
- Article
- Export citation
Class numbers of real cyclotomic fields of composite conductor
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 404-417
-
- Article
-
- You have access
- Export citation
ON A VARIANT OF A QUESTION PROPOSED BY K. MAHLER CONCERNING LIOUVILLE NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 09 July 2014, pp. 29-33
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
PERFECT POWERS WITH THREE DIGITS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 66-84
- Print publication:
- January 2014
-
- Article
- Export citation
A SMALL VALUE ESTIMATE FOR
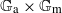 $\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$
$\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 01 February 2013, pp. 333-363
- Print publication:
- July 2013
-
- Article
- Export citation
ZERO-ONE LAWS IN SIMULTANEOUS AND MULTIPLICATIVE DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 21 January 2013, pp. 321-332
- Print publication:
- July 2013
-
- Article
- Export citation
ON A SEQUENCE INVOLVING SUMS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 197-205
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
A NOTE ON THE HAUSDORFF DIMENSION OF SOME LIMINF SETS APPEARING IN SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 56-64
- Print publication:
- January 2013
-
- Article
- Export citation
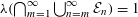
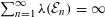

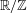
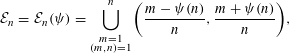
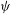
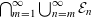
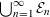

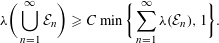
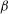
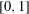
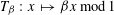
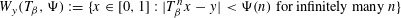
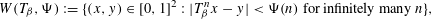
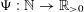

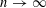
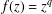
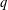
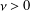
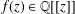
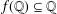
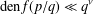
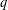
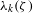
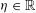
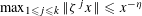


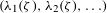
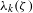
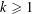
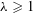
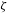
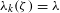
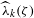
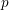

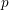
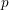
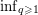

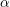
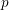
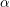
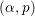
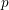
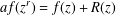


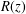
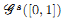 of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least
of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least 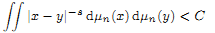
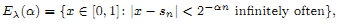
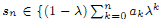 and
and 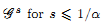 . This improves one of our previously published results.
. This improves one of our previously published results.