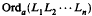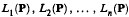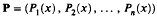Refine listing
Actions for selected content:
240 results in 11Jxx
Legendre transforms and Apéry's sequences
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 358-375
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
A note on Beukers' integral
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-153
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
The Hausdorff dimension of systems of simultaneously small linear forms
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 367-374
- Print publication:
- December 1993
-
- Article
- Export citation
On the frequency distribution of partial quotients of U-numbers
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-225
- Print publication:
- December 1993
-
- Article
- Export citation
On Mahler's compound bodies
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-215
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
Multiple Franel integrals
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-70
- Print publication:
- June 1993
-
- Article
- Export citation
Geometric and arithmetic postulation of the exponential function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-127
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
A problem of Good on Hausdorff dimension
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 244-246
- Print publication:
- December 1992
-
- Article
- Export citation
Metrical properties of best approximants
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-91
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
T-numbers form an M0 set
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-24
- Print publication:
- June 1992
-
- Article
- Export citation
An improvement of a transcendence measure of Galochkin and Mahler's S-numbers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 130-140
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
Large transcendence degree
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 3 / December 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 400-422
- Print publication:
- December 1991
-
- Article
-
- You have access
- Export citation
Diophantine approximation by continued fractions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 324-330
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
Generalised simultaneous approximation of functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 50-61
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Additive relations in fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 154-170
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Optimal approximation by continued fractions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 481-504
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
A note on asymmetric approximation
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 34-41
- Print publication:
- June 1991
-
- Article
- Export citation
On the distribution of apk modulo one
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-184
- Print publication:
- June 1991
-
- Article
- Export citation
A subspace theorem for ordinary linear differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 320-332
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Some quantitative results related to Roth's Theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-248
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
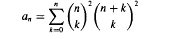
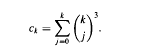
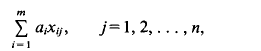

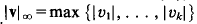 of any vector in
of any vector in 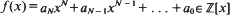 so that
so that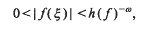

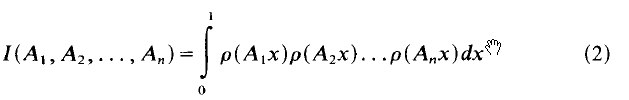
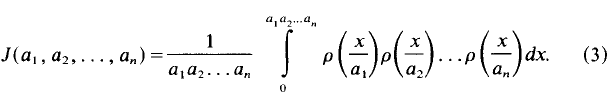
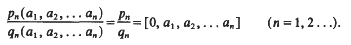
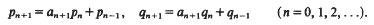
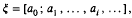
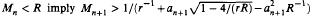 which generalizes a previous result of the author.
which generalizes a previous result of the author.