Refine listing
Actions for selected content:
237 results in 11Jxx
Spectral numbers in Floer theories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1581-1592
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
APPROXIMATION BY SEVERAL RATIONALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 325-329
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
A Groshev Theorem for Small Linear Forms
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 79-85
- Print publication:
- December 2005
-
- Article
- Export citation
Pseudo-elliptic integrals, units, and torsion
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-347
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
The unreasonable effectualness of continued function expansions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-320
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Parametrizing simple closed geodesy on Γ3\ℋ
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 43-60
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Irrational dilations of Pascal's triangle
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-168
- Print publication:
- December 2001
-
- Article
- Export citation
Fractional parts of Linear polynomials and an application to hypergeometric functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-424
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Independance algebrique des derivees d'une periode du module de Carlitz
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-18
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Effective measures of irrationality for certain algebraic numbers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-344
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Appendix to the paper by T. Łuczak—A simple proof of the lower
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 54-55
- Print publication:
- June 1997
-
- Article
- Export citation
On the fractional dimension of sets of continued fractions
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-53
- Print publication:
- June 1997
-
- Article
- Export citation
A note on metric inhomogeneous Diophantine approximation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-185
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
Hall's ray in inhomogeneous diophantine approximation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 42-50
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Reconstructing curves from sets of quantized observations
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 340-353
- Print publication:
- December 1995
-
- Article
- Export citation
The number of exceptional approximations in Roth's theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 375-383
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
The continuous Diophantine approximation mapping of Szekeres
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 148-172
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Legendre transforms and Apéry's sequences
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 358-375
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
A note on Beukers' integral
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-153
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
The Hausdorff dimension of systems of simultaneously small linear forms
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 367-374
- Print publication:
- December 1993
-
- Article
- Export citation
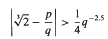 for any non-zero integers
for any non-zero integers 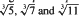 . Some Diophantine consequences are briefly discussed.
. Some Diophantine consequences are briefly discussed. (
(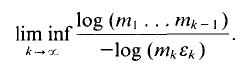
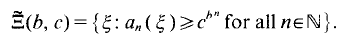
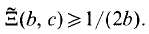 On the other hand, Moorthy [8] showed that dim
On the other hand, Moorthy [8] showed that dim 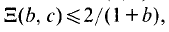 where
where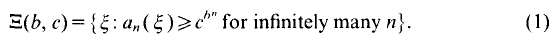
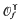 of
of 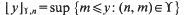
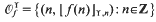
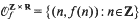 and
and 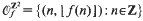 , where [x] (without subscript) denotes as usual the integer part of
, where [x] (without subscript) denotes as usual the integer part of 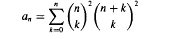
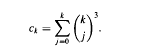
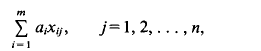

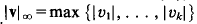 of any vector in
of any vector in 