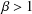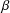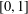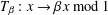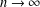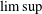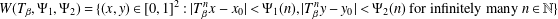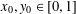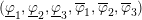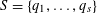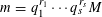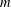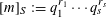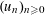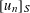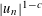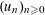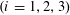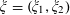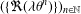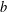Refine listing
Actions for selected content:
236 results in 11Jxx
TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 33-42
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
On the topology of Diophantine approximation spectra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1512-1546
- Print publication:
- July 2017
-
- Article
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation
TRANSCENDENCE OVER MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 393-399
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Picard curves over
 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 382-408
-
- Article
-
- You have access
- Export citation
PARAMETRIC GEOMETRY OF NUMBERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1114-1135
- Print publication:
- 2017
-
- Article
- Export citation
FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 715-733
- Print publication:
- 2017
-
- Article
- Export citation
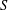 $S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
$S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 840-851
- Print publication:
- 2017
-
- Article
- Export citation
A NOTE ON BADLY APPROXIMABLE LINEAR FORMS ON MANIFOLDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 11 May 2017, pp. 587-601
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
SIMULTANEOUS APPROXIMATION TO TWO REALS: BOUNDS FOR THE SECOND SUCCESSIVE MINIMUM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1136-1151
- Print publication:
- 2017
-
- Article
- Export citation
INTRINSIC DIOPHANTINE APPROXIMATION ON GENERAL POLYNOMIAL SURFACES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 250-259
- Print publication:
- 2017
-
- Article
- Export citation
ON A PROBLEM OF ERDÖS AND MAHLER CONCERNING CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 183-186
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
AN UPPER BOUND FOR THE NUMBER OF DIOPHANTINE QUINTUPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 384-394
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
RESTRICTED SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 34-52
- Print publication:
- 2017
-
- Article
- Export citation
A NOTE ON WEIGHTED BADLY APPROXIMABLE LINEAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 349-357
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
ON EXCEPTIONAL SETS: THE SOLUTION OF A PROBLEM POSED BY K. MAHLER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 15-19
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
ON REAL PARTS OF POWERS OF COMPLEX PISOT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 245-253
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ABSOLUTELY ABNORMAL AND CONTINUED FRACTION NORMAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 217-223
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Relative Manin–Mumford for Semi-Abelian Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 18 January 2016, pp. 837-875
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 375-387
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation