Hostname: page-component-cb9f654ff-5jtmz Total loading time: 0 Render date: 2025-08-15T14:28:04.983Z Has data issue: false hasContentIssue false
  • English
  • Français

SIMULTANEOUS APPROXIMATION TO TWO REALS: BOUNDS FOR THE SECOND SUCCESSIVE MINIMUM

Part of: Geometry of numbers Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  29 November 2017

Wolfgang M. Schmidt  and
Leonhard Summerer
Wolfgang M. Schmidt
Affiliation:
Department of Mathematics, University of Colorado, Boulder, CO 80309-0395, U.S.A. email wolfgang.schmidt@colorado.edu
Leonhard Summerer
Affiliation:
Fakultät für Mathematik der Universität Wien, Oskar-Morgenstern-Platz 1, 1090 Wien, Austria email leonhard.summerer@univie.ac.at
Get access

Abstract

Introduced in Schmidt and Summerer [Parametric geometry of numbers and applications. Acta Arith.140 (2009), 67–91], approximation exponents 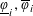$\text{}\underline{\unicode[STIX]{x1D711}}_{i},\overline{\unicode[STIX]{x1D711}}_{i}$ , 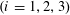$(i=1,2,3)$ , attached to points 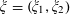$\boldsymbol{\unicode[STIX]{x1D709}}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})$ in 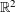$\mathbb{R}^{2}$ , give information on Diophantine approximation properties of these points. Laurent [Exponents of Diophantine approximation in dimension two. Canad. J. Math.61 (2009), 165–189] had described all possible quadruples 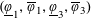$(\text{}\underline{\unicode[STIX]{x1D711}}_{1},\overline{\unicode[STIX]{x1D711}}_{1},\text{}\underline{\unicode[STIX]{x1D711}}_{3},\overline{\unicode[STIX]{x1D711}}_{3})$ arising in this way. Our emphasis here will be on 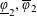$\text{}\underline{\unicode[STIX]{x1D711}}_{2},\overline{\unicode[STIX]{x1D711}}_{2}$ and the construction of suitable “ 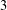$3$ -systems”.

MSC classification

Primary: 11H06: Lattices and convex bodies 11J13: Simultaneous homogeneous approximation, linear forms

Information

Type
Research Article
Information
Mathematika , Volume 63 , Issue 3 , 2017 , pp. 1136 - 1151
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Laurent, M., Exponents of Diophantine approximation in dimension two. Canad. J. Math. 61 2009, 165–189.Google Scholar
Roy, D., On Schmidt and Summerer parametric geometry of numbers. Ann. of Math. (2) 182 2015, 739–786.Google Scholar
Roy, D., On the topology of Diophantine approximation spectra. Compos. Math. 153 2017, 1512–1546.CrossRefGoogle Scholar
Schmidt, W. M. and Summerer, L., Parametric geometry of numbers and applications. Acta Arith. 140 2009, 67–91.CrossRefGoogle Scholar
Schmidt, W. M. and Summerer, L., Diophantine approximation and parametric geometry of numbers. Monatsh. Math. 169 2013, 51–104.Google Scholar
Schmidt, W. M. and Summerer, L., The generalization of Jarnik’s identity. Acta Arith. 175 2016, 119–136.Google Scholar