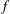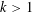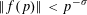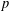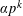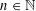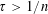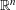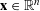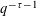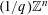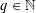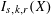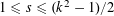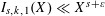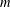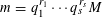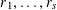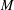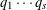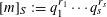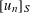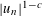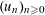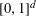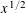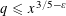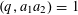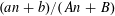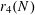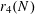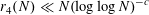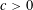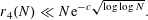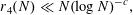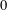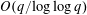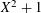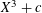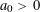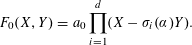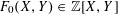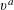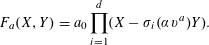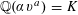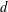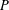Contents
Editorial
IN MEMORIAM KLAUS FRIEDRICH ROTH 1925–2015
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 711-712
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
ABCOLOGICAL ANECDOTES
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 713-714
-
- Article
- Export citation
FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 715-733
-
- Article
- Export citation
DIMENSION-FREE UNIFORMITY WITH APPLICATIONS, I
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 734-761
-
- Article
-
- You have access
- HTML
- Export citation
DIOPHANTINE APPROXIMATION ON MANIFOLDS AND LOWER BOUNDS FOR HAUSDORFF DIMENSION
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 762-779
-
- Article
- Export citation
RATIONAL POINTS ON THE INNER PRODUCT CONE VIA THE HYPERBOLA METHOD
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 780-796
-
- Article
- Export citation
VINOGRADOV SYSTEMS WITH A SLICE OFF
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 797-817
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MANY CUBIC SURFACES CONTAIN RATIONAL POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 818-839
-
- Article
- Export citation
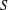 $S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
$S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 840-851
-
- Article
- Export citation
PRIME NUMBER THEOREM EQUIVALENCES AND NON-EQUIVALENCES
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 852-862
-
- Article
- Export citation
DISCREPANCY OF SECOND ORDER DIGITAL SEQUENCES IN FUNCTION SPACES WITH DOMINATING MIXED SMOOTHNESS
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 863-894
-
- Article
- Export citation
SMOOTH-SUPPORTED MULTIPLICATIVE FUNCTIONS IN ARITHMETIC PROGRESSIONS BEYOND THE
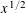 $x^{1/2}$ -BARRIER
$x^{1/2}$ -BARRIER
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 895-918
-
- Article
- Export citation
HARMONIC ANALYSIS ON THE POSITIVE RATIONALS. DETERMINATION OF THE GROUP GENERATED BY THE RATIOS
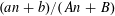 $(an+b)/(An+B)$
$(an+b)/(An+B)$
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 919-943
-
- Article
- Export citation
NEW BOUNDS FOR SZEMERÉDI’S THEOREM, III: A POLYLOGARITHMIC BOUND FOR
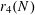 $r_{4}(N)$
$r_{4}(N)$
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 944-1040
-
- Article
-
- You have access
- HTML
- Export citation
ITERATION OF QUADRATIC POLYNOMIALS OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1041-1059
-
- Article
- Export citation
FAMILIES OF THUE EQUATIONS ASSOCIATED WITH A RANK ONE SUBGROUP OF THE UNIT GROUP OF A NUMBER FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1060-1080
-
- Article
- Export citation
ON MULTIPLICATIVE COMPOSITIONS OF INTEGERS
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1081-1090
-
- Article
- Export citation
TIGHTER BOUNDS FOR THE DISCREPANCY OF BOXESAND POLYTOPES
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1091-1113
-
- Article
- Export citation
PARAMETRIC GEOMETRY OF NUMBERS IN FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1114-1135
-
- Article
- Export citation
SIMULTANEOUS APPROXIMATION TO TWO REALS: BOUNDS FOR THE SECOND SUCCESSIVE MINIMUM
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1136-1151
-
- Article
- Export citation