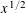Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shparlinski, Igor E.
2018.
Character sums with smooth numbers.
Archiv der Mathematik,
Vol. 110,
Issue. 5,
p.
467.
GRANVILLE, ANDREW
and
SHAO, XUANCHENG
2018.
WHEN DOES THE BOMBIERI–VINOGRADOV THEOREM HOLD FOR A GIVEN MULTIPLICATIVE FUNCTION?.
Forum of Mathematics, Sigma,
Vol. 6,
Issue. ,
Granville, Andrew
and
Shao, Xuancheng
2019.
Bombieri-Vinogradov for multiplicative functions, and beyond the x1/2-barrier.
Advances in Mathematics,
Vol. 350,
Issue. ,
p.
304.
Roy, Arindam
and
Vatwani, Akshaa
2020.
Zeros of Dirichlet polynomials.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 1,
p.
643.
Savalia, Aditi
and
Vatwani, Akshaa
2023.
Limitations to equidistribution in arithmetic progressions.
Research in the Mathematical Sciences,
Vol. 10,
Issue. 1,
Klurman, Oleksiy
Mangerel, Alexander P.
and
Teräväinen, Joni
2023.
Multiplicative functions in short arithmetic progressions.
Proceedings of the London Mathematical Society,
Vol. 127,
Issue. 2,
p.
366.
Pascadi, Alexandru
2025.
Smooth numbers in arithmetic progressions to large moduli.
Compositio Mathematica,
Vol. 161,
Issue. 8,
p.
1923.