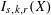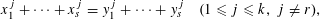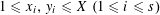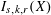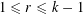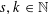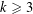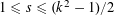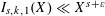1 Introduction
Systems of symmetric diagonal equations are, by orthogonality, intimately connected with mean values of exponential sums, and consequently find numerous applications in the analytic theory of numbers. In this paper we consider the number
![]() $I_{s,k,r}(X)$
of integral solutions of the system of equations
$I_{s,k,r}(X)$
of integral solutions of the system of equations
with
![]() $1\leqslant x_{i},y_{i}\leqslant X\;(1\leqslant i\leqslant s)$
. This system is related to that of Vinogradov in which the equations (1.1) are augmented with the additional slice
$1\leqslant x_{i},y_{i}\leqslant X\;(1\leqslant i\leqslant s)$
. This system is related to that of Vinogradov in which the equations (1.1) are augmented with the additional slice
and may be viewed as a testing ground for progress on systems not of Vinogradov type. Relatives of such systems have been employed in work on the existence of rational points on systems of diagonal hypersurfaces as well as cognate paucity problems (see for example [Reference Brandes and Parsell2–Reference Brüdern and Robert4]). The main conjecture for the system (1.1) asserts that whenever
![]() $r,s,k\in \mathbb{N}$
,
$r,s,k\in \mathbb{N}$
,
![]() $r<k$
and
$r<k$
and
![]() $\unicode[STIX]{x1D700}>0$
, then
$\unicode[STIX]{x1D700}>0$
, then
Here and throughout, the constants implicit in Vinogradov’s notation may depend on
![]() $s$
,
$s$
,
![]() $k$
, and
$k$
, and
![]() $\unicode[STIX]{x1D700}$
. It is an easy exercise to establish a lower bound for
$\unicode[STIX]{x1D700}$
. It is an easy exercise to establish a lower bound for
![]() $I_{s,k,r}(X)$
that shows the estimate (1.2) to be best possible, save that when
$I_{s,k,r}(X)$
that shows the estimate (1.2) to be best possible, save that when
![]() $k>2$
one may expect to be able to take
$k>2$
one may expect to be able to take
![]() $\unicode[STIX]{x1D700}$
to be zero. Our focus in this memoir is the diagonal regime
$\unicode[STIX]{x1D700}$
to be zero. Our focus in this memoir is the diagonal regime
![]() $I_{s,k,r}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
, and this we address with some level of success in the case
$I_{s,k,r}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
, and this we address with some level of success in the case
![]() $r=1$
.
$r=1$
.
Theorem 1.1. Let
![]() $s,k\in \mathbb{N}$
satisfy
$s,k\in \mathbb{N}$
satisfy
![]() $k\geqslant 3$
and
$k\geqslant 3$
and
![]() $1\leqslant s\leqslant (k^{2}-1)/2$
. Then for each
$1\leqslant s\leqslant (k^{2}-1)/2$
. Then for each
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
![]() $I_{s,k,1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
$I_{s,k,1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
In view of the main conjecture (1.2), one would expect the conclusion of Theorem 1.1 to hold in the extended range
![]() $1\leqslant s\leqslant (k^{2}+k-2)/2$
. Previous work already in the literature falls far short of such ambitious assertions. Work of the second author from the early 1990s shows that
$1\leqslant s\leqslant (k^{2}+k-2)/2$
. Previous work already in the literature falls far short of such ambitious assertions. Work of the second author from the early 1990s shows that
![]() $I_{s,k,r}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
only for
$I_{s,k,r}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
only for
![]() $1\leqslant s\leqslant k$
(see [Reference Wooley, Pollington and Moran7, Theorem 1]). Meanwhile, as a consequence of the second author’s resolution of the main conjecture in the cubic case of Vinogradov’s mean value theorem [Reference Wooley9, Theorem 1.1], one has the bound
$1\leqslant s\leqslant k$
(see [Reference Wooley, Pollington and Moran7, Theorem 1]). Meanwhile, as a consequence of the second author’s resolution of the main conjecture in the cubic case of Vinogradov’s mean value theorem [Reference Wooley9, Theorem 1.1], one has the bound
![]() $I_{s,3,1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
for
$I_{s,3,1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
for
![]() $1\leqslant s\leqslant 4$
(see [Reference Wooley8, Theorem 1.3]). This conclusion is matched by that of Theorem 1.1 above in the special case
$1\leqslant s\leqslant 4$
(see [Reference Wooley8, Theorem 1.3]). This conclusion is matched by that of Theorem 1.1 above in the special case
![]() $k=3$
. The ideas underlying recent progress on Vinogradov’s mean value theorem can, however, be brought to bear on the problem of estimating
$k=3$
. The ideas underlying recent progress on Vinogradov’s mean value theorem can, however, be brought to bear on the problem of estimating
![]() $I_{s,k,r}(X)$
. Thus, it is a consequence of the second author’s work on nested efficient congruencing [Reference Wooley10, Corollary 1.2] that one has
$I_{s,k,r}(X)$
. Thus, it is a consequence of the second author’s work on nested efficient congruencing [Reference Wooley10, Corollary 1.2] that one has
![]() $I_{s,k,r}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
for
$I_{s,k,r}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
for
![]() $1\leqslant s\leqslant k(k-1)/2$
. Such a conclusion could also be established through methods related to those of Bourgain, Demeter and Guth [Reference Bourgain, Demeter and Guth1], though the necessary details have yet to be elucidated in the published literature. Both the aforementioned estimate
$1\leqslant s\leqslant k(k-1)/2$
. Such a conclusion could also be established through methods related to those of Bourgain, Demeter and Guth [Reference Bourgain, Demeter and Guth1], though the necessary details have yet to be elucidated in the published literature. Both the aforementioned estimate
![]() $I_{4,3,1}(X)\ll X^{4+\unicode[STIX]{x1D700}}$
, and the new bound reported in Theorem 1.1 go well beyond this work based on efficient congruencing and
$I_{4,3,1}(X)\ll X^{4+\unicode[STIX]{x1D700}}$
, and the new bound reported in Theorem 1.1 go well beyond this work based on efficient congruencing and
![]() $l^{2}$
-decoupling. Indeed, when
$l^{2}$
-decoupling. Indeed, when
![]() $r=1$
we achieve an estimate tantamount to square-root cancellation in a range of
$r=1$
we achieve an estimate tantamount to square-root cancellation in a range of
![]() $2s$
-th moments extending the interval
$2s$
-th moments extending the interval
![]() $1\leqslant s\leqslant k(k-1)/2$
roughly half way to the full conjectured range
$1\leqslant s\leqslant k(k-1)/2$
roughly half way to the full conjectured range
![]() $1\leqslant s\leqslant (k^{2}+k-2)/2$
.
$1\leqslant s\leqslant (k^{2}+k-2)/2$
.
Our strategy for proving Theorem 1.1 is based on the proof of the estimate
![]() $I_{4,3,1}(X)\ll X^{4+\unicode[STIX]{x1D700}}$
in [Reference Wooley8, Theorem 1.3], though it is flexible enough to deliver estimates for the mean value
$I_{4,3,1}(X)\ll X^{4+\unicode[STIX]{x1D700}}$
in [Reference Wooley8, Theorem 1.3], though it is flexible enough to deliver estimates for the mean value
![]() $I_{s,k,r}(X)$
with
$I_{s,k,r}(X)$
with
![]() $r\geqslant 1$
, as we now outline. For each integral solution
$r\geqslant 1$
, as we now outline. For each integral solution
![]() $\mathbf{x},\mathbf{y}$
of the system (1.1) with
$\mathbf{x},\mathbf{y}$
of the system (1.1) with
![]() $1\leqslant \mathbf{x},\mathbf{y}\leqslant X$
, one has the additional equation
$1\leqslant \mathbf{x},\mathbf{y}\leqslant X$
, one has the additional equation
for some integer
![]() $h$
with
$h$
with
![]() $|h|\leqslant sX^{r}$
. We seek to count all such solutions with
$|h|\leqslant sX^{r}$
. We seek to count all such solutions with
![]() $h$
thus constrained. For each integer
$h$
thus constrained. For each integer
![]() $z$
with
$z$
with
![]() $1\leqslant z\leqslant X$
, we find that whenever
$1\leqslant z\leqslant X$
, we find that whenever
![]() $\mathbf{x},\mathbf{y},h$
satisfy (1.1) and (1.3), then one has
$\mathbf{x},\mathbf{y},h$
satisfy (1.1) and (1.3), then one has
where
![]() $\unicode[STIX]{x1D714}_{j}$
is
$\unicode[STIX]{x1D714}_{j}$
is
![]() $0$
for
$0$
for
![]() $1\leqslant j<r$
and
$1\leqslant j<r$
and
![]() $\binom{j}{r}$
for
$\binom{j}{r}$
for
![]() $r\leqslant j\leqslant k$
, and in which we write
$r\leqslant j\leqslant k$
, and in which we write
![]() $u_{i}=x_{i}+z$
and
$u_{i}=x_{i}+z$
and
![]() $v_{i}=y_{i}+z\;(1\leqslant i\leqslant s)$
. If we are able to obtain significant cancellation in the number of solutions of the system (1.4), now with
$v_{i}=y_{i}+z\;(1\leqslant i\leqslant s)$
. If we are able to obtain significant cancellation in the number of solutions of the system (1.4), now with
![]() $\mathbf{u},\mathbf{v}$
constrained only by the conditions
$\mathbf{u},\mathbf{v}$
constrained only by the conditions
![]() $1\leqslant u_{i},v_{i}\leqslant 2X\;(1\leqslant i\leqslant s)$
, then the overcounting by
$1\leqslant u_{i},v_{i}\leqslant 2X\;(1\leqslant i\leqslant s)$
, then the overcounting by
![]() $z$
may be reversed to show that there is significant cancellation in the system (1.1) underpinning the mean value
$z$
may be reversed to show that there is significant cancellation in the system (1.1) underpinning the mean value
![]() $I_{s,k,r}(X)$
. This brings us to consider the number of solutions of the system
$I_{s,k,r}(X)$
. This brings us to consider the number of solutions of the system
with
![]() $|h_{i}|\leqslant sX^{r}$
and
$|h_{i}|\leqslant sX^{r}$
and
![]() $1\leqslant z_{i}\leqslant X\;(1\leqslant i\leqslant 2t)$
. This auxiliary mean value may be analysed through the use of multiplicative polynomial identities engineered using ideas related to those employed in [Reference Wooley, Pollington and Moran7].
$1\leqslant z_{i}\leqslant X\;(1\leqslant i\leqslant 2t)$
. This auxiliary mean value may be analysed through the use of multiplicative polynomial identities engineered using ideas related to those employed in [Reference Wooley, Pollington and Moran7].
The reader may be interested to learn the consequences of this strategy when
![]() $r$
is permitted to exceed
$r$
is permitted to exceed
![]() $1$
. The conclusion of Theorem 1.1 is in fact a special case of a more general result which, for
$1$
. The conclusion of Theorem 1.1 is in fact a special case of a more general result which, for
![]() $r\geqslant 2$
, unfortunately fails to deliver diagonal behaviour.
$r\geqslant 2$
, unfortunately fails to deliver diagonal behaviour.
Theorem 1.2. Let
![]() $r,s,k\in \mathbb{N}$
satisfy
$r,s,k\in \mathbb{N}$
satisfy
![]() $k>r\geqslant 1$
and
$k>r\geqslant 1$
and
where
![]() $\unicode[STIX]{x1D705}$
is an integer satisfying
$\unicode[STIX]{x1D705}$
is an integer satisfying
![]() $1\leqslant \unicode[STIX]{x1D705}\leqslant (k-r+2)/2$
. Then for each
$1\leqslant \unicode[STIX]{x1D705}\leqslant (k-r+2)/2$
. Then for each
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
When
![]() $r>1$
, although we do not achieve diagonal behaviour, we do improve on the estimate
$r>1$
, although we do not achieve diagonal behaviour, we do improve on the estimate
![]() $I_{s,k,r}(X)\ll X^{s+r+\unicode[STIX]{x1D700}}$
that follows for
$I_{s,k,r}(X)\ll X^{s+r+\unicode[STIX]{x1D700}}$
that follows for
![]() $1\leqslant s\leqslant k(k+1)/2$
from the main conjecture in Vinogradov’s mean value theorem via the triangle inequality. When
$1\leqslant s\leqslant k(k+1)/2$
from the main conjecture in Vinogradov’s mean value theorem via the triangle inequality. When
![]() $r>2$
, the bound for
$r>2$
, the bound for
![]() $I_{s,k,r}(X)$
obtained in the conclusion of Theorem 1.2 remains weaker than what could be obtained by interpolating between the aforementioned bounds
$I_{s,k,r}(X)$
obtained in the conclusion of Theorem 1.2 remains weaker than what could be obtained by interpolating between the aforementioned bounds
![]() $I_{s,k,r}(X)\ll X^{s+\unicode[STIX]{x1D700}}\;(1\leqslant s\leqslant k(k-1)/2)$
and
$I_{s,k,r}(X)\ll X^{s+\unicode[STIX]{x1D700}}\;(1\leqslant s\leqslant k(k-1)/2)$
and
![]() $I_{s,k,r}(X)\ll X^{s+r+\unicode[STIX]{x1D700}}\;(1\leqslant s\leqslant k(k+1)/2)$
. The former bound is, however, yet to enter the published literature.
$I_{s,k,r}(X)\ll X^{s+r+\unicode[STIX]{x1D700}}\;(1\leqslant s\leqslant k(k+1)/2)$
. The former bound is, however, yet to enter the published literature.
In §2 we speculate concerning what bounds might hold for a class of mean values associated with the system (1.5). In particular, should a suitable analogue of the main conjecture hold for this auxiliary mean value, then the conclusion of Theorem 1.2 would be valid with a value of
![]() $\unicode[STIX]{x1D705}$
now permitted to be as large as
$\unicode[STIX]{x1D705}$
now permitted to be as large as
We refer the reader to Conjecture 2.2 below for precise details, and we note in particular the constraint (2.4). When
![]() $r=1$
and
$r=1$
and
![]() $k\equiv 0$
or
$k\equiv 0$
or
![]() $3$
modulo
$3$
modulo
![]() $4$
, this would conditionally establish the estimate
$4$
, this would conditionally establish the estimate
![]() $I_{s,k,1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
in the range
$I_{s,k,1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
in the range
![]() $1\leqslant s\leqslant (k^{2}+k-2)/2$
, and hence the main conjecture (1.2) in full for these cases. When
$1\leqslant s\leqslant (k^{2}+k-2)/2$
, and hence the main conjecture (1.2) in full for these cases. When
![]() $r>1$
, this conditional result establishes a bound slightly stronger than
$r>1$
, this conditional result establishes a bound slightly stronger than
![]() $I_{s,k,r}(X)\ll X^{s+r-1}$
when
$I_{s,k,r}(X)\ll X^{s+r-1}$
when
![]() $1\leqslant s\leqslant (k^{2}+k-4)/2$
, which seems quite respectable.
$1\leqslant s\leqslant (k^{2}+k-4)/2$
, which seems quite respectable.
We begin in §2 by announcing an auxiliary mean value estimate generalizing that associated with the system (1.5). This we establish in §§3–6, obtaining a polynomial identity in §3 of appropriate multiplicative type, establishing a lemma to count integral points on auxiliary equations in §4, and classifying solutions according to the vanishing of certain sets of coefficients in §5. In §6 we combine these ideas with a divisor estimate to complete the proof of this auxiliary estimate. Finally, in §7, we provide the details of the argument sketched above which establishes Theorems 1.1 and 1.2.
Throughout, the letters
![]() $r$
,
$r$
,
![]() $s$
and
$s$
and
![]() $k$
will denote positive integers with
$k$
will denote positive integers with
![]() $r<k$
, and
$r<k$
, and
![]() $\unicode[STIX]{x1D700}$
will denote a sufficiently small positive number. We take
$\unicode[STIX]{x1D700}$
will denote a sufficiently small positive number. We take
![]() $X$
to be a large positive number depending at most on
$X$
to be a large positive number depending at most on
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D700}$
. The implicit constants in the notations of Landau and Vinogradov will depend at most on
$\unicode[STIX]{x1D700}$
. The implicit constants in the notations of Landau and Vinogradov will depend at most on
![]() $s$
,
$s$
,
![]() $k$
,
$k$
,
![]() $\unicode[STIX]{x1D700}$
, and the coefficients of fixed polynomials that we introduce. We adopt the following convention concerning the number
$\unicode[STIX]{x1D700}$
, and the coefficients of fixed polynomials that we introduce. We adopt the following convention concerning the number
![]() $\unicode[STIX]{x1D700}$
. Whenever
$\unicode[STIX]{x1D700}$
. Whenever
![]() $\unicode[STIX]{x1D700}$
appears in a statement, we assert that the statement holds for each
$\unicode[STIX]{x1D700}$
appears in a statement, we assert that the statement holds for each
![]() $\unicode[STIX]{x1D700}>0$
. Finally, we employ the non-standard convention that whenever
$\unicode[STIX]{x1D700}>0$
. Finally, we employ the non-standard convention that whenever
![]() $G: [0,1)^{k}\rightarrow \mathbb{C}$
is integrable, then
$G: [0,1)^{k}\rightarrow \mathbb{C}$
is integrable, then
Here and elsewhere, we use vector notation liberally in a manner that is easily discerned from the context.
2 An auxiliary mean value
Our focus in this section and those following lies on the system of equations (1.5), since this is intimately connected with the Vinogradov system missing the slice of degree
![]() $r$
. Since little additional effort is required to proceed in wider generality, we establish a conclusion in which the monomials
$r$
. Since little additional effort is required to proceed in wider generality, we establish a conclusion in which the monomials
![]() $z^{j-r}\;(r\leqslant j\leqslant k)$
in (1.5) are replaced by independent polynomials
$z^{j-r}\;(r\leqslant j\leqslant k)$
in (1.5) are replaced by independent polynomials
![]() $f_{j}(z)$
. We begin in this section by introducing the notation required to state our main auxiliary result.
$f_{j}(z)$
. We begin in this section by introducing the notation required to state our main auxiliary result.
Let
![]() $t$
be a natural number. When
$t$
be a natural number. When
![]() $1\leqslant j\leqslant t$
, consider a non-zero polynomial
$1\leqslant j\leqslant t$
, consider a non-zero polynomial
![]() $f_{j}\in \mathbb{Z}[x]$
of degree
$f_{j}\in \mathbb{Z}[x]$
of degree
![]() $k_{j}$
. We say that
$k_{j}$
. We say that
![]() $\mathbf{f}=(f_{1},\ldots ,f_{t})$
is well-conditioned when the degrees of the polynomials
$\mathbf{f}=(f_{1},\ldots ,f_{t})$
is well-conditioned when the degrees of the polynomials
![]() $f_{j}$
satisfy the condition
$f_{j}$
satisfy the condition
and there is no positive integer
![]() $z$
for which
$z$
for which
![]() $f_{1}(z)=\cdots =f_{t}(z)=0$
.
$f_{1}(z)=\cdots =f_{t}(z)=0$
.
Let
![]() $X$
be a positive number sufficiently large in terms of
$X$
be a positive number sufficiently large in terms of
![]() $t$
,
$t$
,
![]() $\mathbf{k}$
and the coefficients of
$\mathbf{k}$
and the coefficients of
![]() $f$
. We define the exponential sum
$f$
. We define the exponential sum
![]() $\mathfrak{g}(\boldsymbol{\unicode[STIX]{x1D6FC}};X)$
by putting
$\mathfrak{g}(\boldsymbol{\unicode[STIX]{x1D6FC}};X)$
by putting
Finally, we define the mean value
By orthogonality, the mean value
![]() $A_{s,r}(X;\mathbf{f}\,)$
counts the number of integral solutions of the system of equations
$A_{s,r}(X;\mathbf{f}\,)$
counts the number of integral solutions of the system of equations
with
![]() $|h_{i}|\leqslant X^{r}$
and
$|h_{i}|\leqslant X^{r}$
and
![]() $1\leqslant z_{i}\leqslant X\;(1\leqslant i\leqslant 2s)$
. The system (2.3) plainly generalizes (1.5). Our immediate goal is to establish the mean value estimate recorded in the following theorem.
$1\leqslant z_{i}\leqslant X\;(1\leqslant i\leqslant 2s)$
. The system (2.3) plainly generalizes (1.5). Our immediate goal is to establish the mean value estimate recorded in the following theorem.
Theorem 2.1. Let
![]() $r$
,
$r$
,
![]() $s$
and
$s$
and
![]() $t$
be natural numbers with
$t$
be natural numbers with
![]() $t\geqslant 2s-1$
. Then whenever
$t\geqslant 2s-1$
. Then whenever
![]() $\mathbf{f}$
is a well-conditioned
$\mathbf{f}$
is a well-conditioned
![]() $t$
-tuple of polynomials having integral coefficients, one has
$t$
-tuple of polynomials having integral coefficients, one has
![]() $A_{s,r}(X;\mathbf{f}\,)\ll X^{r(2s-1)+1+\unicode[STIX]{x1D700}}$
.
$A_{s,r}(X;\mathbf{f}\,)\ll X^{r(2s-1)+1+\unicode[STIX]{x1D700}}$
.
Note that when
![]() $r=1$
, the conclusion of this theorem is tantamount to exhibiting square-root cancellation in the mean value (2.2), so is essentially best possible. Indeed, even in situations wherein
$r=1$
, the conclusion of this theorem is tantamount to exhibiting square-root cancellation in the mean value (2.2), so is essentially best possible. Indeed, even in situations wherein
![]() $r>1$
, the solutions of (2.3) in which
$r>1$
, the solutions of (2.3) in which
![]() $z_{1}=z_{2}=\cdots =z_{2s}$
make a contribution to
$z_{1}=z_{2}=\cdots =z_{2s}$
make a contribution to
![]() $A_{s,r}(X;\mathbf{f}\,)$
of order
$A_{s,r}(X;\mathbf{f}\,)$
of order
![]() $X\cdot (X^{r})^{2s-1}$
, and so the conclusion of Theorem 2.1 is again essentially best possible. Henceforth, we restrict our attention to the situation described by the hypotheses of Theorem 2.1. Thus, we may suppose that
$X\cdot (X^{r})^{2s-1}$
, and so the conclusion of Theorem 2.1 is again essentially best possible. Henceforth, we restrict our attention to the situation described by the hypotheses of Theorem 2.1. Thus, we may suppose that
![]() $t\geqslant 2s-1$
, and that
$t\geqslant 2s-1$
, and that
![]() $\mathbf{f}$
is a well-conditioned
$\mathbf{f}$
is a well-conditioned
![]() $t$
-tuple of polynomials
$t$
-tuple of polynomials
![]() $f_{j}\in \mathbb{Z}[x]$
with
$f_{j}\in \mathbb{Z}[x]$
with
![]() $\deg (f_{j})=k_{j}\geqslant 0$
.
$\deg (f_{j})=k_{j}\geqslant 0$
.
It seems not unreasonable to speculate that the estimate claimed in the statement of Theorem 2.1 should remain valid when
![]() $s$
is significantly larger than
$s$
is significantly larger than
![]() $(t+1)/2$
. The total number of choices for the
$(t+1)/2$
. The total number of choices for the
![]() $2s$
pairs of variables
$2s$
pairs of variables
![]() $h_{i},z_{i}$
occurring in the system (2.3) is of order
$h_{i},z_{i}$
occurring in the system (2.3) is of order
![]() $(X^{r+1})^{2s}$
. Meanwhile, the
$(X^{r+1})^{2s}$
. Meanwhile, the
![]() $t$
equations comprising (2.3) involve monomials having typical size of asymptotic order
$t$
equations comprising (2.3) involve monomials having typical size of asymptotic order
![]() $X^{r+k_{j}}\;(1\leqslant j\leqslant t)$
. Thus, for large
$X^{r+k_{j}}\;(1\leqslant j\leqslant t)$
. Thus, for large
![]() $s$
, one should expect that
$s$
, one should expect that
Keeping in mind the diagonal solutions discussed above, one is led to the following conjecture.
Conjecture 2.2. Let
![]() $r$
,
$r$
,
![]() $s$
and
$s$
and
![]() $t$
be natural numbers, and suppose that
$t$
be natural numbers, and suppose that
![]() $\mathbf{f}$
is a well-conditioned
$\mathbf{f}$
is a well-conditioned
![]() $t$
-tuple of polynomials having integral coefficients, with
$t$
-tuple of polynomials having integral coefficients, with
![]() $\deg (f_{j})=k_{j}\;(1\leqslant j\leqslant t)$
. Then one has
$\deg (f_{j})=k_{j}\;(1\leqslant j\leqslant t)$
. Then one has
In the special case in which
![]() $t=k-r+1$
and
$t=k-r+1$
and
![]() $k_{j}=j-1\;(1\leqslant j\leqslant t)$
relevant to the system (1.5), this conjectural bound reads
$k_{j}=j-1\;(1\leqslant j\leqslant t)$
relevant to the system (1.5), this conjectural bound reads
In such circumstances, one finds that
provided that
![]() $s$
is an integer satisfying
$s$
is an integer satisfying
We finish this section by remarking that the estimate
![]() $A_{s,r}(X;\mathbf{f}\,)\ll X^{2rs}$
is fairly easily established when
$A_{s,r}(X;\mathbf{f}\,)\ll X^{2rs}$
is fairly easily established when
![]() $t\geqslant 2s$
, a stronger condition than that imposed in Theorem 2.1, as we now sketch. We may suppose that
$t\geqslant 2s$
, a stronger condition than that imposed in Theorem 2.1, as we now sketch. We may suppose that
![]() $t=2s$
without loss, and in such circumstances the equations (2.3) may be interpreted as a system of
$t=2s$
without loss, and in such circumstances the equations (2.3) may be interpreted as a system of
![]() $2s$
linear equations in
$2s$
linear equations in
![]() $2s$
variables
$2s$
variables
![]() $h_{i}$
. There are
$h_{i}$
. There are
![]() $O(X^{2s})$
choices for the variables
$O(X^{2s})$
choices for the variables
![]() $z_{i}$
, contributing
$z_{i}$
, contributing
![]() $O(X^{2s})$
to
$O(X^{2s})$
to
![]() $A_{s,r}(X;\mathbf{f}\,)$
from those solutions with
$A_{s,r}(X;\mathbf{f}\,)$
from those solutions with
![]() $\mathbf{h}=\mathbf{0}$
. Meanwhile, if
$\mathbf{h}=\mathbf{0}$
. Meanwhile, if
![]() $\mathbf{h}\neq \mathbf{0}$
one must have
$\mathbf{h}\neq \mathbf{0}$
one must have
By applying the theory of Schur functions (see Macdonald [Reference Macdonald5, Ch. I]) as in the proof of [Reference Parsell and Wooley6, Lemma 1], one finds that
where the polynomial
![]() $\unicode[STIX]{x1D6E9}(\mathbf{z};\mathbf{f}\,)$
is asymptotically definite, meaning that whenever
$\unicode[STIX]{x1D6E9}(\mathbf{z};\mathbf{f}\,)$
is asymptotically definite, meaning that whenever
![]() $z_{i}$
is sufficiently large for
$z_{i}$
is sufficiently large for
![]() $1\leqslant i\leqslant 2s$
, then
$1\leqslant i\leqslant 2s$
, then
![]() $|\unicode[STIX]{x1D6E9}(\mathbf{z};\mathbf{f}\,)|\geqslant 1$
.
$|\unicode[STIX]{x1D6E9}(\mathbf{z};\mathbf{f}\,)|\geqslant 1$
.
The contribution to
![]() $A_{s,r}(X;\mathbf{f}\,)$
arising from the solutions of (2.3) with
$A_{s,r}(X;\mathbf{f}\,)$
arising from the solutions of (2.3) with
![]() $z_{i}=O(1)$
, for some index
$z_{i}=O(1)$
, for some index
![]() $i$
, is
$i$
, is
![]() $O((X^{r})^{2s})$
. For if
$O((X^{r})^{2s})$
. For if
![]() $z_{i}=O(1)$
, then we may fix
$z_{i}=O(1)$
, then we may fix
![]() $h_{i}$
, and interpret the system as a mean value of exponential sums, applying the triangle inequality. An application of Hölder’s inequality reveals that if such solutions dominate, then
$h_{i}$
, and interpret the system as a mean value of exponential sums, applying the triangle inequality. An application of Hölder’s inequality reveals that if such solutions dominate, then
and the desired conclusion follows. Meanwhile, if
![]() $z_{i}$
is sufficiently large for each index
$z_{i}$
is sufficiently large for each index
![]() $i$
, then
$i$
, then
![]() $|\unicode[STIX]{x1D6E9}(\mathbf{z};\mathbf{f}\,)|$
is strictly positive and hence (2.5) can hold only when
$|\unicode[STIX]{x1D6E9}(\mathbf{z};\mathbf{f}\,)|$
is strictly positive and hence (2.5) can hold only when
![]() $z_{i}=z_{j}$
for some indices
$z_{i}=z_{j}$
for some indices
![]() $i$
and
$i$
and
![]() $j$
with
$j$
with
![]() $1\leqslant i<j\leqslant 2s$
. By symmetry we may suppose that
$1\leqslant i<j\leqslant 2s$
. By symmetry we may suppose that
![]() $i=2s-1$
and
$i=2s-1$
and
![]() $j=2s$
, and then we obtain from (2.3) the new system of equations
$j=2s$
, and then we obtain from (2.3) the new system of equations
with
![]() $h_{i}^{\prime }=h_{i}\;(1\leqslant i\leqslant 2s-2)$
and
$h_{i}^{\prime }=h_{i}\;(1\leqslant i\leqslant 2s-2)$
and
![]() $h_{2s-1}^{\prime }=h_{2s-1}+h_{2s}$
. This new system is of similar shape to (2.3), and we may apply an obvious inductive argument to bound the number of its solutions. Here, we keep in mind that given
$h_{2s-1}^{\prime }=h_{2s-1}+h_{2s}$
. This new system is of similar shape to (2.3), and we may apply an obvious inductive argument to bound the number of its solutions. Here, we keep in mind that given
![]() $h_{2s-1}^{\prime }$
, there are
$h_{2s-1}^{\prime }$
, there are
![]() $O(X^{r})$
possible choices for
$O(X^{r})$
possible choices for
![]() $h_{2s-1}$
and
$h_{2s-1}$
and
![]() $h_{2s}$
. Thus we conclude that if this second class of solutions dominates, then one has
$h_{2s}$
. Thus we conclude that if this second class of solutions dominates, then one has
This completes our sketch of the proof that when
![]() $t=2s$
, the total number of solutions counted by
$t=2s$
, the total number of solutions counted by
![]() $A_{s,r}(X;\mathbf{f}\,)$
is
$A_{s,r}(X;\mathbf{f}\,)$
is
![]() $O(X^{2rs})$
. The reader will likely have no difficulty in refining this argument to deliver the conclusion of Theorem 2.1 when
$O(X^{2rs})$
. The reader will likely have no difficulty in refining this argument to deliver the conclusion of Theorem 2.1 when
![]() $t=2s$
.
$t=2s$
.
3 A polynomial identity
The structure of the polynomials
![]() $hf_{j}(z)$
underlying the mean value
$hf_{j}(z)$
underlying the mean value
![]() $A_{s,r}(X;\mathbf{f}\,)$
permits polynomial identities to be constructed of utility in constraining solutions of the underlying system of equations (2.3). In this section we construct such identities.
$A_{s,r}(X;\mathbf{f}\,)$
permits polynomial identities to be constructed of utility in constraining solutions of the underlying system of equations (2.3). In this section we construct such identities.
For the sake of concision, when
![]() $n$
is a natural number and
$n$
is a natural number and
![]() $1\leqslant j\leqslant t$
, we define the polynomial
$1\leqslant j\leqslant t$
, we define the polynomial
![]() $\unicode[STIX]{x1D70E}_{j,n}=\unicode[STIX]{x1D70E}_{j,n}(\mathbf{z};\mathbf{h})$
by putting
$\unicode[STIX]{x1D70E}_{j,n}=\unicode[STIX]{x1D70E}_{j,n}(\mathbf{z};\mathbf{h})$
by putting
Lemma 3.1. Suppose that
![]() $n\geqslant 1$
and that
$n\geqslant 1$
and that
![]() $\mathbf{f}=(f_{1},\ldots ,f_{2n+1})$
is a well-conditioned
$\mathbf{f}=(f_{1},\ldots ,f_{2n+1})$
is a well-conditioned
![]() $(2n+1)$
-tuple of polynomials having integral coefficients. Then there exists a polynomial
$(2n+1)$
-tuple of polynomials having integral coefficients. Then there exists a polynomial
![]() $\unicode[STIX]{x1D6F9}_{n}(\mathbf{w})\in \mathbb{Z}[w_{1},\ldots ,w_{2n+1}]$
whose total degree and coefficients depend at most on
$\unicode[STIX]{x1D6F9}_{n}(\mathbf{w})\in \mathbb{Z}[w_{1},\ldots ,w_{2n+1}]$
whose total degree and coefficients depend at most on
![]() $n$
,
$n$
,
![]() $\mathbf{k}$
and the coefficients of
$\mathbf{k}$
and the coefficients of
![]() $\mathbf{f}$
, having the property that
$\mathbf{f}$
, having the property that
identically in
![]() $\mathbf{z}$
and
$\mathbf{z}$
and
![]() $\mathbf{h}$
, and yet
$\mathbf{h}$
, and yet
Proof. We apply an argument similar to that of [Reference Wooley, Pollington and Moran7, Lemma 1] based on a consideration of transcendence degrees. Let
![]() $K=\mathbb{Q}(\unicode[STIX]{x1D70E}_{1,n},\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n})$
. Then
$K=\mathbb{Q}(\unicode[STIX]{x1D70E}_{1,n},\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n})$
. Then
![]() $K\subseteq \mathbb{Q}(z_{1},\ldots ,z_{n},h_{1},\ldots ,h_{n})$
, so that
$K\subseteq \mathbb{Q}(z_{1},\ldots ,z_{n},h_{1},\ldots ,h_{n})$
, so that
![]() $K$
has transcendence degree at most
$K$
has transcendence degree at most
![]() $2n$
over
$2n$
over
![]() $\mathbb{Q}$
. It follows that the
$\mathbb{Q}$
. It follows that the
![]() $2n+1$
polynomials
$2n+1$
polynomials
![]() $\unicode[STIX]{x1D70E}_{1,n}(\mathbf{z};\mathbf{h}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n}(\mathbf{z};\mathbf{h})$
cannot be algebraically independent over
$\unicode[STIX]{x1D70E}_{1,n}(\mathbf{z};\mathbf{h}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n}(\mathbf{z};\mathbf{h})$
cannot be algebraically independent over
![]() $\mathbb{Q}$
. Consequently, there exists a non-zero polynomial
$\mathbb{Q}$
. Consequently, there exists a non-zero polynomial
![]() $\unicode[STIX]{x1D6F9}_{n}\in \mathbb{Z}[w_{1},\ldots ,w_{2n+1}]$
satisfying the property (3.1).
$\unicode[STIX]{x1D6F9}_{n}\in \mathbb{Z}[w_{1},\ldots ,w_{2n+1}]$
satisfying the property (3.1).
It remains now only to confirm that a choice may be made for this non-trivial polynomial
![]() $\unicode[STIX]{x1D6F9}_{n}$
in such a manner that property (3.2) also holds. In order to establish this claim, we begin by considering any non-zero polynomial
$\unicode[STIX]{x1D6F9}_{n}$
in such a manner that property (3.2) also holds. In order to establish this claim, we begin by considering any non-zero polynomial
![]() $\unicode[STIX]{x1D6F9}_{n}$
of smallest total degree satisfying (3.1). Suppose, if possible, that
$\unicode[STIX]{x1D6F9}_{n}$
of smallest total degree satisfying (3.1). Suppose, if possible, that
![]() $\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1},\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1})$
is also identically zero. Then the polynomials
$\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1},\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1})$
is also identically zero. Then the polynomials
and
must also be identically zero for
![]() $1\leqslant i\leqslant n+1$
. Write
$1\leqslant i\leqslant n+1$
. Write
in which we evaluate the right-hand side at
![]() $w_{i}=\unicode[STIX]{x1D70E}_{i,n+1}(\mathbf{z};\mathbf{h})\;(1\leqslant i\leqslant 2n+1)$
. Then it follows from an application of the chain rule that the vanishing of the polynomials (3.3) and (3.4) implies the relations
$w_{i}=\unicode[STIX]{x1D70E}_{i,n+1}(\mathbf{z};\mathbf{h})\;(1\leqslant i\leqslant 2n+1)$
. Then it follows from an application of the chain rule that the vanishing of the polynomials (3.3) and (3.4) implies the relations
and
Notice here that we have deliberately omitted the index
![]() $i=n+1$
from the relations (3.5), since this is superfluous to our needs.
$i=n+1$
from the relations (3.5), since this is superfluous to our needs.
In order to encode the coefficient matrix associated with the system of linear equations in
![]() $\mathbf{u}$
described by the relations (3.5) and (3.6), we introduce a block matrix as follows. We define the
$\mathbf{u}$
described by the relations (3.5) and (3.6), we introduce a block matrix as follows. We define the
![]() $n\times (2n+1)$
matrix
$n\times (2n+1)$
matrix
and the
![]() $(n+1)\times (2n+1)$
matrix
$(n+1)\times (2n+1)$
matrix
and then define the
![]() $(2n+1)\times (2n+1)$
matrix
$(2n+1)\times (2n+1)$
matrix
![]() $D_{n}$
via the block decomposition
$D_{n}$
via the block decomposition
We claim that
![]() $\det (D_{n})$
is not identically zero as a polynomial. The confirmation of this fact we defer to the end of this proof.
$\det (D_{n})$
is not identically zero as a polynomial. The confirmation of this fact we defer to the end of this proof.
With the assumption
![]() $\det (D_{n})\neq 0$
in hand, one sees that the system of equations (3.5) and (3.6) has only the trivial solution
$\det (D_{n})\neq 0$
in hand, one sees that the system of equations (3.5) and (3.6) has only the trivial solution
![]() $\mathbf{u}=\mathbf{0}$
over
$\mathbf{u}=\mathbf{0}$
over
![]() $K$
. However, since
$K$
. However, since
![]() $\unicode[STIX]{x1D6F9}_{n}(\mathbf{w})$
is a non-constant polynomial, at least one of the derivatives
$\unicode[STIX]{x1D6F9}_{n}(\mathbf{w})$
is a non-constant polynomial, at least one of the derivatives
must be non-zero. Suppose that the partial derivative with respect to
![]() $w_{J}$
is non-zero. Then there exists a non-constant polynomial
$w_{J}$
is non-zero. Then there exists a non-constant polynomial
having the property that, since
![]() $u_{J}=0$
, one has
$u_{J}=0$
, one has
But the total degree of
![]() $\unicode[STIX]{x1D6F9}_{n}^{\ast }$
is strictly smaller than that of
$\unicode[STIX]{x1D6F9}_{n}^{\ast }$
is strictly smaller than that of
![]() $\unicode[STIX]{x1D6F9}_{n}$
, contradicting our hypothesis that
$\unicode[STIX]{x1D6F9}_{n}$
, contradicting our hypothesis that
![]() $\unicode[STIX]{x1D6F9}_{n}$
has minimal total degree. We are therefore forced to conclude that the relation (3.2) does indeed hold.
$\unicode[STIX]{x1D6F9}_{n}$
has minimal total degree. We are therefore forced to conclude that the relation (3.2) does indeed hold.
We now turn to the problem of justifying our assumption that
![]() $\det (D_{n})\neq 0$
. We prove this assertion for any well-conditioned
$\det (D_{n})\neq 0$
. We prove this assertion for any well-conditioned
![]() $(2n+1)$
-tuple of polynomials
$(2n+1)$
-tuple of polynomials
![]() $\mathbf{f}$
by induction on
$\mathbf{f}$
by induction on
![]() $n$
. Observe first that when
$n$
. Observe first that when
![]() $n=0$
, one has
$n=0$
, one has
![]() $\det (D_{0})=f_{1}(z_{1})$
. Since
$\det (D_{0})=f_{1}(z_{1})$
. Since
![]() $f_{1}(z)$
is not identically zero, it follows that
$f_{1}(z)$
is not identically zero, it follows that
![]() $\det (D_{0})\neq 0$
, confirming the base case of our inductive hypothesis. We suppose next that
$\det (D_{0})\neq 0$
, confirming the base case of our inductive hypothesis. We suppose next that
![]() $n\geqslant 1$
and that
$n\geqslant 1$
and that
![]() $\det (D_{n-1})\neq 0$
for all well-conditioned
$\det (D_{n-1})\neq 0$
for all well-conditioned
![]() $(2n-1)$
-tuples of polynomials
$(2n-1)$
-tuples of polynomials
![]() $\mathbf{f}$
, and we seek to show that
$\mathbf{f}$
, and we seek to show that
![]() $\det (D_{n})\neq 0$
.
$\det (D_{n})\neq 0$
.
Denote by
![]() ${\mathcal{I}}$
the set of all
${\mathcal{I}}$
the set of all
![]() $2$
-element subsets
$2$
-element subsets
![]() $\mathfrak{a}=\{a_{1},a_{2}\}$
contained in
$\mathfrak{a}=\{a_{1},a_{2}\}$
contained in
![]() ${\mathcal{N}}=\{1,2,\ldots ,2n+1\}$
. When
${\mathcal{N}}=\{1,2,\ldots ,2n+1\}$
. When
![]() $\mathfrak{a}=\{a_{1},a_{2}\}\in {\mathcal{I}}$
, we define the matrices
$\mathfrak{a}=\{a_{1},a_{2}\}\in {\mathcal{I}}$
, we define the matrices
Equipped with this notation, we define the minors
In this way, we discern that for appropriate choices of
![]() $\unicode[STIX]{x1D70E}(\mathfrak{a})\in \{1,-1\}$
, the precise nature of which need not detain us, one has
$\unicode[STIX]{x1D70E}(\mathfrak{a})\in \{1,-1\}$
, the precise nature of which need not detain us, one has
By relabelling indices and then applying the inductive hypothesis for the
![]() $(2n-1)$
-tuple
$(2n-1)$
-tuple
![]() $(f_{3},\ldots ,f_{2n+1})$
, it is apparent that
$(f_{3},\ldots ,f_{2n+1})$
, it is apparent that
![]() $V(\{1,2\})$
is not identically zero. In view of (2.1), moreover, if the leading coefficients of
$V(\{1,2\})$
is not identically zero. In view of (2.1), moreover, if the leading coefficients of
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
are
$f_{2}$
are
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
, respectively, then the leading monomial in
$c_{2}$
, respectively, then the leading monomial in
![]() $U(\{1,2\})$
is
$U(\{1,2\})$
is
It follows that
![]() $U(\{1,2\})$
is also not identically zero. Also, since no other minor of the shape
$U(\{1,2\})$
is also not identically zero. Also, since no other minor of the shape
![]() $U(\mathfrak{a})$
, with
$U(\mathfrak{a})$
, with
![]() $\mathfrak{a}\in {\mathcal{I}}$
and
$\mathfrak{a}\in {\mathcal{I}}$
and
![]() $\mathfrak{a}\neq \{1,2\}$
, has degree
$\mathfrak{a}\neq \{1,2\}$
, has degree
![]() $k_{1}+k_{2}-1$
or greater with respect to
$k_{1}+k_{2}-1$
or greater with respect to
![]() $z_{1}$
, we deduce that
$z_{1}$
, we deduce that
![]() $\det (D_{n})$
is not identically zero. This confirms the inductive hypothesis for the index
$\det (D_{n})$
is not identically zero. This confirms the inductive hypothesis for the index
![]() $n$
and completes the proof of our claim for all
$n$
and completes the proof of our claim for all
![]() $n$
.◻
$n$
.◻
Henceforth, when
![]() $n\geqslant 1$
, we consider a fixed choice for the polynomials
$n\geqslant 1$
, we consider a fixed choice for the polynomials
![]() $\unicode[STIX]{x1D6F9}_{n}(\mathbf{w})\in \mathbb{Z}[w_{1},\ldots ,w_{2n+1}]$
, of minimal total degree, satisfying the conditions (3.1) and (3.2). It is useful to extend this definition by taking
$\unicode[STIX]{x1D6F9}_{n}(\mathbf{w})\in \mathbb{Z}[w_{1},\ldots ,w_{2n+1}]$
, of minimal total degree, satisfying the conditions (3.1) and (3.2). It is useful to extend this definition by taking
![]() $\unicode[STIX]{x1D6F9}_{0}(w)=w$
. We may now establish our fundamental polynomial identity.
$\unicode[STIX]{x1D6F9}_{0}(w)=w$
. We may now establish our fundamental polynomial identity.
Lemma 3.2. Suppose that
![]() $n\geqslant 0$
and the
$n\geqslant 0$
and the
![]() $(2n+1)$
-tuple
$(2n+1)$
-tuple
![]() $\mathbf{f}=(f_{1},\ldots ,f_{2n+1})$
of polynomials in
$\mathbf{f}=(f_{1},\ldots ,f_{2n+1})$
of polynomials in
![]() $\mathbb{Z}[x]$
is well-conditioned. Then there exists a non-zero polynomial
$\mathbb{Z}[x]$
is well-conditioned. Then there exists a non-zero polynomial
![]() $\unicode[STIX]{x1D6F7}_{n}(\mathbf{z};\mathbf{h})\in \mathbb{Z}[\mathbf{z},\mathbf{h}]$
with the property that
$\unicode[STIX]{x1D6F7}_{n}(\mathbf{z};\mathbf{h})\in \mathbb{Z}[\mathbf{z},\mathbf{h}]$
with the property that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1}(\mathbf{z};\mathbf{h}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1}(\mathbf{z};\mathbf{h}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}_{n}(\mathbf{z};\mathbf{h})h_{1}\cdots h_{n+1}\mathop{\prod }_{1\leqslant i<j\leqslant n+1}(z_{i}-z_{j}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1}(\mathbf{z};\mathbf{h}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1}(\mathbf{z};\mathbf{h}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}_{n}(\mathbf{z};\mathbf{h})h_{1}\cdots h_{n+1}\mathop{\prod }_{1\leqslant i<j\leqslant n+1}(z_{i}-z_{j}).\end{eqnarray}$$
Proof. In the case
![]() $n=0$
, the product over
$n=0$
, the product over
![]() $i$
and
$i$
and
![]() $j$
on the right-hand side of (3.7) is empty, and by convention we take this empty product to be
$j$
on the right-hand side of (3.7) is empty, and by convention we take this empty product to be
![]() $1$
. In such circumstances, we see that
$1$
. In such circumstances, we see that
![]() $\unicode[STIX]{x1D6F9}_{0}(\unicode[STIX]{x1D70E}_{1,1}(z_{1};h_{1}))=h_{1}f_{1}(z_{1})$
, and the conclusion of the lemma is immediate.
$\unicode[STIX]{x1D6F9}_{0}(\unicode[STIX]{x1D70E}_{1,1}(z_{1};h_{1}))=h_{1}f_{1}(z_{1})$
, and the conclusion of the lemma is immediate.
Suppose next that
![]() $n\geqslant 1$
. Then, when
$n\geqslant 1$
. Then, when
![]() $h_{n+1}=0$
, we have
$h_{n+1}=0$
, we have
and thus we deduce from property (3.1) of Lemma 3.1 that in this situation, one has
It follows that
![]() $h_{n+1}$
divides
$h_{n+1}$
divides
![]() $\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1}(\mathbf{z};\mathbf{h}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1}(\mathbf{z};\mathbf{h}))$
, and by symmetry the same holds for
$\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1}(\mathbf{z};\mathbf{h}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1}(\mathbf{z};\mathbf{h}))$
, and by symmetry the same holds for
![]() $h_{1},\ldots ,h_{n}$
. Meanwhile, when
$h_{1},\ldots ,h_{n}$
. Meanwhile, when
![]() $z_{n}=z_{n+1}$
, we have
$z_{n}=z_{n+1}$
, we have
and again we find from property (3.1) of Lemma 3.1 that in this special situation one has (3.8). We thus conclude that
![]() $z_{n}-z_{n+1}$
divides the polynomial
$z_{n}-z_{n+1}$
divides the polynomial
![]() $\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1}(\mathbf{z};\mathbf{h}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1}(\mathbf{z};\mathbf{h}))$
, and by symmetry the same holds for
$\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1}(\mathbf{z};\mathbf{h}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1}(\mathbf{z};\mathbf{h}))$
, and by symmetry the same holds for
![]() $z_{i}-z_{j}$
whenever
$z_{i}-z_{j}$
whenever
![]() $1\leqslant i<j\leqslant n+1$
.
$1\leqslant i<j\leqslant n+1$
.
In light of these observations, it is apparent that
is divisible by
The quotient of the former polynomial by the latter cannot be zero, since this former polynomial is non-zero, by virtue of property (3.2) of Lemma 3.1. We therefore conclude that a non-zero polynomial
![]() $\unicode[STIX]{x1D6F7}_{n}(\mathbf{z};\mathbf{h})\in \mathbb{Z}[\mathbf{z},\mathbf{h}]$
does indeed exist satisfying (3.7). This completes the proof of the lemma.◻
$\unicode[STIX]{x1D6F7}_{n}(\mathbf{z};\mathbf{h})\in \mathbb{Z}[\mathbf{z},\mathbf{h}]$
does indeed exist satisfying (3.7). This completes the proof of the lemma.◻
It seems quite likely that additional potentially useful structure might be extracted from the polynomial identities provided by Lemma 3.2. For example, the relation
plays a prominent role in the proof of [Reference Wooley8, Lemma 2.1]. Meanwhile, writing
one may verify that
for a suitable bihomogeneous polynomial
![]() $F_{6,3}(\mathbf{z};\mathbf{h})\in \mathbb{Z}[\mathbf{z},\mathbf{h}]$
, of degree
$F_{6,3}(\mathbf{z};\mathbf{h})\in \mathbb{Z}[\mathbf{z},\mathbf{h}]$
, of degree
![]() $6$
with respect to
$6$
with respect to
![]() $\mathbf{z}$
and degree
$\mathbf{z}$
and degree
![]() $3$
with respect to
$3$
with respect to
![]() $\mathbf{h}$
.
$\mathbf{h}$
.
4 Counting integral solutions pairwise
The polynomial identity furnished by Lemma 3.2 is of multiplicative type, and particularly powerful when
![]() $\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1},\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1})$
is non-zero for a fixed integral choice of
$\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1},\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1})$
is non-zero for a fixed integral choice of
![]() $\mathbf{z}$
and
$\mathbf{z}$
and
![]() $\mathbf{h}$
, for then we may exploit elementary estimates for the divisor function. However, it is possible that the latter quantity vanishes. This brings us into the domain of the classification of solutions according to the vanishing or non-vanishing of various intermediate coefficients. We begin with an elementary lemma concerning polynomials in two variables similar to [Reference Wooley, Pollington and Moran7, Lemma 2], the proof of which we include for the sake of completeness.
$\mathbf{h}$
, for then we may exploit elementary estimates for the divisor function. However, it is possible that the latter quantity vanishes. This brings us into the domain of the classification of solutions according to the vanishing or non-vanishing of various intermediate coefficients. We begin with an elementary lemma concerning polynomials in two variables similar to [Reference Wooley, Pollington and Moran7, Lemma 2], the proof of which we include for the sake of completeness.
Lemma 4.1. Let
![]() $\unicode[STIX]{x1D713}\in \mathbb{Z}[z,h]$
be a non-trivial polynomial of total degree
$\unicode[STIX]{x1D713}\in \mathbb{Z}[z,h]$
be a non-trivial polynomial of total degree
![]() $d$
. Then the number of integral solutions of the equation
$d$
. Then the number of integral solutions of the equation
![]() $\unicode[STIX]{x1D713}(z,h)=0$
with
$\unicode[STIX]{x1D713}(z,h)=0$
with
![]() $|z|\leqslant X$
and
$|z|\leqslant X$
and
![]() $|h|\leqslant X^{r}$
is at most
$|h|\leqslant X^{r}$
is at most
![]() $2d(2X^{r}+1)$
.
$2d(2X^{r}+1)$
.
Proof. We may write
![]() $\unicode[STIX]{x1D713}(z,h)=a_{d}(z)h^{d}+\cdots +a_{1}(z)h+a_{0}(z)$
, with
$\unicode[STIX]{x1D713}(z,h)=a_{d}(z)h^{d}+\cdots +a_{1}(z)h+a_{0}(z)$
, with
![]() $a_{i}\in \mathbb{Z}[z]$
of degree at most
$a_{i}\in \mathbb{Z}[z]$
of degree at most
![]() $d$
for
$d$
for
![]() $0\leqslant i\leqslant d$
. The solutions to be counted are of two types. Firstly, one has solutions
$0\leqslant i\leqslant d$
. The solutions to be counted are of two types. Firstly, one has solutions
![]() $(z,h)$
with
$(z,h)$
with
![]() $|z|\leqslant X$
for which
$|z|\leqslant X$
for which
![]() $a_{i}(z)\neq 0$
for some index
$a_{i}(z)\neq 0$
for some index
![]() $i$
, and secondly one has solutions for which
$i$
, and secondly one has solutions for which
![]() $a_{i}(z)=0\;(0\leqslant i\leqslant d)$
. Given any fixed one of the (at most)
$a_{i}(z)=0\;(0\leqslant i\leqslant d)$
. Given any fixed one of the (at most)
![]() $2X+1$
possible choices of
$2X+1$
possible choices of
![]() $z$
in a solution of the first type, one finds that
$z$
in a solution of the first type, one finds that
![]() $h$
satisfies a non-trivial polynomial equation of degree at most
$h$
satisfies a non-trivial polynomial equation of degree at most
![]() $d$
, to which there are at most
$d$
, to which there are at most
![]() $d$
integral solutions. There are consequently at most
$d$
integral solutions. There are consequently at most
![]() $d(2X+1)$
solutions of this first type. On the other hand, whenever
$d(2X+1)$
solutions of this first type. On the other hand, whenever
![]() $(z,h)$
is a solution of the second type, then
$(z,h)$
is a solution of the second type, then
![]() $z$
satisfies some non-trivial polynomial equation
$z$
satisfies some non-trivial polynomial equation
![]() $a_{i}(z)=0$
of degree at most
$a_{i}(z)=0$
of degree at most
![]() $d$
. Since this equation has at most
$d$
. Since this equation has at most
![]() $d$
integral solutions and there are at most
$d$
integral solutions and there are at most
![]() $2X^{r}+1$
possible choices for
$2X^{r}+1$
possible choices for
![]() $h$
, one has at most
$h$
, one has at most
![]() $d(2X^{r}+1)$
solutions of the second type. The conclusion of the lemma now follows.◻
$d(2X^{r}+1)$
solutions of the second type. The conclusion of the lemma now follows.◻
We now announce an initial classification of intermediate coefficients. We define sets
![]() ${\mathcal{T}}_{n,m}\subseteq \mathbb{Z}[z_{1},\ldots ,z_{m},h_{1},\ldots ,h_{m}]$
for
${\mathcal{T}}_{n,m}\subseteq \mathbb{Z}[z_{1},\ldots ,z_{m},h_{1},\ldots ,h_{m}]$
for
![]() $0\leqslant m\leqslant n+1$
inductively as follows. First, let
$0\leqslant m\leqslant n+1$
inductively as follows. First, let
![]() ${\mathcal{T}}_{n,n+1}$
denote the singleton set containing the polynomial
${\mathcal{T}}_{n,n+1}$
denote the singleton set containing the polynomial
Next, suppose that we have already defined the set
![]() ${\mathcal{T}}_{n,m+1}$
, and consider an element
${\mathcal{T}}_{n,m+1}$
, and consider an element
![]() $\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
. We may interpret
$\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
. We may interpret
![]() $\unicode[STIX]{x1D713}$
as a polynomial in
$\unicode[STIX]{x1D713}$
as a polynomial in
![]() $z_{m+1}$
and
$z_{m+1}$
and
![]() $h_{m+1}$
with coefficients
$h_{m+1}$
with coefficients
![]() $\unicode[STIX]{x1D719}(z_{1},\ldots ,z_{m};h_{1},\ldots ,h_{m})$
. We now define
$\unicode[STIX]{x1D719}(z_{1},\ldots ,z_{m};h_{1},\ldots ,h_{m})$
. We now define
![]() ${\mathcal{T}}_{n,m}$
to be the set of all non-zero polynomials
${\mathcal{T}}_{n,m}$
to be the set of all non-zero polynomials
![]() $\unicode[STIX]{x1D719}\in \mathbb{Z}[z_{1},\ldots ,z_{m},h_{1},\ldots ,h_{m}]$
occurring as coefficients of elements
$\unicode[STIX]{x1D719}\in \mathbb{Z}[z_{1},\ldots ,z_{m},h_{1},\ldots ,h_{m}]$
occurring as coefficients of elements
![]() $\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
in this way. Note in particular that since the polynomial (4.1) is not identically zero, it is evident that each set
$\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
in this way. Note in particular that since the polynomial (4.1) is not identically zero, it is evident that each set
![]() ${\mathcal{T}}_{n,m}$
is non-empty.
${\mathcal{T}}_{n,m}$
is non-empty.
This classification of coefficients yields a consequence of Lemma 4.1 of utility to us in §6.
Lemma 4.2. Let
![]() $m$
and
$m$
and
![]() $n$
be natural numbers with
$n$
be natural numbers with
![]() $1\leqslant m\leqslant n\leqslant t$
. Suppose that
$1\leqslant m\leqslant n\leqslant t$
. Suppose that
![]() $z_{i}$
and
$z_{i}$
and
![]() $h_{i}$
are fixed integers for
$h_{i}$
are fixed integers for
![]() $1\leqslant i\leqslant m$
with
$1\leqslant i\leqslant m$
with
![]() $1\leqslant z_{i}\leqslant X$
and
$1\leqslant z_{i}\leqslant X$
and
![]() $|h_{i}|\leqslant X^{r}$
. Suppose also that there exists
$|h_{i}|\leqslant X^{r}$
. Suppose also that there exists
![]() $\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
having the property that
$\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
having the property that
Then the number
![]() $N_{m}(X)$
of integral solutions of the system of equations
$N_{m}(X)$
of integral solutions of the system of equations
with
![]() $1\leqslant z_{m+1}\leqslant X$
and
$1\leqslant z_{m+1}\leqslant X$
and
![]() $|h_{m+1}|\leqslant X^{r}$
, satisfies
$|h_{m+1}|\leqslant X^{r}$
, satisfies
![]() $N_{m}(X)\ll X^{r}$
.
$N_{m}(X)\ll X^{r}$
.
Proof. It follows from the iterative definition of the sets
![]() ${\mathcal{T}}_{n,m}$
that any element
${\mathcal{T}}_{n,m}$
that any element
![]() $\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
occurs as a coefficient polynomial of an element
$\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
occurs as a coefficient polynomial of an element
![]() $\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
, when viewed as a polynomial in
$\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
, when viewed as a polynomial in
![]() $h_{m+1}$
and
$h_{m+1}$
and
![]() $z_{m+1}$
. Fixing any one such polynomial
$z_{m+1}$
. Fixing any one such polynomial
![]() $\unicode[STIX]{x1D713}$
, we find that for the fixed choice of
$\unicode[STIX]{x1D713}$
, we find that for the fixed choice of
![]() $z_{1},\ldots ,z_{m},h_{1},\ldots ,h_{m}$
presented by the hypotheses of the lemma, the polynomial
$z_{1},\ldots ,z_{m},h_{1},\ldots ,h_{m}$
presented by the hypotheses of the lemma, the polynomial
![]() $\unicode[STIX]{x1D713}(\mathbf{z};\mathbf{h})$
is a non-trivial polynomial in
$\unicode[STIX]{x1D713}(\mathbf{z};\mathbf{h})$
is a non-trivial polynomial in
![]() $z_{m+1}$
,
$z_{m+1}$
,
![]() $h_{m+1}$
. We therefore conclude from Lemma 4.1 that
$h_{m+1}$
. We therefore conclude from Lemma 4.1 that
![]() $N_{m}(X)\ll X^{r}$
. This completes the proof of the lemma.◻
$N_{m}(X)\ll X^{r}$
. This completes the proof of the lemma.◻
5 Classification of solutions
We now address the classification of the set
![]() ${\mathcal{S}}$
of all solutions of the system of equations
${\mathcal{S}}$
of all solutions of the system of equations
with
![]() $1\leqslant \mathbf{z}\leqslant X$
and
$1\leqslant \mathbf{z}\leqslant X$
and
![]() $|\mathbf{h}|\leqslant X^{r}$
. This we execute in two stages. Our discussion is eased by the use of some non-standard notation. When
$|\mathbf{h}|\leqslant X^{r}$
. This we execute in two stages. Our discussion is eased by the use of some non-standard notation. When
![]() $(i_{1},\ldots ,i_{m})$
is an
$(i_{1},\ldots ,i_{m})$
is an
![]() $m$
-tuple of positive integers with
$m$
-tuple of positive integers with
![]() $1\leqslant i_{1}<\cdots <i_{m}\leqslant 2s$
, we abbreviate
$1\leqslant i_{1}<\cdots <i_{m}\leqslant 2s$
, we abbreviate
![]() $(z_{i_{1}},\ldots ,z_{i_{m}})$
to
$(z_{i_{1}},\ldots ,z_{i_{m}})$
to
![]() $\mathbf{z}_{\mathbf{i}}$
and
$\mathbf{z}_{\mathbf{i}}$
and
![]() $(h_{i_{1}},\ldots ,h_{i_{m}})$
to
$(h_{i_{1}},\ldots ,h_{i_{m}})$
to
![]() $\mathbf{h}_{\mathbf{i}}$
.
$\mathbf{h}_{\mathbf{i}}$
.
In the first stage of our classification, when
![]() $0\leqslant n<s$
, we say that
$0\leqslant n<s$
, we say that
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}$
is of type
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}$
is of type
![]() $S_{n}$
when:
$S_{n}$
when:
-
(i) for all
 $(n+1)$
-tuples
$(n+1)$
-tuples
 $(i_{1},\ldots ,i_{n+1})$
with
$(i_{1},\ldots ,i_{n+1})$
with
 $1\leqslant i_{1}<\cdots <i_{n+1}\leqslant 2s$
, one has and
$1\leqslant i_{1}<\cdots <i_{n+1}\leqslant 2s$
, one has and $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1}(\mathbf{z}_{\mathbf{i}};\mathbf{h}_{\mathbf{i}}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1}(\mathbf{z}_{\mathbf{i}};\mathbf{h}_{\mathbf{i}}))=0;\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{n}(\unicode[STIX]{x1D70E}_{1,n+1}(\mathbf{z}_{\mathbf{i}};\mathbf{h}_{\mathbf{i}}),\ldots ,\unicode[STIX]{x1D70E}_{2n+1,n+1}(\mathbf{z}_{\mathbf{i}};\mathbf{h}_{\mathbf{i}}))=0;\end{eqnarray}$$
-
(ii) for some
 $n$
-tuple
$n$
-tuple
 $(j_{1},\ldots ,j_{n})$
with
$(j_{1},\ldots ,j_{n})$
with
 $1\leqslant j_{1}<\cdots <j_{n}\leqslant 2s$
, one has
$1\leqslant j_{1}<\cdots <j_{n}\leqslant 2s$
, one has  $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{n-1}(\unicode[STIX]{x1D70E}_{1,n}(\mathbf{z}_{\mathbf{j}};\mathbf{h}_{\mathbf{j}}),\ldots ,\unicode[STIX]{x1D70E}_{2n-1,n}(\mathbf{z}_{\mathbf{j}};\mathbf{h}_{\mathbf{j}}))\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{n-1}(\unicode[STIX]{x1D70E}_{1,n}(\mathbf{z}_{\mathbf{j}};\mathbf{h}_{\mathbf{j}}),\ldots ,\unicode[STIX]{x1D70E}_{2n-1,n}(\mathbf{z}_{\mathbf{j}};\mathbf{h}_{\mathbf{j}}))\neq 0.\end{eqnarray}$$
Here, we interpret the condition (ii) to be void when
![]() $n=0$
. Finally, we say that
$n=0$
. Finally, we say that
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}$
is of type
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}$
is of type
![]() $S_{s}$
when the condition (ii) holds with
$S_{s}$
when the condition (ii) holds with
![]() $n=s$
. It follows that every solution
$n=s$
. It follows that every solution
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}$
is of type
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}$
is of type
![]() $S_{n}$
for some index
$S_{n}$
for some index
![]() $n$
with
$n$
with
![]() $0\leqslant n\leqslant s$
. We denote the set of all solutions of type
$0\leqslant n\leqslant s$
. We denote the set of all solutions of type
![]() $S_{n}$
by
$S_{n}$
by
![]() ${\mathcal{S}}_{n}$
.
${\mathcal{S}}_{n}$
.
In the second stage of our classification, when
![]() $1\leqslant n<s$
we subdivide the solutions
$1\leqslant n<s$
we subdivide the solutions
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n}$
as follows. When
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n}$
as follows. When
![]() $0\leqslant m\leqslant n$
, we say that a solution
$0\leqslant m\leqslant n$
, we say that a solution
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n}$
is of type
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n}$
is of type
![]() $T_{n,m}$
when condition (ii) holds for the
$T_{n,m}$
when condition (ii) holds for the
![]() $n$
-tuple
$n$
-tuple
![]() $\mathbf{j}$
, and:
$\mathbf{j}$
, and:
-
(iii) for all
 $(m+1)$
-tuples
$(m+1)$
-tuples
 $(i_{1},\ldots ,i_{m+1})$
with
$(i_{1},\ldots ,i_{m+1})$
with
 $1\leqslant i_{1}<\cdots <i_{m+1}\leqslant 2s$
and
$1\leqslant i_{1}<\cdots <i_{m+1}\leqslant 2s$
and
 $i_{l}\not \in \{j_{1},\ldots ,j_{n}\}\;(1\leqslant l\leqslant m+1)$
, and for all
$i_{l}\not \in \{j_{1},\ldots ,j_{n}\}\;(1\leqslant l\leqslant m+1)$
, and for all
 $\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
, one has
$\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
, one has
 $\unicode[STIX]{x1D713}(\mathbf{z}_{\mathbf{i}};\mathbf{h}_{\mathbf{i}})=0$
; and
$\unicode[STIX]{x1D713}(\mathbf{z}_{\mathbf{i}};\mathbf{h}_{\mathbf{i}})=0$
; and
-
(iv) for some
 $m$
-tuple
$m$
-tuple
 $(\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m})$
with
$(\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m})$
with
 $1\leqslant \unicode[STIX]{x1D704}_{1}<\cdots <\unicode[STIX]{x1D704}_{m}\leqslant 2s$
and
$1\leqslant \unicode[STIX]{x1D704}_{1}<\cdots <\unicode[STIX]{x1D704}_{m}\leqslant 2s$
and
 $\unicode[STIX]{x1D704}_{l}\not \in \{j_{1},\ldots ,j_{n}\}\;(1\leqslant l\leqslant m)$
, and for some
$\unicode[STIX]{x1D704}_{l}\not \in \{j_{1},\ldots ,j_{n}\}\;(1\leqslant l\leqslant m)$
, and for some
 $\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
, one has
$\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
, one has
 $\unicode[STIX]{x1D719}(\mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}};\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}})\neq 0$
.
$\unicode[STIX]{x1D719}(\mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}};\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}})\neq 0$
.
Here, we interpret the condition (iv) to be void when
![]() $m=0$
. It follows that whenever
$m=0$
. It follows that whenever
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n}$
with
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n}$
with
![]() $1\leqslant n<s$
, then it is of type
$1\leqslant n<s$
, then it is of type
![]() $T_{n,m}$
for some index
$T_{n,m}$
for some index
![]() $m$
with
$m$
with
![]() $0\leqslant m\leqslant n$
. As before, we introduce the notation
$0\leqslant m\leqslant n$
. As before, we introduce the notation
![]() ${\mathcal{S}}_{n,m}$
to denote the set of all solutions of type
${\mathcal{S}}_{n,m}$
to denote the set of all solutions of type
![]() $T_{n,m}$
. We thus have the decomposition
$T_{n,m}$
. We thus have the decomposition
6 A divisor estimate
Having enunciated our classification of solutions in the previous section, we are equipped to estimate the number of solutions of the system (5.1) with
![]() $1\leqslant \mathbf{z}\leqslant X$
and
$1\leqslant \mathbf{z}\leqslant X$
and
![]() $|\mathbf{h}|\leqslant X^{r}$
. This will establish Theorem 2.1, since by discarding superfluous equations if necessary, we may always suppose that
$|\mathbf{h}|\leqslant X^{r}$
. This will establish Theorem 2.1, since by discarding superfluous equations if necessary, we may always suppose that
![]() $t=2s-1$
. Before embarking on the main argument, we establish a simple auxiliary result.
$t=2s-1$
. Before embarking on the main argument, we establish a simple auxiliary result.
Lemma 6.1. Suppose that
![]() $f\in \mathbb{Z}[x]$
is a polynomial of degree
$f\in \mathbb{Z}[x]$
is a polynomial of degree
![]() $k\geqslant 1$
. Let
$k\geqslant 1$
. Let
![]() $u$
be an integer with
$u$
be an integer with
![]() $1\leqslant u\leqslant k$
, and let
$1\leqslant u\leqslant k$
, and let
![]() $h_{i}$
and
$h_{i}$
and
![]() $a_{i}$
be fixed integers for
$a_{i}$
be fixed integers for
![]() $1\leqslant i\leqslant u$
with
$1\leqslant i\leqslant u$
with
![]() $\mathbf{h}\neq \mathbf{0}$
and
$\mathbf{h}\neq \mathbf{0}$
and
![]() $a_{i}\neq a_{j}$
$a_{i}\neq a_{j}$
![]() $(1\leqslant i<j\leqslant u)$
. Then for any integer
$(1\leqslant i<j\leqslant u)$
. Then for any integer
![]() $n$
, the equation
$n$
, the equation
has at most
![]() $k$
solutions in
$k$
solutions in
![]() $z$
.
$z$
.
Proof. It suffices to show that the polynomial in
![]() $z$
on the left-hand side of (6.1) has positive degree. We therefore assume the opposite and seek a contradiction. Suppose that
$z$
on the left-hand side of (6.1) has positive degree. We therefore assume the opposite and seek a contradiction. Suppose that
![]() $f$
is given by
$f$
is given by
where
![]() $c_{k}\neq 0$
. The polynomial on the left-hand side of (6.1) takes the shape
$c_{k}\neq 0$
. The polynomial on the left-hand side of (6.1) takes the shape
with
In particular, we see directly that
![]() $d_{k}$
can vanish only if
$d_{k}$
can vanish only if
![]() $h_{1}+\cdots +h_{u}=0$
. Let
$h_{1}+\cdots +h_{u}=0$
. Let
![]() $i$
be a positive integer with
$i$
be a positive integer with
![]() $i<k$
, and suppose that one has
$i<k$
, and suppose that one has
for all integers
![]() $j$
with
$j$
with
![]() $i<j\leqslant k$
. Then the vanishing of
$i<j\leqslant k$
. Then the vanishing of
![]() $d_{i}$
implies that (6.2) holds also for
$d_{i}$
implies that (6.2) holds also for
![]() $j=i$
. Proceeding inductively in this way, we deduce that (6.2) is satisfied for the entire range
$j=i$
. Proceeding inductively in this way, we deduce that (6.2) is satisfied for the entire range
![]() $1\leqslant j\leqslant k$
. Restricting attention to the system of equations with indices
$1\leqslant j\leqslant k$
. Restricting attention to the system of equations with indices
![]() $k-u+1\leqslant j\leqslant k$
, we find that this system of equations can hold simultaneously only when either
$k-u+1\leqslant j\leqslant k$
, we find that this system of equations can hold simultaneously only when either
![]() $\mathbf{h}=\mathbf{0}$
, or else
$\mathbf{h}=\mathbf{0}$
, or else
In the latter case, one has
![]() $a_{i}=a_{j}$
for some indices
$a_{i}=a_{j}$
for some indices
![]() $i$
and
$i$
and
![]() $j$
with
$j$
with
![]() $1\leqslant i<j\leqslant u$
. Both these cases are excluded by the hypotheses of the statement of the lemma, so the system of equations (6.2) cannot hold for all
$1\leqslant i<j\leqslant u$
. Both these cases are excluded by the hypotheses of the statement of the lemma, so the system of equations (6.2) cannot hold for all
![]() $1\leqslant j\leqslant k$
, and hence the polynomial
$1\leqslant j\leqslant k$
, and hence the polynomial
![]() $F$
is non-trivial of positive degree. Consequently, the equation (6.1) has at most
$F$
is non-trivial of positive degree. Consequently, the equation (6.1) has at most
![]() $\text{deg}(F)\leqslant k$
solutions in
$\text{deg}(F)\leqslant k$
solutions in
![]() $z$
.◻
$z$
.◻
The proof of Theorem 2.1.
We begin by examining the solutions of (5.1) of type
![]() $S_{0}$
, recalling that
$S_{0}$
, recalling that
![]() $1\leqslant \mathbf{z}\leqslant X$
and
$1\leqslant \mathbf{z}\leqslant X$
and
![]() $|\mathbf{h}|\leqslant X^{r}$
. When
$|\mathbf{h}|\leqslant X^{r}$
. When
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{0}$
, one has
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{0}$
, one has
![]() $h_{i}f_{1}(z_{i})=0$
for
$h_{i}f_{1}(z_{i})=0$
for
![]() $1\leqslant i\leqslant 2s$
. Suppose that the indices
$1\leqslant i\leqslant 2s$
. Suppose that the indices
![]() $i$
for which
$i$
for which
![]() $h_{i}=0$
are
$h_{i}=0$
are
![]() $i_{1},\ldots ,i_{a}$
, and the indices
$i_{1},\ldots ,i_{a}$
, and the indices
![]() $j$
for which
$j$
for which
![]() $h_{j}\neq 0$
are
$h_{j}\neq 0$
are
![]() $j_{1},\ldots ,j_{b}$
. In particular, one has
$j_{1},\ldots ,j_{b}$
. In particular, one has
![]() $a+b=2s$
. By relabelling variables, if necessary, there is no loss of generality in supposing that
$a+b=2s$
. By relabelling variables, if necessary, there is no loss of generality in supposing that
![]() $\mathbf{j}=(1,\ldots ,b)$
and
$\mathbf{j}=(1,\ldots ,b)$
and
![]() $\mathbf{i}=(b+1,\ldots ,2s)$
. There are
$\mathbf{i}=(b+1,\ldots ,2s)$
. There are
![]() $O(X^{2s-b})$
possible choices for
$O(X^{2s-b})$
possible choices for
![]() $h_{i}$
and
$h_{i}$
and
![]() $z_{i}$
with
$z_{i}$
with
![]() $b+1\leqslant i\leqslant 2s$
, since
$b+1\leqslant i\leqslant 2s$
, since
![]() $h_{i}=0$
for these indices
$h_{i}=0$
for these indices
![]() $i$
. Meanwhile, for
$i$
. Meanwhile, for
![]() $1\leqslant j\leqslant b$
, one has
$1\leqslant j\leqslant b$
, one has
![]() $f_{1}(z_{j})=0$
, and so there are at most
$f_{1}(z_{j})=0$
, and so there are at most
![]() $k_{1}$
possible choices for
$k_{1}$
possible choices for
![]() $z_{j}$
. For each fixed such choice, since the polynomials
$z_{j}$
. For each fixed such choice, since the polynomials
![]() $f_{1},\ldots ,f_{t}$
are well-conditioned, we find that
$f_{1},\ldots ,f_{t}$
are well-conditioned, we find that
![]() $f_{l}(z_{j})\neq 0$
for some index
$f_{l}(z_{j})\neq 0$
for some index
![]() $l$
with
$l$
with
![]() $2\leqslant l\leqslant t$
. Thus, the variables
$2\leqslant l\leqslant t$
. Thus, the variables
![]() $h_{1},\ldots ,h_{b}$
satisfy a system of
$h_{1},\ldots ,h_{b}$
satisfy a system of
![]() $t$
linear equations in which there are non-vanishing coefficients. We deduce that when
$t$
linear equations in which there are non-vanishing coefficients. We deduce that when
![]() $b\geqslant 1$
, there are
$b\geqslant 1$
, there are
![]() $O((X^{r})^{b-1})$
possible choices for
$O((X^{r})^{b-1})$
possible choices for
![]() $h_{j}$
and
$h_{j}$
and
![]() $z_{j}$
with
$z_{j}$
with
![]() $1\leqslant j\leqslant b$
. Finally, combining these estimates for all possible choices of
$1\leqslant j\leqslant b$
. Finally, combining these estimates for all possible choices of
![]() $\mathbf{i}$
and
$\mathbf{i}$
and
![]() $\mathbf{j}$
, we discern that
$\mathbf{j}$
, we discern that
Next we consider the solutions of (5.1) of type
![]() $S_{s}$
. When
$S_{s}$
. When
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{s}$
, there is an
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{s}$
, there is an
![]() $s$
-tuple
$s$
-tuple
![]() $\mathbf{i}$
with
$\mathbf{i}$
with
![]() $1\leqslant i_{1}<\cdots <i_{s}\leqslant 2s$
for which one has
$1\leqslant i_{1}<\cdots <i_{s}\leqslant 2s$
for which one has
Write
![]() $\mathbf{i}^{\prime }$
for the
$\mathbf{i}^{\prime }$
for the
![]() $s$
-tuple
$s$
-tuple
![]() $(i_{1}^{\prime },\ldots ,i_{s}^{\prime })$
with
$(i_{1}^{\prime },\ldots ,i_{s}^{\prime })$
with
![]() $1\leqslant i_{1}^{\prime }<\cdots <i_{s}^{\prime }\leqslant 2s$
for which
$1\leqslant i_{1}^{\prime }<\cdots <i_{s}^{\prime }\leqslant 2s$
for which
It follows from (5.1) that
![]() $\unicode[STIX]{x1D70E}_{j,s}(\mathbf{z}_{\mathbf{i}};\mathbf{h}_{\mathbf{i}})=\unicode[STIX]{x1D70E}_{j,s}(\mathbf{z}_{\mathbf{i}^{\prime }};-\mathbf{h}_{\mathbf{i}^{\prime }})\;(1\leqslant j\leqslant 2s-1)$
, and hence there is a non-zero integer
$\unicode[STIX]{x1D70E}_{j,s}(\mathbf{z}_{\mathbf{i}};\mathbf{h}_{\mathbf{i}})=\unicode[STIX]{x1D70E}_{j,s}(\mathbf{z}_{\mathbf{i}^{\prime }};-\mathbf{h}_{\mathbf{i}^{\prime }})\;(1\leqslant j\leqslant 2s-1)$
, and hence there is a non-zero integer
![]() $N=N(\mathbf{z}_{\mathbf{i}^{\prime }};\mathbf{h}_{\mathbf{i}^{\prime }})$
for which
$N=N(\mathbf{z}_{\mathbf{i}^{\prime }};\mathbf{h}_{\mathbf{i}^{\prime }})$
for which
and
By relabelling variables, if necessary, there is no loss of generality in supposing that
![]() $\mathbf{i}=(1,2,\ldots ,s)$
and
$\mathbf{i}=(1,2,\ldots ,s)$
and
![]() $\mathbf{i}^{\prime }=(s+1,s+2,\ldots ,2s)$
.
$\mathbf{i}^{\prime }=(s+1,s+2,\ldots ,2s)$
.
Fix any one of the
![]() $O(X^{(r+1)s})$
possible choices for
$O(X^{(r+1)s})$
possible choices for
![]() $\mathbf{z}_{\mathbf{i}^{\prime }}$
,
$\mathbf{z}_{\mathbf{i}^{\prime }}$
,
![]() $\mathbf{h}_{\mathbf{i}^{\prime }}$
with
$\mathbf{h}_{\mathbf{i}^{\prime }}$
with
![]() $1\leqslant \mathbf{z}_{\mathbf{i}^{\prime }}\leqslant X$
,
$1\leqslant \mathbf{z}_{\mathbf{i}^{\prime }}\leqslant X$
,
![]() $|\mathbf{h}_{\mathbf{i}^{\prime }}|\leqslant X^{r}$
, and satisfying (6.4). Then we infer from Lemma 3.2 that
$|\mathbf{h}_{\mathbf{i}^{\prime }}|\leqslant X^{r}$
, and satisfying (6.4). Then we infer from Lemma 3.2 that
Moreover, one has
![]() $N(\mathbf{z}_{\mathbf{i}^{\prime }};\mathbf{h}_{\mathbf{i}^{\prime }})\neq 0$
. Since the latter integer is fixed, we see by means of an elementary divisor function estimate that there are
$N(\mathbf{z}_{\mathbf{i}^{\prime }};\mathbf{h}_{\mathbf{i}^{\prime }})\neq 0$
. Since the latter integer is fixed, we see by means of an elementary divisor function estimate that there are
![]() $O(X^{\unicode[STIX]{x1D700}})$
possible choices for
$O(X^{\unicode[STIX]{x1D700}})$
possible choices for
![]() $h_{1},\ldots ,h_{s}$
and integers
$h_{1},\ldots ,h_{s}$
and integers
![]() $a_{2},\ldots ,a_{s}$
equipped with the property that
$a_{2},\ldots ,a_{s}$
equipped with the property that
![]() $z_{i}=z_{1}+a_{i}\;(2\leqslant i\leqslant s)$
. With the exception of the undetermined variable
$z_{i}=z_{1}+a_{i}\;(2\leqslant i\leqslant s)$
. With the exception of the undetermined variable
![]() $z_{1}$
, it follows that there are at most
$z_{1}$
, it follows that there are at most
![]() $O(X^{(r+1)s+\unicode[STIX]{x1D700}})$
possible choices for all the variables in question. However, the integer
$O(X^{(r+1)s+\unicode[STIX]{x1D700}})$
possible choices for all the variables in question. However, the integer
![]() $z_{1}$
satisfies the system of equations
$z_{1}$
satisfies the system of equations
in which
![]() $h_{i}$
,
$h_{i}$
,
![]() $a_{i}$
and
$a_{i}$
and
![]() $n_{j}$
are all fixed for all indices
$n_{j}$
are all fixed for all indices
![]() $i$
and
$i$
and
![]() $j$
. Consider the polynomial with index
$j$
. Consider the polynomial with index
![]() $j=1$
of largest degree
$j=1$
of largest degree
![]() $k_{1}\geqslant 2s-2$
. If
$k_{1}\geqslant 2s-2$
. If
![]() $a_{i}$
is zero for any index
$a_{i}$
is zero for any index
![]() $i$
, then we have
$i$
, then we have
![]() $z_{1}=z_{i}$
. Meanwhile, if
$z_{1}=z_{i}$
. Meanwhile, if
![]() $a_{i}=a_{j}$
for any indices
$a_{i}=a_{j}$
for any indices
![]() $i$
and
$i$
and
![]() $j$
with
$j$
with
![]() $2\leqslant i<j\leqslant s$
, one sees that
$2\leqslant i<j\leqslant s$
, one sees that
![]() $z_{i}=z_{j}$
. Consequently, in either of these scenarios, and also in the situation with
$z_{i}=z_{j}$
. Consequently, in either of these scenarios, and also in the situation with
![]() $\mathbf{h}=\mathbf{0}$
, one finds via (6.5) that
$\mathbf{h}=\mathbf{0}$
, one finds via (6.5) that
![]() $N(\mathbf{z}_{\mathbf{i}^{\prime }};\mathbf{h}_{\mathbf{i}^{\prime }})=0$
, contradicting our assumption that
$N(\mathbf{z}_{\mathbf{i}^{\prime }};\mathbf{h}_{\mathbf{i}^{\prime }})=0$
, contradicting our assumption that
![]() $N(\mathbf{z}_{\mathbf{i}^{\prime }};\mathbf{h}_{\mathbf{i}^{\prime }})\neq 0$
. We may thus safely assume that the conditions of Lemma 6.1 are satisfied for the polynomial
$N(\mathbf{z}_{\mathbf{i}^{\prime }};\mathbf{h}_{\mathbf{i}^{\prime }})\neq 0$
. We may thus safely assume that the conditions of Lemma 6.1 are satisfied for the polynomial
![]() $f_{1}$
with
$f_{1}$
with
![]() $a_{1}=0$
. By the conclusion of the lemma, it follows that there are at most
$a_{1}=0$
. By the conclusion of the lemma, it follows that there are at most
![]() $k_{1}$
choices for
$k_{1}$
choices for
![]() $z_{1}$
satisfying (6.6), and hence
$z_{1}$
satisfying (6.6), and hence
Next we consider the set
![]() ${\mathcal{S}}_{n,m}$
for a given pair of indices
${\mathcal{S}}_{n,m}$
for a given pair of indices
![]() $n$
and
$n$
and
![]() $m$
with
$m$
with
![]() $1\leqslant n<s$
and
$1\leqslant n<s$
and
![]() $0\leqslant m\leqslant n$
. For any
$0\leqslant m\leqslant n$
. For any
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n,m}$
, condition (ii) holds for some
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n,m}$
, condition (ii) holds for some
![]() $n$
-tuple
$n$
-tuple
![]() $\mathbf{j}$
. By relabelling variables, if necessary, we may suppose that
$\mathbf{j}$
. By relabelling variables, if necessary, we may suppose that
![]() $\mathbf{j}=(1,\ldots ,n)$
. Write
$\mathbf{j}=(1,\ldots ,n)$
. Write
![]() $\mathbf{j}^{\prime }$
for the
$\mathbf{j}^{\prime }$
for the
![]() $(2s-n)$
-tuple
$(2s-n)$
-tuple
![]() $(n+1,\ldots ,2s)$
. Then given any one fixed choice of the variables
$(n+1,\ldots ,2s)$
. Then given any one fixed choice of the variables
![]() $\mathbf{z}_{\mathbf{j}^{\prime }}$
,
$\mathbf{z}_{\mathbf{j}^{\prime }}$
,
![]() $\mathbf{h}_{\mathbf{j}^{\prime }}$
, we have
$\mathbf{h}_{\mathbf{j}^{\prime }}$
, we have
Thus, there is a fixed non-zero integer
![]() $N$
with the property that
$N$
with the property that
and we deduce from Lemma 3.2 that
From here, the argument applied above in the case
![]() $n=s$
may be employed mutatis mutandis to conclude that there are
$n=s$
may be employed mutatis mutandis to conclude that there are
![]() $O(X^{\unicode[STIX]{x1D700}})$
possible choices for
$O(X^{\unicode[STIX]{x1D700}})$
possible choices for
![]() $h_{1},\ldots ,h_{n}$
,
$h_{1},\ldots ,h_{n}$
,
![]() $z_{1}-z_{2},\ldots ,z_{1}-z_{n}$
. If we put
$z_{1}-z_{2},\ldots ,z_{1}-z_{n}$
. If we put
![]() $a_{i}=z_{i}-z_{1}\;(2\leqslant i\leqslant n)$
and
$a_{i}=z_{i}-z_{1}\;(2\leqslant i\leqslant n)$
and
![]() $a_{1}=0$
, then we find just as in our earlier analysis that
$a_{1}=0$
, then we find just as in our earlier analysis that
![]() $z_{1}$
satisfies a non-trivial polynomial equation of degree at most
$z_{1}$
satisfies a non-trivial polynomial equation of degree at most
![]() $k_{1}$
, whence there are at most
$k_{1}$
, whence there are at most
![]() $k_{1}$
choices for
$k_{1}$
choices for
![]() $z_{1}$
. We therefore conclude that, given any one fixed choice of
$z_{1}$
. We therefore conclude that, given any one fixed choice of
![]() $\mathbf{z}_{\mathbf{j}^{\prime }},\mathbf{h}_{\mathbf{j}^{\prime }}$
, the number of choices for
$\mathbf{z}_{\mathbf{j}^{\prime }},\mathbf{h}_{\mathbf{j}^{\prime }}$
, the number of choices for
![]() $\mathbf{z}_{\mathbf{j}},\mathbf{h}_{\mathbf{j}}$
is
$\mathbf{z}_{\mathbf{j}},\mathbf{h}_{\mathbf{j}}$
is
![]() $O(X^{\unicode[STIX]{x1D700}})$
.
$O(X^{\unicode[STIX]{x1D700}})$
.
It thus remains to count the number of choices for
![]() $\mathbf{z}_{\mathbf{j}^{\prime }}$
and
$\mathbf{z}_{\mathbf{j}^{\prime }}$
and
![]() $\mathbf{h}_{\mathbf{j}^{\prime }}$
. Note in particular that, since
$\mathbf{h}_{\mathbf{j}^{\prime }}$
. Note in particular that, since
![]() $(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n,m}$
, we have the additional information that conditions (iii) and (iv) are satisfied. We may therefore suppose that there exists some
$(\mathbf{z},\mathbf{h})\in {\mathcal{S}}_{n,m}$
, we have the additional information that conditions (iii) and (iv) are satisfied. We may therefore suppose that there exists some
![]() $\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
, and some
$\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
, and some
![]() $m$
-tuple
$m$
-tuple
![]() $(\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m})$
with
$(\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m})$
with
![]() $n+1\leqslant \unicode[STIX]{x1D704}_{1}<\cdots <\unicode[STIX]{x1D704}_{m}\leqslant 2s$
, for which
$n+1\leqslant \unicode[STIX]{x1D704}_{1}<\cdots <\unicode[STIX]{x1D704}_{m}\leqslant 2s$
, for which
With a fixed choice of
![]() $\boldsymbol{\unicode[STIX]{x1D704}}$
, we may suppose further that for all
$\boldsymbol{\unicode[STIX]{x1D704}}$
, we may suppose further that for all
![]() $i$
satisfying
$i$
satisfying
![]() $n+1\leqslant i\leqslant 2s$
and
$n+1\leqslant i\leqslant 2s$
and
![]() $i\not \in \{\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m}\}$
, and for all
$i\not \in \{\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m}\}$
, and for all
![]() $\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
, one has
$\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
, one has
Given any such
![]() $\boldsymbol{\unicode[STIX]{x1D704}}$
and
$\boldsymbol{\unicode[STIX]{x1D704}}$
and
![]() $\unicode[STIX]{x1D719}$
, there are
$\unicode[STIX]{x1D719}$
, there are
![]() $O(X^{(r+1)m})$
possible choices for
$O(X^{(r+1)m})$
possible choices for
![]() $\mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}},\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}}$
, with
$\mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}},\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}}$
, with
![]() $1\leqslant \mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}}\leqslant X$
and
$1\leqslant \mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}}\leqslant X$
and
![]() $|\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}}|\leqslant X^{r}$
, satisfying (6.8). We claim that for any fixed such choice, the number of possible choices for the integers
$|\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}}|\leqslant X^{r}$
, satisfying (6.8). We claim that for any fixed such choice, the number of possible choices for the integers
![]() $z_{i}$
and
$z_{i}$
and
![]() $h_{i}$
with
$h_{i}$
with
![]() $n+1\leqslant i\leqslant 2s$
and
$n+1\leqslant i\leqslant 2s$
and
![]() $i\not \in \{\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m}\}$
is
$i\not \in \{\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m}\}$
is
![]() $O((X^{r})^{2s-n-m})$
. In order to confirm this claim, observe that there is a polynomial
$O((X^{r})^{2s-n-m})$
. In order to confirm this claim, observe that there is a polynomial
![]() $\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
having the property that some coefficient of
$\unicode[STIX]{x1D713}\in {\mathcal{T}}_{n,m+1}$
having the property that some coefficient of
![]() $\unicode[STIX]{x1D713}(z_{1},\ldots ,z_{m+1};h_{1},\ldots ,h_{m+1})$
, considered as a polynomial in
$\unicode[STIX]{x1D713}(z_{1},\ldots ,z_{m+1};h_{1},\ldots ,h_{m+1})$
, considered as a polynomial in
![]() $z_{m+1}$
and
$z_{m+1}$
and
![]() $h_{m+1}$
, is equal to
$h_{m+1}$
, is equal to
![]() $\unicode[STIX]{x1D719}(z_{1},\ldots ,z_{m};h_{1},\ldots ,h_{m})$
. It then follows from (6.8) that the equation (6.9) is a non-trivial polynomial equation in
$\unicode[STIX]{x1D719}(z_{1},\ldots ,z_{m};h_{1},\ldots ,h_{m})$
. It then follows from (6.8) that the equation (6.9) is a non-trivial polynomial equation in
![]() $z_{i}$
and
$z_{i}$
and
![]() $h_{i}$
. We therefore deduce from Lemma 4.2 that for each fixed choice of
$h_{i}$
. We therefore deduce from Lemma 4.2 that for each fixed choice of
![]() $\mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}}$
and
$\mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}}$
and
![]() $\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}}$
under consideration, and for each
$\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}}$
under consideration, and for each
![]() $i$
with
$i$
with
![]() $n+1\leqslant i\leqslant 2s$
and
$n+1\leqslant i\leqslant 2s$
and
![]() $i\not \in \{\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m}\}$
, there are
$i\not \in \{\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{m}\}$
, there are
![]() $O(X^{r})$
possible choices for
$O(X^{r})$
possible choices for
![]() $z_{i}$
and
$z_{i}$
and
![]() $h_{i}$
satisfying (6.9). Thus we infer that there are
$h_{i}$
satisfying (6.9). Thus we infer that there are
![]() $O(X^{r(2s-n-m)})$
possible choices for
$O(X^{r(2s-n-m)})$
possible choices for
![]() $z_{i}$
and
$z_{i}$
and
![]() $h_{i}$
with
$h_{i}$
with
![]() $n+1\leqslant i\leqslant 2s$
for each fixed choice of
$n+1\leqslant i\leqslant 2s$
for each fixed choice of
![]() $\mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}},\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}}$
. Since the number of choices for
$\mathbf{z}_{\boldsymbol{\unicode[STIX]{x1D704}}},\mathbf{h}_{\boldsymbol{\unicode[STIX]{x1D704}}}$
. Since the number of choices for
![]() $\boldsymbol{\unicode[STIX]{x1D704}}$
and
$\boldsymbol{\unicode[STIX]{x1D704}}$
and
![]() $\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
is
$\unicode[STIX]{x1D719}\in {\mathcal{T}}_{n,m}$
is
![]() $O(1)$
, the total number of choices for
$O(1)$
, the total number of choices for
![]() $\mathbf{z}_{\mathbf{j}^{\prime }}$
and
$\mathbf{z}_{\mathbf{j}^{\prime }}$
and
![]() $\mathbf{h}_{\mathbf{j}^{\prime }}$
available to us is
$\mathbf{h}_{\mathbf{j}^{\prime }}$
available to us is
![]() $O(X^{(r+1)m}\cdot X^{r(2s-n-m)})$
. Furthermore, our discussion above showed that for each fixed such choice of
$O(X^{(r+1)m}\cdot X^{r(2s-n-m)})$
. Furthermore, our discussion above showed that for each fixed such choice of
![]() $\mathbf{z}_{\mathbf{j}^{\prime }}$
,
$\mathbf{z}_{\mathbf{j}^{\prime }}$
,
![]() $\mathbf{h}_{\mathbf{j}^{\prime }}$
, the number of possible choices for
$\mathbf{h}_{\mathbf{j}^{\prime }}$
, the number of possible choices for
![]() $\mathbf{z}_{\mathbf{j}},\mathbf{h}_{\mathbf{j}}$
is
$\mathbf{z}_{\mathbf{j}},\mathbf{h}_{\mathbf{j}}$
is
![]() $O(X^{\unicode[STIX]{x1D700}})$
. Thus altogether we conclude that
$O(X^{\unicode[STIX]{x1D700}})$
. Thus altogether we conclude that
By combining our estimates (6.3), (6.7) and (6.10) via (5.2), we discern that
and the conclusion of Theorem 2.1 follows. ◻
7 The proof of Theorems 1.1 and 1.2
Our preparations now complete, we establish the mean value estimates recorded in Theorems 1.1 and 1.2. Let
![]() $X$
be a large positive number, and suppose that
$X$
be a large positive number, and suppose that
![]() $s$
and
$s$
and
![]() $k$
are natural numbers with
$k$
are natural numbers with
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $1\leqslant s\leqslant (k^{2}-1)/2$
. We define the exponential sum
$1\leqslant s\leqslant (k^{2}-1)/2$
. We define the exponential sum
![]() $\mathfrak{g}_{r}(\boldsymbol{\unicode[STIX]{x1D6FC}};X)$
by putting
$\mathfrak{g}_{r}(\boldsymbol{\unicode[STIX]{x1D6FC}};X)$
by putting
Also, when
![]() $1\leqslant d\leqslant k$
, we put
$1\leqslant d\leqslant k$
, we put
Then, with the standard notation associated with Vinogradov’s mean value theorem in mind, we put
We note that the main conjecture in Vinogradov’s mean value theorem is now known to hold for all degrees. This is a consequence of work of the second author for degree
![]() $3$
, and for degrees exceeding
$3$
, and for degrees exceeding
![]() $3$
it follows from the work of Bourgain, Demeter and Guth (see [Reference Wooley9, Theorem 1.1] and [Reference Bourgain, Demeter and Guth1, Theorem 1.1]). Thus, one has
$3$
it follows from the work of Bourgain, Demeter and Guth (see [Reference Wooley9, Theorem 1.1] and [Reference Bourgain, Demeter and Guth1, Theorem 1.1]). Thus, one has
In addition, one finds via orthogonality that for each integer
![]() $\unicode[STIX]{x1D705}$
, one has
$\unicode[STIX]{x1D705}$
, one has
where
![]() $f_{j}(z)=z^{k-r+1-j}\;(1\leqslant j\leqslant k-r+1)$
.
$f_{j}(z)=z^{k-r+1-j}\;(1\leqslant j\leqslant k-r+1)$
.
Lemma 7.1. When
![]() $s$
is a natural number, one has
$s$
is a natural number, one has
Proof. Define
![]() $\unicode[STIX]{x1D6FF}_{j}$
to be
$\unicode[STIX]{x1D6FF}_{j}$
to be
![]() $1$
when
$1$
when
![]() $j=r$
, and
$j=r$
, and
![]() $0$
otherwise. We start by noting that the mean value
$0$
otherwise. We start by noting that the mean value
![]() $I_{s,k,r}(X)$
counts the number of integral solutions of the system of equations
$I_{s,k,r}(X)$
counts the number of integral solutions of the system of equations
with
![]() $1\leqslant x_{i},y_{i}\leqslant X\;(1\leqslant i\leqslant s)$
and
$1\leqslant x_{i},y_{i}\leqslant X\;(1\leqslant i\leqslant s)$
and
![]() $|h|\leqslant sX^{r}$
. We remark that the constraint on
$|h|\leqslant sX^{r}$
. We remark that the constraint on
imposed by the equation of degree
![]() $r$
in (7.4) is void, since the range for
$r$
in (7.4) is void, since the range for
![]() $h$
automatically accommodates all possible values of the expression (7.5) within (7.4).
$h$
automatically accommodates all possible values of the expression (7.5) within (7.4).
We next consider the effect of shifting every variable by an integer
![]() $z$
with
$z$
with
![]() $1\leqslant z\leqslant X$
. By the binomial theorem, for any shift
$1\leqslant z\leqslant X$
. By the binomial theorem, for any shift
![]() $z$
, one finds that
$z$
, one finds that
![]() $(\mathbf{x},\mathbf{y})$
is a solution of (7.4) if and only if it is also a solution of the system
$(\mathbf{x},\mathbf{y})$
is a solution of (7.4) if and only if it is also a solution of the system
where
![]() $\unicode[STIX]{x1D714}_{j}$
is
$\unicode[STIX]{x1D714}_{j}$
is
![]() $0$
for
$0$
for
![]() $1\leqslant j<r$
and
$1\leqslant j<r$
and
![]() $\binom{j}{r}$
for
$\binom{j}{r}$
for
![]() $r\leqslant j\leqslant k$
. Thus, for each fixed integer
$r\leqslant j\leqslant k$
. Thus, for each fixed integer
![]() $z$
with
$z$
with
![]() $1\leqslant z\leqslant X$
, the mean value
$1\leqslant z\leqslant X$
, the mean value
![]() $I_{s,k,r}(X)$
is bounded above by the number of integral solutions of the system
$I_{s,k,r}(X)$
is bounded above by the number of integral solutions of the system
with
![]() $1\leqslant \mathbf{u},\mathbf{v}\leqslant 2X$
and
$1\leqslant \mathbf{u},\mathbf{v}\leqslant 2X$
and
![]() $|h|\leqslant sX^{r}$
. On applying orthogonality, we therefore infer that
$|h|\leqslant sX^{r}$
. On applying orthogonality, we therefore infer that
where
The proof of the lemma is completed by reference to (7.1). ◻
The proof of Theorem 1.2.
Let
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $r$
be integers with
$r$
be integers with
![]() $k>r\geqslant 1$
. Also, let
$k>r\geqslant 1$
. Also, let
![]() $\unicode[STIX]{x1D705}$
be a positive integer with
$\unicode[STIX]{x1D705}$
be a positive integer with
![]() $\unicode[STIX]{x1D705}\leqslant (k-r+2)/2$
. Observe that it suffices to restrict attention to the special case
$\unicode[STIX]{x1D705}\leqslant (k-r+2)/2$
. Observe that it suffices to restrict attention to the special case
since one may interpolate via Hölder’s inequality to recover the conclusion of the theorem for smaller values of
![]() $s$
. Put
$s$
. Put
Furthermore, set
so that
![]() $s=\lfloor v+w\rfloor$
. In particular, we have
$s=\lfloor v+w\rfloor$
. In particular, we have
![]() $w\geqslant u$
.
$w\geqslant u$
.
On applying Hölder’s inequality in combination with Lemma 7.1, we find that
where
and
A comparison of (7.7) with (7.2) leads us via (7.3) to the estimate
Meanwhile, by orthogonality, we discern from (7.8) that
![]() $U_{2}$
counts the number of integral solutions of the system of equations
$U_{2}$
counts the number of integral solutions of the system of equations
with
![]() $1\leqslant \mathbf{x},\mathbf{y}\leqslant 2X$
,
$1\leqslant \mathbf{x},\mathbf{y}\leqslant 2X$
,
![]() $1\leqslant \mathbf{z}\leqslant X$
and
$1\leqslant \mathbf{z}\leqslant X$
and
![]() $|\mathbf{h}|\leqslant sX^{r}$
. By interpreting (7.11) through the prism of orthogonality, it follows from (7.2) that the number of available choices for
$|\mathbf{h}|\leqslant sX^{r}$
. By interpreting (7.11) through the prism of orthogonality, it follows from (7.2) that the number of available choices for
![]() $\mathbf{x}$
and
$\mathbf{x}$
and
![]() $\mathbf{y}$
is bounded above by
$\mathbf{y}$
is bounded above by
![]() $J_{r(r-1)/2,r-1}(2X)$
. For each fixed such choice of
$J_{r(r-1)/2,r-1}(2X)$
. For each fixed such choice of
![]() $\mathbf{x}$
and
$\mathbf{x}$
and
![]() $\mathbf{y}$
, it follows from (7.10) via orthogonality and the triangle inequality that the number of available choices for
$\mathbf{y}$
, it follows from (7.10) via orthogonality and the triangle inequality that the number of available choices for
![]() $\mathbf{z}$
and
$\mathbf{z}$
and
![]() $\mathbf{h}$
is at most
$\mathbf{h}$
is at most
![]() $A_{\unicode[STIX]{x1D705},r}(sX;\mathbf{f}\,)$
. Thus we deduce from (7.3) and Theorem 2.1 that
$A_{\unicode[STIX]{x1D705},r}(sX;\mathbf{f}\,)$
. Thus we deduce from (7.3) and Theorem 2.1 that
On substituting (7.9) and (7.12) into (7.6), we infer that
where
This completes the proof of Theorem 1.2. ◻
The proof of Theorem 1.1.
The conclusion of Theorem 1.1 is an immediate consequence of Theorem 1.2 in the special case
![]() $r=1$
. Making use of the notation of the statement of the latter theorem, we note that when
$r=1$
. Making use of the notation of the statement of the latter theorem, we note that when
![]() $k=2l+1$
is odd, one may take
$k=2l+1$
is odd, one may take
![]() $\unicode[STIX]{x1D705}=\lfloor (k+1)/2\rfloor =l+1$
, and we deduce that
$\unicode[STIX]{x1D705}=\lfloor (k+1)/2\rfloor =l+1$
, and we deduce that
![]() $I_{s,k,1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
provided that
$I_{s,k,1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
provided that
![]() $s$
is a natural number not exceeding
$s$
is a natural number not exceeding
Meanwhile, when
![]() $k=2l$
is even, one may instead take
$k=2l$
is even, one may instead take
![]() $\unicode[STIX]{x1D705}=l$
, and the same conclusion holds provided that
$\unicode[STIX]{x1D705}=l$
, and the same conclusion holds provided that
![]() $s$
is a natural number not exceeding
$s$
is a natural number not exceeding
The desired conclusion therefore follows in both cases, and the proof of Theorem 1.1 is complete. ◻
Acknowledgements
Both authors thank the Fields Institute in Toronto for excellent working conditions and support that made this work possible during the Thematic Program on Unlikely Intersections, Heights, and Efficient Congruencing. The work of the first author was supported by the National Science Foundation under Grant No. DMS-1440140 while the author was in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the Spring 2017 semester. The second author’s work was supported by a European Research Council Advanced Grant under the European Union’s Horizon 2020 research and innovation programme via grant agreement No. 695223.