Article contents
FAMILIES OF THUE EQUATIONS ASSOCIATED WITH A RANK ONE SUBGROUP OF THE UNIT GROUP OF A NUMBER FIELD
Published online by Cambridge University Press: 29 November 2017
Abstract
Let 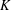 $K$ be an algebraic number field of degree
$K$ be an algebraic number field of degree 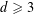 $d\geqslant 3$ ,
$d\geqslant 3$ , 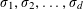 $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\ldots ,\unicode[STIX]{x1D70E}_{d}$ the embeddings of
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\ldots ,\unicode[STIX]{x1D70E}_{d}$ the embeddings of 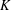 $K$ into
$K$ into 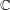 $\mathbb{C}$ ,
$\mathbb{C}$ ,  $\unicode[STIX]{x1D6FC}$ a non-zero element in
$\unicode[STIX]{x1D6FC}$ a non-zero element in 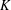 $K$ ,
$K$ , 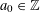 $a_{0}\in \mathbb{Z}$ ,
$a_{0}\in \mathbb{Z}$ , 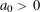 $a_{0}>0$ and
$a_{0}>0$ and 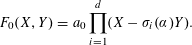 $$\begin{eqnarray}F_{0}(X,Y)=a_{0}\mathop{\prod }_{i=1}^{d}(X-\unicode[STIX]{x1D70E}_{i}(\unicode[STIX]{x1D6FC})Y).\end{eqnarray}$$
$$\begin{eqnarray}F_{0}(X,Y)=a_{0}\mathop{\prod }_{i=1}^{d}(X-\unicode[STIX]{x1D70E}_{i}(\unicode[STIX]{x1D6FC})Y).\end{eqnarray}$$ $\unicode[STIX]{x1D710}$ be a unit in
$\unicode[STIX]{x1D710}$ be a unit in 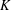 $K$ . For
$K$ . For 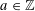 $a\in \mathbb{Z}$ , we twist the binary form
$a\in \mathbb{Z}$ , we twist the binary form 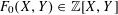 $F_{0}(X,Y)\in \mathbb{Z}[X,Y]$ by the powers
$F_{0}(X,Y)\in \mathbb{Z}[X,Y]$ by the powers 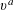 $\unicode[STIX]{x1D710}^{a}$ (
$\unicode[STIX]{x1D710}^{a}$ ( 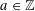 $a\in \mathbb{Z}$ ) of
$a\in \mathbb{Z}$ ) of  $\unicode[STIX]{x1D710}$ by setting
$\unicode[STIX]{x1D710}$ by setting 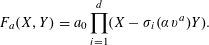 $$\begin{eqnarray}F_{a}(X,Y)=a_{0}\mathop{\prod }_{i=1}^{d}(X-\unicode[STIX]{x1D70E}_{i}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D710}^{a})Y).\end{eqnarray}$$
$$\begin{eqnarray}F_{a}(X,Y)=a_{0}\mathop{\prod }_{i=1}^{d}(X-\unicode[STIX]{x1D70E}_{i}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D710}^{a})Y).\end{eqnarray}$$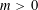 $m>0$ , our main result is an effective upper bound for the size of solutions
$m>0$ , our main result is an effective upper bound for the size of solutions 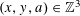 $(x,y,a)\in \mathbb{Z}^{3}$ of the Diophantine inequalities
$(x,y,a)\in \mathbb{Z}^{3}$ of the Diophantine inequalities 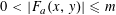 $$\begin{eqnarray}0<|F_{a}(x,y)|\leqslant m\end{eqnarray}$$
$$\begin{eqnarray}0<|F_{a}(x,y)|\leqslant m\end{eqnarray}$$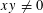 $xy\not =0$ and
$xy\not =0$ and 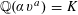 $\mathbb{Q}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D710}^{a})=K$ . Our estimate is explicit in terms of its dependence on
$\mathbb{Q}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D710}^{a})=K$ . Our estimate is explicit in terms of its dependence on 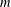 $m$ , the regulator of
$m$ , the regulator of 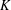 $K$ and the heights of
$K$ and the heights of 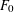 $F_{0}$ and of
$F_{0}$ and of  $\unicode[STIX]{x1D710}$ ; it also involves an effectively computable constant depending only on
$\unicode[STIX]{x1D710}$ ; it also involves an effectively computable constant depending only on 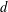 $d$ .
$d$ .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2017
References
- 1
- Cited by

