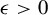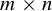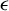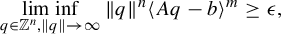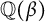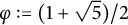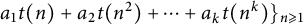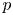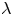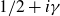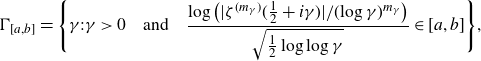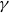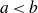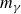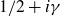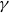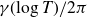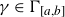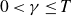Refine listing
Actions for selected content:
237 results in 11Jxx
Dimension estimates for badly approximable affine forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1541-1596
- Print publication:
- May 2025
-
- Article
- Export citation
Zagier–Hoffman’s Conjectures in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 October 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform Diophantine approximation and run-length function in continued fractions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1246-1280
- Print publication:
- April 2025
-
- Article
- Export citation
Poissonian pair correlation for directions in multi-dimensional affine lattices and escape of mass estimates for embedded horospheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 26 April 2024, pp. 218-246
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schmidt games and Cantor winning sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 71-110
- Print publication:
- January 2025
-
- Article
- Export citation
Attractors are not algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1073-1100
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPROXIMATION OF IRRATIONAL NUMBERS BY PAIRS OF INTEGERS FROM A LARGE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 03 April 2024, pp. 439-447
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrepancy of rational points in simple algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 836-877
- Print publication:
- April 2024
-
- Article
- Export citation
WEIERSTRASS ZETA FUNCTIONS AND p-ADIC LINEAR RELATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 234-243
- Print publication:
- October 2024
-
- Article
- Export citation
Linear independence of series related to the Thue–Morse sequence along powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 822-832
- Print publication:
- September 2024
-
- Article
- Export citation
There are at most finitely many singular moduli that are S-units
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 732-770
- Print publication:
- April 2024
-
- Article
- Export citation
The uniform distribution modulo one of certain subsequences of ordinates of zeros of the zeta function
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 01 March 2024, pp. 593-608
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIOPHANTINE TRANSFERENCE PRINCIPLE OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 216-233
- Print publication:
- October 2024
-
- Article
- Export citation
Bracket words along Hardy field sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 14 December 2023, pp. 2621-2648
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR INDEPENDENCE OF VALUES OF THE q-EXPONENTIAL AND RELATED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 453-463
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE EXCEPTIONAL SET OF TRANSCENDENTAL ENTIRE FUNCTIONS IN SEVERAL VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 64-71
- Print publication:
- August 2024
-
- Article
- Export citation
On Thakur’s basis conjecture for multiple zeta values in positive characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 October 2023, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential multiple mixing for commuting automorphisms of a nilmanifold
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1729-1740
- Print publication:
- July 2024
-
- Article
- Export citation
Algebraic relations among Goss’s zeta values on elliptic curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equidistribution of exponential sums indexed by a subgroup of fixed cardinality
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 65-94
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation