During the past century, the number monuments available for study from the Maya area has increased dramatically. The inscriptions on these monuments form the most detailed sources for the ancient history of the Maya. In many cases, the inscriptions contain Long Count, Tzolk'in, and Haab dates. Sometimes, a so-called Supplementary Series is embedded between the Tzolk'in and Haab dates; the Supplementary Series normally consists of the Lord of the Night glyph and the Lunar Series, which deals with the age of the moon and a six-lunar-month cycle. One dramatic example of a Long Count and Supplementary Series inscription comes from Coba, Stela 1 (Graham and von Euw Reference Graham and von Euw1997). This monument contains an unusual example of a Long Count with a very long introductory date consisting of 19 periods and using coefficients of 13. The date it refers to is clearly 13.0.0.0.0 4 Ahaw 8 K'umku, the base date of the current world age (Era count = 0). The units higher than Bak'tun are usually omitted, leaving a Long Count date with five periods (Figure 1).
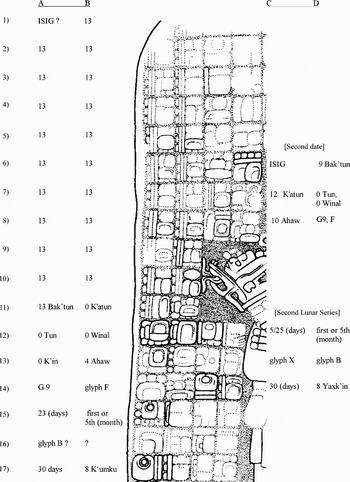
Figure 1. Coba, Stela 1 (A1–D17). Drawing: COB:St. 1 from Corpus of Maya Hieroglyphic Inscriptions, vol. 8, part 1:COBA, reproduced courtesy of the President and Fellows of Harvard College.
Coba, Stela 1 (A1–B17; Figure 1):
Long Count (A1–A13): 19 periods of 13 and 13.0.0.0.0
Tzolk'in (B13): 4 Ahaw
Lord of the Night (A14–B14): G9, Glyph F
Lunar Series (A15–A17): moon age = 23 days; first month; Glyph B and Glyph X (the name of the moon?); and (the length of the month was) 30 days.
Haab (B17): 8 Kumk'u
While for historical dates, one can assume that the age of the moon could have been observed, the moon ages for mythical dates can only be the result of backward calculation. The same is true for the lunar month count, since it can be compared with calendrical cycles to define larger units of time. The Maya used a system for counting lunar months that utilized six named months, but there was no common beginning month.
Mean phases of the moon repeat after one synodic month (29.530588 days). Today, the age of the moon is counted after the new moon, when the moon is near the sun and invisible. The moon age of the Maya Lunar Series, however, likely started at new light—that is, the first visibility of the waxing crescent one or two days after the new moon. Comparing the recorded moon age and the expected moon age calculated from the Long Count date results in deviations. Analysis of the Lunar Series shows that about 90% of the moon-age data fit together, give or take three days (Mickler Reference Mickler1982), although the accepted range of ±3 days (Teeple Reference Teeple1925a:545) is not very accurate. The possible reasons for this are rounding errors, a different definition of the starting point for counting the age of the moon (new moon or first or last visibility one to two days before or after the new moon), the influence of the local horizon and the latitude of the site, or seasonal effects. In the remaining 10% of the Lunar Series data, the moon-age error is greater than three days. I will test the hypothesis that some of the erroneous moon-age data resulted from backward calculations that used an incorrect length of the synodic month. The mythical dates from Palenque, Tikal, and Coba are the best inscriptions for checking a calculation method far back into the past.
Variations in the beginning month of the six-month lunar cycle produce another uncertainty. Teeple (Reference Teeple1930) proposed a period of a uniform count of the month (9.12.15.0.0–9.16.5.0.0) and periods before and after this time with variations in the regular six-month cycle. Detailed examination of this model finds it to be inaccurate. Instead, it can be shown that, for several sites, the beginning month in the lunar-month count changed after the accession of a new ruler and most likely depended on regional lunar-calendar styles.
LUNAR SERIES
The Structure of the Lunar Series
The Lunar Series is part of the Supplementary Series. It contains the age of the moon (a number and Glyph D and/or E); the count of months (a number and Glyph C); Glyphs X and B, whose meaning is uncertain; and the length of the month of 29 or 30 days (Teeple Reference Teeple1925b, Reference Teeple1930; Figure 2). The age of the moon is given as a number and/or a verb that describes the event when the month began (huliiy “since the arrival”) or ended (nak' “shut up,” “store” [Tzotzil], or “to end” [Yukatek]; Schele et al. Reference Schele, Grube and Fahsen1992:2–4). The number represented the number of days that had passed since the event. Values smaller than 20 were rendered mostly using bar-dot notation, and values greater than 20 were rendered as numerals between 1 and 9 and the sign for 20 (T683a: WINIK). However, it can be difficult to distinguish between the logogram for 20 and the logogram for HUL (part of huliiy) if the inscription is in a poor condition, which creates another possible source of confusion in reading the Lunar Series.
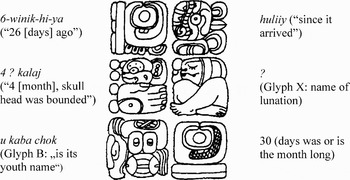
Figure 2. Lunar series from Palenque, Temple of the Sun Tablet. Drawing by the author, after Robertson Reference Robertson1991:4:95.
The coefficient of Glyph C, which is almost never greater than six, gives the current or last month in a six-month count (Teeple Reference Teeple1930; see Figure 3). Analysis of 321 C coefficients shows that about 48% of them fit a regular six-month count (Figure 6). Only on the Po Throne Panel, Bonampak, is the C coefficient greater than six, with an unusual Lunar Series given as 60 (days), 10 (days since) the arrival, the ninth month, 30 (days long) (Riese Reference Riese1988:50). The C coefficient is somehow related to Glyph X, as discussed by Erich Mickler (Reference Mickler1977:37–49). John Linden (Reference Linden1986) proposed an 18-month cycle to explain the C–X relationship, but his calculation confuses ancient moon-age formulas for calculating Glyphs C and X from Palenque and Copan with the modern formula for calculating moon ages.

Figure 3. The month count (Glyph C) with coefficient 1–6. Drawing by the author.
The Lunar Series Data Base
Collecting and comparing Lunar Series data published in E. Wyllys Andrews IV (Reference Andrews, Wyllys and Tax1951), Mickler (Reference Mickler1977, Reference Mickler1982), Linton Satterthwaite (Reference Satterthwaite and Tax1951), Linda Schele et al. (Reference Schele, Grube and Fahsen1992), and Teeple (Reference Teeple1930), with drawings and photographs, and an unpublished list (Bryan Wells, personal communication 1999) has resulted in a database of 361 Lunar Series. Not all of them are complete. Some examples are undated or have alternative readings of the Long Count date. In such cases, I have analyzed both variants. Because of the potential confusion in reading the logogram HUL/20, as noted earlier, the reading of the moon age can differ by 20 days from its expected value. I have not made corrections to the data to compensate for erosion and other factors. The analysis here is based on the uncorrected data.
In some cases, the published moon age and Long Count date seem to be based on an assumption that both should fit together and that the error in the moon age should be minimized. In this paper, I will not correct disagreements between expected and recorded lunar data. Instead, I will analyze them for possibly significant patterns (i.e., backward calculations). It is necessary to distinguish between small variations in the moon age and large errors caused by backward calculation. I will therefore discuss possible reasons for small variations in the moon age before testing the model of backward-calculated Lunar Series.
Variations in the Moon Age
Several factors can cause variations in the observed age of the moon. Influences on the first and last visibility of the moon are latitude, local horizon, azimuth of the setting or rising moon, and atmospheric conditions such as clouds, dust, and temperature, which affect refraction. To compare the given moon age against the expected moon age derived from modern formulas, one can use a correlation between the Maya and Christian calendars. However, it is also possible to calculate a mean moon age independent of such a correlation by using the mean synodic month of 29.530588 days. The maximum difference in results between the two methods is±.63 days, which shows the influence of several variations in the lunar orbit (Kelley and Milone Reference Kelley and Milone2005:30–35). Since the analyzed moon-age errors can be greater than ± 3 days, the influence of the Lunar Orbit anomaly and the other interfering variables is acceptable. It is necessary to use the correlation-independent analysis of the moon age because the correct correlation of the Maya and Christian calendars is still disputed (Fuls Reference Fuls2004, Reference Fuls2007; Kelley Reference Kelley, Leventhal and Kolata1983; Kelley and Milone Reference Kelley and Milone2005:359–360; Wells and Fuls Reference Wells and Fuls2000).
As indicated by the meaning of huliiy “since it arrived,” the moon-age count started at first visibility one or two days after the new moon. This phenomenon is called new light, and it is well known from ancient Babylonian observations up to the Islamic calendar as a starting point of a month (Kelley and Milone Reference Kelley and Milone2005:75). Conversely, the new moon or the last visibility one or two days before the new moon are also possible starting points of the Maya moon-age count. This would result in a variation of ±2 days in recorded moon ages. It is necessary for a correlation-independent analysis to determine a Long Count date falling on a known moon phase, such as the new moon. Because a solar eclipse must occur at new moon, I have used the Long Count dates in the eclipse table of the Dresden Codex. The mean new-moon date derived from this eclipse table is 1,412,848.4 days after the Era base date 13.0.0.0.0 4 Ahaw 8 Kumk'u.
Formula 1 determines the interval between a Long Count date (LC) and the mean new-moon date (LC0). It also calculates the remainder of the interval after subtracting multiples of the mean synodic month (U = 29.530588 days). Thus, the expected moon age (MA) is
Some of the Lunar Series data indicate a moon-age count starting at new moon, but we do not know how the Maya determined the date of the new moon if no eclipse was visible at the time. To calculate the mean lunar month as used by the Maya for backward calculations, the difference in the moon ages and the intervals are more important than the absolute error in each recorded moon age. For this reason, the starting point of the moon-age count is not critical to the discussion of the Palenque formula and other moon-age calculations. Only the backward calculation of the Lunar Series from Tikal, Temple 6, depends on the expected moon age, as discussed later.
The discussed variations in direct observation of the age of the moon has led to an acceptable error of ±3 days (Teeple Reference Teeple1930). Every error in the moon age that is greater than ±3 days will be considered a significant, albeit incorrect, lunar datum for further analysis. About 10% of the analyzed moon ages show variations greater than ±3 days.
The Hypothesis
I will test the hypothesis that many of the erroneous moon ages can be attributed to an error in calculation that resulted from using an incorrect length of the synodic lunar month. The magnitude of the error is a function of the interval between the dedication date and earlier events recorded on the monument. Classic-period Maya monuments normally record a series of events. In some cases, the date of the monument's dedication (verb tzakah) is recorded; in other cases, the dedication is assumed to be the chronologically latest date in the text. By the time the monument was carved and dedicated, the observational moon ages of earlier dates might have been unknown and, therefore, would have had to be calculated backward. The resulting estimates of moon ages thus would be only as accurate as the value of the synodic lunar month used in the calculation. The linear relationship between errors in the calculation of the moon age and the interval to the dedication date is evident in Figure 4.

Figure 4. Influence of an imprecise synodic-lunar-month value on backward calculated moon ages for earlier dates. Here, a synodic-lunar-month value of 29.5 is used instead of the actual 29.530588-day period.
THE CALCULATED MOON AGE AND MONTH COUNT
From which date was the Lunar Series calculated, and what value for the synodic lunar month was used? To test the hypothesis, I will assume that the Lunar Series of earlier dates were calculated backward from the date on which the monument was dedicated. If the calculation was performed not on that exact date but in the same year, the influence of the shift on the calculation's base date should be very small. The calculated moon age depends on the cumulative error from the date of dedication to the date referred to in the text. By alternating 29-day and 30-day months, the ancient Maya achieved a fractional value of 29.5 days for the mean length of the lunar month. If the Maya used a lunar month of 29.5 days instead of 29.530588 days, the error over the course of one year would be only .38 days. Thus, the dedication date is useful as an estimated base date for calculations. The small differences between the correct and calculated length of the lunar month (.030588 days in this example) accumulate over time and exceed the acceptable error of ±3 days after 7.9 years. For this reason, the interval between the Long Count date of the Lunar Series and the dedication date has to be greater than eight years to identify an error in calculation. Because the references to the Era base on the monuments must have been calculated backward, and because this interval is very long, these texts are useful in determining the length of the lunar month used by the Maya.
Review of the Palenque Formula
Teeple (Reference Teeple1930:65) proposed the Palenque formula using only three mythical dates and one historical date from the inscriptions on the Temple of the Cross group. The Palenque formula equates 2,392 days with 81 lunar months. Since the publication of Teeple's work, other inscriptions with mythical dates that include Lunar Series data have be found at Palenque (Stuart Reference Stuart2000). These new data have brought about a better understanding of the reading of the Lunar Series and necessitate a review of the Palenque formula. Further, improvements in data analysis have made statistical techniques available that were not used by Teeple (Reference Teeple1930). Linear-regression analysis, for example, gives a more precise measurement of the degree to which the data fit the model of the Palenque formula. There are a total of 10 complete Lunar Series statements from Palenque (Table 1). These data demonstrate that the Palenque formula, as proposed by Teeple (Reference Teeple1930), is used to calculate Lunar Series data backward for very early dates.
Table 1. Lunar Series data from Palenque

Notes: MA = moon age; C = lunar-month coeffcient; Head = head variant of Glyph C: young female (f), skull (s), or young male (y) (after Schele et al. Reference Schele, Grube and Fahsen1992); A = length of lunar month; B = Bak'tun; K' = K'atun; T = Tun; W = Winal; K = K'in; D = date.
asat: to lose or to die (Schele et al. Reference Schele, Grube and Fahsen1992:3).
Most of the moon ages count from “the birth” or “arrival” of the moon, starting with the first visibility of the moon. About 27 days later the Moon disappears (last visibility). This moon age of 27 days is described by two other Lunar Series, where the moon age glyph can be read as nak', which means “to end” (Table 1: Palace Tablet, date 1 and 12; Schele et al. Reference Schele, Grube and Fahsen1992:3). The historical moon-age data have a range of ±1 day. They fall 1.5 days after the new moon and confirm that the moon-age count started with the first visibility of the moon. The historical moon-age data form a strong base for the backward calculation of mythical dates and their Lunar Series. The moon-age error of the mythical dates depends on the distance to the dedication date of the monument, as shown in Figure 5.

Figure 5. The relationship between the distance to the dedication date and the moon-age error of the Lunar Series in Palenque (Table 2), using a 29.530864-day lunar month (Palenque formula).
The regression line in Figure 5 shows a significant linear relationship between error in the moon age and the interval of calculation (R = .993). This confirms the use of only one formula for the backward calculation and a value of 29.530846 days for the lunar month. This is the same month length used in the Palenque formula (29.530864), with a difference of only .000018 days, or one day in 4,492 years, thus confirming the Palenque formula. Using the Palenque formula, the moon age of mythical Long Count dates can be calculated using Formula 2:
In this formula, MALC is the moon age of the Long Count date; MADD is the moon age of the dedication date; I is the interval between the mythical date (LC) and the dedication date (DD); and P is the length of the month as used in the Palenque formula (2,392 days/81 months). If the moon age of the dedication date is not given, then it is possible to use Formula 1 to calculate the expected moon age of the dedication date. Table 2 compares the recorded moon ages and the backward calculation of the moon ages using the Palenque formula starting 1.5 days after the new moon. This comparison results in a mean error of ±.8 days between the calculated moon ages and those recorded on the monuments.
Table 2. Comparison of the recorded and calculated moon ages using the Palenque formula

Notes: DD = dedication date; MA = recorded moon age; MA-DD = calculated MA of DD after NL (Formula 1); NL = new light (one or two days after the new moon); MA-NL = calculated MA after NL using the Palenque formula; B = Bak'tun; K' = K'atun; T = Tun; W = Winal; K = K'in; D = date.
The Palenque formula works for the moon ages but not for the C coefficient of the Lunar Series. The C coefficients are sometimes off by −1, +1, or +2 months compared with a regular six-month count. The comparison of the C coefficients in Palenque shows no relationship with the eclipse cycle or with a lunar–solar counting system, which would have a relationship to the tropical year.4
Tikal
Although Tikal was a major political center during the Classic period, only a few Lunar Series are recorded on its monuments. On Temple 6, the end of Baktun 5 was recorded together with a Lunar Series. This was a backward calculation, since the earliest historical date for Tikal is 8.12.14.8.15 (Morley and Brainerd Reference Morley and Brainerd1983:104). I will assume that the dedication date was close to the time then the inscription was carved and therefore then the Lunar Series was calculated backward from it.
The glyphic facades of Temple 6 were dedicated by the twenty-eighth ruler of Tikal on 9.16.15.0.0 7 Ahaw 18 Pop (Martin and Grube Reference Martin and Grube2000:50). While this date does not have an associated Lunar Series, the data can be calculated using Formula 1. Conversely, the 5.0.0.0.0 12 Ahaw 3 Sak has a recorded moon age of 5 and a C coefficient of 5. These values do not match the expected Lunar Series values of 27.8 for the moon age and 4 for the C coefficient. The interval between these two dates is 696,600 days. A calculation using the modern astronomical value for the lunar month results in a value of 696,600 days =(3,931 × 6 + 3) × 29.530588 + 2.96 days, while the Palenque formula results in a value of 696,600 days = (3,931 × 6 + 2) × (29.532864) + 26 days. Using the Palenque formula leads to a backward-calculated moon age of 27.8 + 2.96−26 = 4.76 days (rounded to 5 days). The C coefficient would be 4 + 3 – 2 = 5. The differences between the recorded and expected values is explained by these calculations. Both parts of the Lunar Series for 5.0.0.0.0 fit the backward calculation using the Palenque formula and a regular six-month count.
Coba
On Coba, Stela 1, the Era base date and three other dates, including the Lunar Series, are recorded (see Table 3. The K'atun ending of date 2a, west, or date 2, east, are possible dedication dates. The mean length of 29.5 days per month would fit 9.12.10.5.12 as a calculation base date to backward calculate the Lunar Series data of the Era base date as follows: the interval between the Era base date and 9.12.10.5.12 is 1,386,112 days and equal to 7,831 × 6 × 29.5 + 25 days. The subtraction of 25 days from the moon age of the dedication date (MA = 19) results in 19–25 + 29.5 = 23.5 (rounded to 23 days). This is the moon age recorded on Stela 1 for the Era base date. The numbers of months are multiples of six, which means that the C coefficient does not change if a regular six-month count is used. The calculation fits the C coefficient of 1, as given for both dates.
Table 3. Lunar Series of Coba, Stela 1
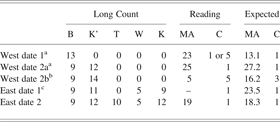
Note: B = Bak'tun; K' = K'atun; T = Tun; W = Winal; K = K'in; MA = moon age; C = C coefficient
aAfter Mickler Reference Mickler1982:63.
bAfter Schele et al. Reference Schele, Grube and Fahsen1992.
cMoon age eroded.
A check of the backward calculation from 9.12.10.5.12 to 9.12.0.0.0 10 Ahaw 8 Yaxk'in is less certain, since the interval is only 3,712 days, or about 10.2 years. The error in a backward calculation using 29.5 days as the length of the month would be 3.83 days. The backward calculated moon age of 9.12.0.0.0 should be 19–24.5 + 29.5 = 24 days (instead of 25 days). This is because the interval of 3,712 days is equal to 125 × 29.5 + 24.5 days. The C coefficient of both dates should be the same, since the interval is also a multiple of six months (21 × 6 × 29.5−5 days). The backward calculation fits the reading of the Long Count date, the moon age (with one day rounding error), and the C coefficient (after Mickler Reference Mickler1982:63). The alternative reading for this date by Schele et al. (Reference Schele, Grube and Fahsen1992) of 9.14.0.0.0 6 Ahaw 13 Muwan does not fit the expected moon age of the backward-calculated Era base date or the coefficient of the Tzolk'in (10) and Haab (8) dates (Figure 1).
VARIATIONS IN THE MONTH COUNT
The month count (Glyph C) with its coefficient is part of the Lunar Series and should be analyzed together with the moon age if the Lunar Series is the result of a calculation. The problem is that only 48% of the month coefficients fit a regular six-month count. The other 52% of the Lunar Series are off by one to three months (Figure 6). This means that one cannot use the month coefficient to reconstruct a Long Count date.

Figure 6. Deviation of the C coefficient (dC) compared with a regular six-month count.
Teeple (Reference Teeple1930) proposed a period with a regular six-month count between 9.12.15.0.0 and 9.16.5.0.0 (his Period of Uniformity). Satterthwaite (Reference Satterthwaite1959) shifted the boundaries of this Period of Uniformity on the basis of additional Lunar Series data (Mickler Reference Mickler1977:21–36), but a comparison of the C coefficient with a regular six-month count does not show a Period of Uniformity (Figure 6). The deviations in the C coefficient (dC) are distributed from the Early Classic to the Late Classic period. At El Zapote, all three of the recorded Lunar Series fit the expected value of C (dC = 0), while at Caracol, three (dC = 0) of five Lunar Series fit the regular six-month count (the two backward-calculated dates do not). The monuments of Altar de Sacrificios contain seven Lunar Series, and all of them, except the latest, are off by one month (dC = 1). At other sites, the C coefficient intermittently fits a regular six-month count (dC = 0; see Table 4). Additions to available Lunar Series data since Satterthwaite (Reference Satterthwaite1959) make it clear that the application of a regular six month count is both geographically and temporally irregular. A general Period of Uniformity does not exist.
Table 4. Deviation of the C coefficient for Classic-period rulers by site

Note: TYR = related to the tropical year.
aMartin and Grube Reference Martin and Grube2000.
At some sites (El Zapote and La Corona), small sample sizes make full analysis of variations in the Lunar Series difficult. Caracol, Dos Pilas, Naranjo, Quirigua, and Yaxchilan intermittently used the same regular six-month count, yet up to 36% of their Lunar Series still do not fit. The reason for these aberrant values requires further examination. The disagreements of the C coefficients from Caracol can be attributed to errors in backward calculation, as the moon age deviates by about 4.3 and 5.9 days from the expected values.
The Relationship between Month Count and Ruler
In the Lunar Series from Dos Pilas, La Corona, Naranjo, Piedras Negras, Yaxchilan, and Quirigua, a relationship can be seen between the C coefficient and the Ahaw who was ruling when the monument was erected (Table 4). This idea was first proposed by Heinrich Berlin-Neubart (Reference Berlin-Neubart1970:7, 10) for the royal genealogy of Piedras Negras and Quirigua.
The C coefficient for the five Lunar Series at Dos Pilas fits the uniform month count (dC = 0) until the last Lunar Series was erected by Ruler 3 on 9.15.4.6.11 (the C coefficient is off by −1). At Naranjo, there are three examples of Lunar Series on monuments erected by K'ahk' Ukalaw Chan Chaak (accession 9.16.4.10.18) and Itzamnaj K'awil (9.17.13.4.3–ca. 9.19.0.0.0), which fit the uniform month count; before the reign of these rulers, however, the C coefficients are irregular. At Quirigua, 12 of the C coefficients fit the uniform month count. One exception is an Old Era date, which was the result of a backward calculation that does not fit the system presented earlier. The C coefficients from the latest two monuments erected during the reign of K'ahk Tiliw Chan Yoaat (9.14.13.4.17–9.17.14.13.2) and K'ahk' Tiliw Chan Chaak (9.17.14.16.18– ca. 9.18.5.0.0) are off by one to three months. Why the latest two monuments erected by these rulers show a deviation in the C coefficient remains unexplained. At Yaxchilan, the C coefficients during the rule of Itzamnaj B'alam II (9.12.9.8.1–9.15.10.17.14) are irregular, but after 9.15.6.13.1 and during the reign of Yaxun B'alam IV (9.16.1.0.0–ca. 9.16.17.6.12), all C coefficients fit the uniform month count.
Four of five Lunar Series from La Corona fit the uniform month count (Table 4). They were erected between 9.14.9.9.14 and 9.18.15.0.0 by unknown rulers. Panel 1 is the only monument with a C coefficient that is off by one month. It was dedicated by Chakaw Nab Kan around 9.11.5.7.9. Since he died at 9.11.15.0.5, it is certain that he did not dedicate the later four monuments (Wells, personal communication 2002).
Piedras Negras
At Piedras Negras, the development of different month-count systems depended on the ruler who was responsible for erecting the monuments (Figure 7). The C coefficient of the first ruler does not fit the uniform system of six months. Instead, the starting dates of the month count for three Lunar Series of Yo'nal Ahk I (9.8.10.6.16–9.10.6.2.1) fall in the neighborhood of the same tropical-year station. This means that the sun was in the same position in relation to the spring equinox (Table 5). Subtracting the number of months and days as given by the C coefficient and the moon age from the associated Long Count date results in the starting date of the month count, as seen in Formulas 3–4:
In these formulas, LC(0,0) is the starting date of the month count; LC(MA,C) is the Long Count date of the Lunar Series; MA is the moon age; C is the C coefficient; and U is the length of the month. It is not known whether the C coefficient represents the number of elapsed months (Formula 3) or the current month position (Formula 4). For this reason, this analysis is relative; an absolute tropical-year position cannot be calculated.

Figure 7. Relationship of rulers in Piedras Negras and their lunar-month–counting system.
Table 5. Lunar Series data from Piedras Negras

Note: B = Bak'tun; K' = K'atun; T = Tun; W = Winal; K = K'in; MA = moon age; C = C coefficient; A = length of lunar month.
Berlin-Neubart (Reference Berlin-Neubart1970:6) read a C coefficient of 3 for Piedras Negras, Stela 25, but the third dot is most likely the ornamental element of the head variant and not part of numerical coefficient. The C coefficient of Stela 26 is 5 (Teeple Reference Teeple1930, based on Morley Reference Morley1937–1938:5.1:Plate 28 k). The interval between Stela 25 and Stela 26 approximates multiples of six months. This is why Berlin-Neubart (Reference Berlin-Neubart1970:5) proposed the same C coefficient for the two monuments. The assumption of a uniform six-month count that formed the basis of his proposal is untenable. The moon age of Stela 26 is off by five days compared with the moon age on Stela 25 (starting at new light; Morley Reference Morley1937–1938:5.1:Plate 28 k). If the intended moon age was eight instead of 13, the remainder would be 39.17 days and would fit within the range of the other remainders in relationship to the tropical year. The moon age on Stela 31 is eroded. To calculate an approximate starting date for the month count of Stela 31, the expected moon age of five, using the moon-age system of Stela 25, was inserted in Formula 3. The remainder of the tropical year for the starting date using a C coefficient of 3 would be about the same as for Stela 25 and Stela 26, even if the moon age is uncertain. The interval of the remainders to the tropical year is smaller than one month, which means that the month count during the reign of Ruler 1 of Piedras Negras started at the same moon age (probably the first visibility after the new moon), which falls at the same approximate tropical-year station. This kind of lunar–solar calendar was in common use in Greece (Seleschnikow Reference Seleschnikow1981:92–93).
There is no C coefficient higher than 6, which raises two questions. First, the tropical year (365.2422 days) is 10–11 days longer than 12 synodic lunar months. This difference would have required the insertion of an additional month about every three years to resynchronize the two periods. How the Maya might have accomplished this is unknown. Second, because the lunar-month count used six months, and the tropical year contains 12 synodic months, how did the Maya distinguish between the first series of six months and the second series of six months? Did the Maya check the position of the moon in comparison with a second tropical-year station, or did they just continue the count by restarting at month one? Unfortunately, there are not enough data to clarify the relationship of the month count to the tropical year.
Six monuments were erected by Ruler 2 of Piedras Negras (9.10.6.5.9–9.12.14.10.13). All of them are off by one month less than the uniform system (Berlin-Neubart Reference Berlin-Neubart1970:7). The next ruler, Yo'nal Ahk II (9.12.14.13.1–ca. 9.14.17.14.17), switched to the uniform system: nine of 10 Lunar Series on his monuments show the expected C coefficient (Figure 7). The only disagreement is on Stela 1, where Date A does not fit the moon age (by 14 days) or the C coefficient (+1 month). The Lunar Series of Date A was most likely a calculation error, because the Lunar Series of Date E on the same monument, 11,864 days later, fits the moon age and the uniform month system. The uniform system of the C coefficient was also preferred by two other rulers: Ruler 4 (9.14.18.3.13–9.16.6.11.17; five monuments) and Ha' K'in Xook (9.16.16.0.4–9.17.9.5.11; one monument). At 9.18.5.0.0, the month count may have switched back to the old system as established by Ruler 2, but there is only one monument erected by Ruler 7 (Stela 12), and this is not enough to demonstrate the shift.
Two monuments were erected by Yo'nal Ahk III (9.16.6.17.1–ca. 9.16.16.0.0; Table 5). The C coefficient on Stela 14 is uncertain. Teeple (Reference Teeple1930) gives 3, and Schele et al. (Reference Schele, Grube and Fahsen1992) give 4 as the C coefficient, although a drawing by John Montgomery (Mathews Reference Mathews1992:141) clearly shows only two dots (C = 2). If the C coefficient of Stela 14 is 2, then the remainder of the tropical year for both starting dates would be identical. A similar relationship of the month count to the tropical year was used by Ruler 1, but with a remainder that was 81–94 days less. This interval is about the same as the interval between the four tropical-year stations (89.2–93.5 days) or the interval between the first and second zenith passage at Piedras Negras (88 days). The absolute tropical-year position of the starting dates for the month count are uncertain for several reasons:
1 The C coefficient may give the number of elapsed months or the count of the current month (Formula 3 or 4).
2 The possible range is 30 days to reach the same moon phase every year as closely as possible to the same tropical-year station.
3 The issue of calendar correlation is still not settled, especially with regard to the tropical-year station (Fuls Reference Fuls2007; Kelley Reference Kelley, Leventhal and Kolata1983:179–184; Wells and Fuls Reference Wells and Fuls2000).
Again, these uncertainties make correlation-independent analysis necessary. The interval between 9.16.6.12.16 (Stela 14) and 9.16.14.14.18 (Stela 16) is 2,922 days, which is almost exactly equal to eight tropical years (+.062 days), as well as 99 synodic lunar months (−1.53 days; Table 5). The interval between 9.8.10.3.14 (Stela 25) and 9.9.14.10.0 (Stela 26) is 8,766 days, which is 3 × 2,922 days (Table 5). The intervals with multiples of eight tropical years support the relationship of the month count to the tropical year. The same cycle of 2,922 days was called Oktaetris and was proposed by the Greek Kleostatos as a lunar–solar calendar (Seleschnikow Reference Seleschnikow1981:93). I would suggest a similar idea for the month count at Piedras Negras during the reign of Yo'nal Ahk I and Yo'nal Ahk III.
CONCLUSIONS
Analysis of the Lunar Series shows that at least two different methods and formulas were used to calculate the moon's age and position in the six-month cycle. During the Classic period, there was no universal Period of Uniformity. The structure of the Lunar Series shows regional and temporal variations in the starting month of the six-month count and different approximations for the synodic month for calculating the age of the moon far into the past. The Palenque formula, confirmed by new Lunar Series data from Temple 18 and Temple 19 at Palenque, was also used at Tikal, but at Coba a less precise value of 29.5 days for the synodic month was employed. Satterthwaite (Reference Satterthwaite and Tax1951) discusses the seven-day range of moon-age errors and the possible reasons for it. Uncertainties in astronomical observations of the moon phase are likely a source of these errors, but it is now clear that imprecise backward calculations are an additional source of errors in moon ages. Lunar Series of mythical dates must be calculated backward and show large errors when compared with the actual age of the moon. Historical Lunar Series could also be the result of imprecise calculations, but calculation errors over short intervals are difficult to analyze. The errors in moon ages and month counts are unpredictable. For these reasons, it is hazardous to use lunar data to reconstruct a problematic calendric date.
Two different Lunar Series for the same date and from the same site are known from Pusilha and Naranjo. If the differences are not due to scribal errors, they may result from different calculation formulas or observations. Some of the Lunar Series data that have not been discussed in this paper should be the subject of further research. For example, Lunar Series data from Copan are irregular and may represent a different system.
Analysis of the month count shows a relationship between the month count and the ruler who dedicated the monument. The Lunar Series are part of the calendar calculations. The connection to changes in Maya rulers seems to suggest that rulers initiated new calculation methods on their accession. It is known from Classic Maya society that artists and scribes played an important role in the Classic-period royal courts. The capture of scribes, with fingers broken to prevent their service to their ruler, is recorded at Piedras Negras and Bonampak (Johnston Reference Johnston2001). A similar connection to the ruler can be assumed for other members of the court, who were responsible for astronomical and calendrical calculations, even if we have yet not found their titles or names in the corpus of Maya hieroglyphic inscriptions.
Resumen
Del periodo clásico de la cultura maya son conocidas alrededor de 321 inscripciones calendáricas sobre la edad de la luna, una cuenta lunar, la duración del mes, y otras informaciones referentes a la luna. En aproximación un 90% de todas las fechas la edad de la luna registrada concuerda con la edad esperada, sin embargo en los casos restantes persisten divergencias sin aclarar. Por razones arqueológicas e históricas está claro que las series lunares deben haber sido calculadas a partir de fechas mitológicas (siglos antes de la primera fecha histórica). Estas fechas son apropiadas para mostrar que la edad lunar fue calculada partiendo de la fecha de consagración o de la fecha de construcción del monumento, utilizando una determinada duración de mes. El análisis de nuevas series lunares de Palenque confirma la fórmula Palenque establecida por Teeple (Reference Teeple1930), que equipara 2,392 días con 81 meses. En este artículo se muestra por primera vez que la fórmula de Palenque también fue utilizada en Tikal hacia 9.16.15.0.0. En cambio, en Coba fue utilizada una duración de mes de 29.5 días para determinar la serie lunar de la fecha 13.0.0.0.0 4 Ajaw 8 K'umku en la Estela 1. En la segunda parte se rebate el “período de uniformidad” propuesto por Teeple (Reference Teeple1930) para una cuenta uniforme de seis meses en las series lunares. Se señala en cambio, la relación de la cuenta lunar con el gobernante de cada centro. La alteración en la cuenta lunar paralela a la subida al trono de un nuevo regente es demostrable para las series lunares de Dos Pilas, La Corona, Naranjo, Piedras Negras, Quirigua, y Yaxchilan. Esto permite deducir una estrecha relación entre los gobernantes y los expertos en calendarios versados en astronomía.
Acknowledgments
I am deeply indebted to David Stuart and Bryan Wells for their help in collecting Lunar Series data and their plain explanations of Maya hieroglyphs. I also thank David H. Kelley and Alexandre Tokovinine for their helpful comments.













