No CrossRef data available.
Article contents
ESTIMATES FOR APPROXIMATE SOLUTIONS TO A FUNCTIONAL DIFFERENTIAL EQUATION MODEL OF CELL DIVISION
Published online by Cambridge University Press: 12 March 2021
Abstract
The functional partial differential equation (FPDE) for cell division, 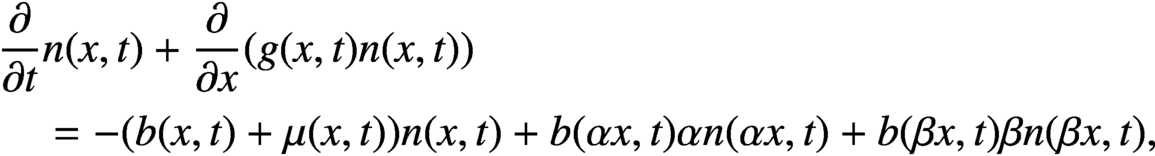
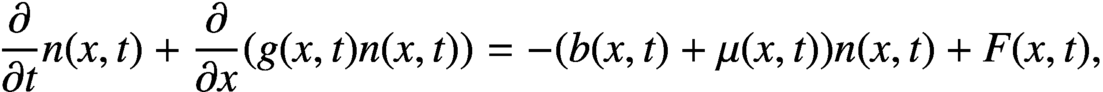
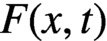 $F(x,t)$, can be solved by the method of characteristics. The difficulty is due to the advanced functional terms
$F(x,t)$, can be solved by the method of characteristics. The difficulty is due to the advanced functional terms 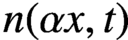 $n(\alpha x,t)$ and
$n(\alpha x,t)$ and 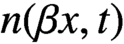 $n(\beta x,t)$, where
$n(\beta x,t)$, where 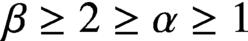 $\beta \ge 2 \ge \alpha \ge 1$, which arise because cells of size x are created when cells of size
$\beta \ge 2 \ge \alpha \ge 1$, which arise because cells of size x are created when cells of size 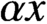 $\alpha x$ and
$\alpha x$ and 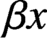 $\beta x$ divide.
$\beta x$ divide.
The nonnegative function, 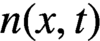 $n(x,t)$, denotes the density of cells at time t with respect to cell size x. The functions
$n(x,t)$, denotes the density of cells at time t with respect to cell size x. The functions 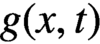 $g(x,t)$,
$g(x,t)$, 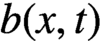 $b(x,t)$ and
$b(x,t)$ and 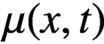 $\mu (x,t)$ are, respectively, the growth rate, splitting rate and death rate of cells of size x. The total number of cells,
$\mu (x,t)$ are, respectively, the growth rate, splitting rate and death rate of cells of size x. The total number of cells, 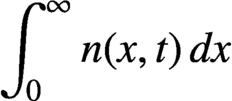 $\int _{0}^{\infty }n(x,t)\,dx$, coincides with the
$\int _{0}^{\infty }n(x,t)\,dx$, coincides with the 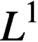 $L^1$ norm of n. The goal of this paper is to find estimates in
$L^1$ norm of n. The goal of this paper is to find estimates in 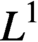 $L^1$ (and, with some restrictions,
$L^1$ (and, with some restrictions, 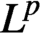 $L^p$ for
$L^p$ for 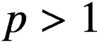 $p>1$) for a sequence of approximate solutions to the FPDE that are generated by solving the first-order PDE. Our goal is to provide a framework for the analysis and computation of such FPDEs, and we give examples of such computations at the end of the paper.
$p>1$) for a sequence of approximate solutions to the FPDE that are generated by solving the first-order PDE. Our goal is to provide a framework for the analysis and computation of such FPDEs, and we give examples of such computations at the end of the paper.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © Australian Mathematical Society 2021


