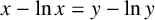1. Introduction
Consider the Lotka–Volterra system
 $$ \begin{align} \begin{aligned} &\frac{dS}{dt} = a S - b SX, \\ &\frac{dX}{dt} = c SX - d X, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{dS}{dt} = a S - b SX, \\ &\frac{dX}{dt} = c SX - d X, \end{aligned} \end{align} $$
where the nonnegative variable
![]() $S = S(t)$
represents prey and the nonnegative variable
$S = S(t)$
represents prey and the nonnegative variable
![]() $X = X(t)$
predator biomass, and a, b, c and d are positive constants. By introducing the nondimensional quantities
$X = X(t)$
predator biomass, and a, b, c and d are positive constants. By introducing the nondimensional quantities
system (1.1) takes the form
 $$ \begin{align} \begin{aligned} &\frac{ds}{d\tau} = (1-x)s, \\ &\frac{dx}{d\tau} = \alpha x (s-1), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{ds}{d\tau} = (1-x)s, \\ &\frac{dx}{d\tau} = \alpha x (s-1), \end{aligned} \end{align} $$
which, by the corresponding phase-plane equation, has its trajectories on level curves of
In this note, we derive analytical bounds for solutions of the Lotka–Volterra integral (1.3). Indeed, we prove that the solution
![]() $x < 1$
of the equation
$x < 1$
of the equation
satisfies the relation
![]() $x = z Y$
, where
$x = z Y$
, where
![]() $Y = y e^{-y}$
,
$Y = y e^{-y}$
,
![]() $1 < z < e$
and
$1 < z < e$
and
![]() $z = z(y)$
is a decreasing function of y. We also prove that the inequalities
$z = z(y)$
is a decreasing function of y. We also prove that the inequalities
![]() $1 < z_1 < z < z_2 < z_0 < e$
hold for z, where the
$1 < z_1 < z < z_2 < z_0 < e$
hold for z, where the
![]() $z_i$
terms are explicit functions of Y (see Theorem 2.1 in Section 2).
$z_i$
terms are explicit functions of Y (see Theorem 2.1 in Section 2).
To apply Theorem 2.1, consider a trajectory T of system (1.2) which passes through
![]() $(x_0, s_0)$
with
$(x_0, s_0)$
with
![]() $s_0> 1$
. If we aim for an estimate of the s-value for the next intersection of T with the line
$s_0> 1$
. If we aim for an estimate of the s-value for the next intersection of T with the line
![]() $x = x_0$
at, say
$x = x_0$
at, say
![]() $(x_0, s_1)$
, then we intend to estimate the solution of
$(x_0, s_1)$
, then we intend to estimate the solution of
![]() $V(x_0,s_0) = V(x_0,s_1)$
, where V is given by (1.3), that is, the solution
$V(x_0,s_0) = V(x_0,s_1)$
, where V is given by (1.3), that is, the solution
![]() $s_1 < 1 < s_0$
of
$s_1 < 1 < s_0$
of
According to the theorem, we find
in which the function z is decreasing and can be estimated so that
where
![]() $z_i = z_i(s_0)$
,
$z_i = z_i(s_0)$
,
![]() $i = 0,1,2$
. Likewise, if trajectory T passes through
$i = 0,1,2$
. Likewise, if trajectory T passes through
![]() $(x_0, s_0)$
with
$(x_0, s_0)$
with
![]() ${x_0> 1}$
, then we may find an estimate of the next intersection of T with the line
${x_0> 1}$
, then we may find an estimate of the next intersection of T with the line
![]() $s = s_0$
through the equation
$s = s_0$
through the equation
![]() $V(x_0,s_0) = V(x_1,s_0)$
, which boils down to
$V(x_0,s_0) = V(x_1,s_0)$
, which boils down to
![]() $x_1 - \ln x_1 = x_0 - \ln x_0$
. As above, we conclude, for the solution
$x_1 - \ln x_1 = x_0 - \ln x_0$
. As above, we conclude, for the solution
![]() $x_1 < 1 < x_0$
,
$x_1 < 1 < x_0$
,
where
![]() $z_i = z_i(x_0)$
,
$z_i = z_i(x_0)$
,
![]() $i = 0,1,2$
. Observe that any level of predator or prey can be chosen, giving estimates for the next intersection of the trajectory at the same predator or prey level. For example, if we wish to estimate the minimal predator biomass,
$i = 0,1,2$
. Observe that any level of predator or prey can be chosen, giving estimates for the next intersection of the trajectory at the same predator or prey level. For example, if we wish to estimate the minimal predator biomass,
![]() $x_{\min }$
, on a trajectory having maximal predator biomass
$x_{\min }$
, on a trajectory having maximal predator biomass
![]() $x_{\max }$
, then we use the fact that both maximal and minimal predator biomass are attained on the isocline
$x_{\max }$
, then we use the fact that both maximal and minimal predator biomass are attained on the isocline
![]() $x' = 0$
, that is, at the prey biomass
$x' = 0$
, that is, at the prey biomass
![]() $s_0 = 1$
. From (1.6), we obtain
$s_0 = 1$
. From (1.6), we obtain
where
![]() $z_i = z_i(x_{\max })$
,
$z_i = z_i(x_{\max })$
,
![]() $i = 0,1,2$
. Clearly, we can obtain the similar estimates for
$i = 0,1,2$
. Clearly, we can obtain the similar estimates for
![]() $s_{\min }$
as a function of
$s_{\min }$
as a function of
![]() $s_{\max }$
using (1.5) and
$s_{\max }$
using (1.5) and
![]() $x_0 = 1$
. Figure 1 shows the estimates for
$x_0 = 1$
. Figure 1 shows the estimates for
![]() $s_1$
in (1.5) with
$s_1$
in (1.5) with
![]() $(x_0,s_0) = (2,2)$
, and the estimates for
$(x_0,s_0) = (2,2)$
, and the estimates for
![]() $x_1$
in (1.6) with
$x_1$
in (1.6) with
![]() $(x_0,s_0) = (2,1/2)$
.
$(x_0,s_0) = (2,1/2)$
.

Figure 1 Trajectory T (solid blue curves) and the estimates of T marked with straight lines in black: estimates with
![]() $z_1$
and
$z_1$
and
![]() $z_2$
(solid),
$z_2$
(solid),
![]() $z_0$
(dashed), and
$z_0$
(dashed), and
![]() $1$
and e (dotted). The red dash-dotted lines mark the sought after intersection level. Estimates (a) for s in (1.5) with
$1$
and e (dotted). The red dash-dotted lines mark the sought after intersection level. Estimates (a) for s in (1.5) with
![]() $(x_0,s_0) = (2,2)$
, and (b) for x in (1.6) with
$(x_0,s_0) = (2,2)$
, and (b) for x in (1.6) with
![]() $(x_0,s_0) = (2,1/2)$
. Here,
$(x_0,s_0) = (2,1/2)$
. Here,
![]() $\alpha = 1$
.
$\alpha = 1$
.
In Theorem 2.2, we refine our arguments and derive more accurate bounds than those in Theorem 2.1 by introducing higher order Padé approximants in the constructions.
A literature survey shows extensive interest in Lotka–Volterra system (1.1) and its generalizations. To mention a few, we refer the reader to [Reference Clanet and Villermaux5, Reference Grozdanovski, Shepherd, Mercer and Roberts6, Reference Ito, Dieckmann and Metz9, Reference Murty and Rao16] and the references therein. Estimates valid for small prey biomass such as (1.5) may be of importance when studying the predators hunting strategies, for example, if there is a threshold of the prey level at which the predator chose to switch from their central prey and instead starts to feed on other sources. We give further motivations and demonstrations on how our theorems can be used to derive estimates of trajectories to more general dynamical systems in Section 3.
The solution of (1.4) can be written as
in which W denotes the principal branch of the Lambert W function. Therefore, our estimates in Theorems 2.1 and 2.2 imply bounds and approximations of this function, see Corollaries 2.3 and 2.4. In addition to population dynamics, the Lambert W function arises in many areas such as chemical and mechanical engineering, materials science, statistical mechanics, crystal growth, economy, viscous flows and flow through porous media (see for example, [Reference Åhag, Czyz and Lundow1–Reference Barry, Parlange, Li, Prommer, Cunningham and Stagnitti3, Reference Sharma, Shokeen, Saini, Sharma, Chetna, Kashyap, Guliani, Sharma, Khanna, Jain and Kapoor21] and references therein). In the next section, we present the main theorems and their proofs.
2. Statement and proofs of main results
We first prove the following analytical estimates.
Theorem 2.1. The solution
![]() $x<1$
of the equation
$x<1$
of the equation
![]() $x- \ln x = y - \ln y$
, where
$x- \ln x = y - \ln y$
, where
![]() $y>1$
, satisfies the relation
$y>1$
, satisfies the relation
![]() $x=z Y$
, where
$x=z Y$
, where
![]() $Y=ye^{-y}$
,
$Y=ye^{-y}$
,
![]() $1<z<e$
and
$1<z<e$
and
![]() $z = z(y)$
is decreasing in y. Moreover, the inequalities
$z = z(y)$
is decreasing in y. Moreover, the inequalities
![]() $1 < z_1 < z < z_2 < z_0 < e$
hold for z, where, for
$1 < z_1 < z < z_2 < z_0 < e$
hold for z, where, for
![]() $i = 1, 2$
,
$i = 1, 2$
,
 $$ \begin{align*} z_i &=\frac{1-d_i Y-\sqrt{(1-d_i Y)^2 - 4 c_i Y}}{2c_i Y}, \quad z_0 =\frac{1}{1-(e-1)Y},\notag\\ \quad d_i &= e-1-c_i e, \quad c_1=\frac{e-2}{e-1} \quad \text{and} \quad c_2=\frac{1}{e}. \end{align*} $$
$$ \begin{align*} z_i &=\frac{1-d_i Y-\sqrt{(1-d_i Y)^2 - 4 c_i Y}}{2c_i Y}, \quad z_0 =\frac{1}{1-(e-1)Y},\notag\\ \quad d_i &= e-1-c_i e, \quad c_1=\frac{e-2}{e-1} \quad \text{and} \quad c_2=\frac{1}{e}. \end{align*} $$
Proof. We begin by substituting
![]() $x=z Y$
into the equation of the theorem to obtain
$x=z Y$
into the equation of the theorem to obtain
and thus, since
![]() $Y = y e^{-y}$
,
$Y = y e^{-y}$
,
This equation has a unique solution for z, where
![]() $1<z<e$
, because
$1<z<e$
, because
![]() $0<Y<1/e$
for
$0<Y<1/e$
for
![]() $y>1$
,
$y>1$
,
![]() $Z(1)=0$
,
$Z(1)=0$
,
![]() $Z(e)=1/e$
and Z is increasing in z in the interval. Differentiation of (2.1) with respect to y,
$Z(e)=1/e$
and Z is increasing in z in the interval. Differentiation of (2.1) with respect to y,
 $$ \begin{align*}\frac{d}{dy}( y e^{-y}) = \frac{d}{dy}\bigg( \frac{\ln z(y)}{z(y)}\bigg),\end{align*} $$
$$ \begin{align*}\frac{d}{dy}( y e^{-y}) = \frac{d}{dy}\bigg( \frac{\ln z(y)}{z(y)}\bigg),\end{align*} $$
gives
Hence, z is decreasing in y.
To get the estimates for z, we intend to replace
![]() $\ln z$
in (2.1) by Padé approximations built on the rational functions
$\ln z$
in (2.1) by Padé approximations built on the rational functions
and then solve the remaining formulae for z. Immediately,
![]() $f_i(1) = 0$
and, by demanding
$f_i(1) = 0$
and, by demanding
![]() $f_i(e) = 1$
, we obtain
$f_i(e) = 1$
, we obtain
![]() $d_i = e - 1 - c_i e$
for
$d_i = e - 1 - c_i e$
for
![]() $i = 0, 1, 2$
. Taking
$i = 0, 1, 2$
. Taking
![]() $c_0 = 0$
makes
$c_0 = 0$
makes
![]() $f_0(z)$
a linear approximation and equating the derivatives of
$f_0(z)$
a linear approximation and equating the derivatives of
![]() $\ln z$
and
$\ln z$
and
![]() $f_2(z)$
at e gives
$f_2(z)$
at e gives
![]() $c_2 = 1/e$
. Similarly, equating the derivatives of
$c_2 = 1/e$
. Similarly, equating the derivatives of
![]() $\ln z$
and
$\ln z$
and
![]() $f_1(z)$
at
$f_1(z)$
at
![]() $1$
gives
$1$
gives
![]() $c_1 = (e-2)/(e-1)$
, and we prove below that these choices imply the central inequalities
$c_1 = (e-2)/(e-1)$
, and we prove below that these choices imply the central inequalities
Denote by
![]() $z^*$
the solution of (2.1). Then,
$z^*$
the solution of (2.1). Then,
![]() $Z(z)<Y$
for
$Z(z)<Y$
for
![]() $z<z^*$
and
$z<z^*$
and
![]() $Z(z)>Y$
for
$Z(z)>Y$
for
![]() $z>z^*$
. Thus, if
$z>z^*$
. Thus, if
![]() $Y={f_i(z_i)}/{z_i}<Z(z_i)$
, then
$Y={f_i(z_i)}/{z_i}<Z(z_i)$
, then
![]() $z^*<z_i$
, and if
$z^*<z_i$
, and if
![]() $Y={f_i(z_i)}/{z_i}>Z(z_i)$
, then
$Y={f_i(z_i)}/{z_i}>Z(z_i)$
, then
![]() $z^*>z_i$
. We now consider the functions
$z^*>z_i$
. We now consider the functions
![]() $g_i$
defined by
$g_i$
defined by
Calculating the derivative of
![]() $g_i(z)$
, gives
$g_i(z)$
, gives
We notice that
![]() $h_1(z)$
is negative between 1 and
$h_1(z)$
is negative between 1 and
![]() ${1}/{(e-2)^2}$
, positive between
${1}/{(e-2)^2}$
, positive between
![]() ${1}/{(e-2)^2}$
and e, and because
${1}/{(e-2)^2}$
and e, and because
![]() $g_1(1)=g_1(e)=0$
, we conclude that
$g_1(1)=g_1(e)=0$
, we conclude that
![]() $g_1(z)<0$
between 1 and e. Thus,
$g_1(z)<0$
between 1 and e. Thus,
![]() ${f_1(z)}/{z}>Z(z)$
, and because
${f_1(z)}/{z}>Z(z)$
, and because
![]() $z_1$
is the solution to
$z_1$
is the solution to
![]() ${f_1(z)}/{z}=Y$
, we get
${f_1(z)}/{z}=Y$
, we get
![]() $z^*>z_1$
.
$z^*>z_1$
.
Further,
![]() $h_2(z)$
is positive between 1 and
$h_2(z)$
is positive between 1 and
![]() $e\, (e-2)^2$
, negative between
$e\, (e-2)^2$
, negative between
![]() $e\, (e-2)^2$
and e, and because
$e\, (e-2)^2$
and e, and because
![]() $g_2(1)=g_2(e)=0$
, we conclude that
$g_2(1)=g_2(e)=0$
, we conclude that
![]() $g_2(z)>0$
between 1 and e. Thus,
$g_2(z)>0$
between 1 and e. Thus,
![]() ${f_2(z)}/{z}<Z(z)$
and because
${f_2(z)}/{z}<Z(z)$
and because
![]() $z_2$
is the solution to
$z_2$
is the solution to
![]() ${f_2(z)}/{z}=Y$
, we get
${f_2(z)}/{z}=Y$
, we get
![]() $z^*<z_2$
.
$z^*<z_2$
.
Furthermore,
![]() $h_0(z)$
is positive between 1 and
$h_0(z)$
is positive between 1 and
![]() $e-1$
, negative between
$e-1$
, negative between
![]() $e-1$
and e, and because
$e-1$
and e, and because
![]() $g_0(1)=g_0(e)=0$
, we conclude that
$g_0(1)=g_0(e)=0$
, we conclude that
![]() $g_0(z)>0$
between 1 and e. Thus,
$g_0(z)>0$
between 1 and e. Thus,
![]() ${f_0(z)}/{z}<Z(z)$
and because
${f_0(z)}/{z}<Z(z)$
and because
![]() $z_0$
is the solution to
$z_0$
is the solution to
![]() ${f_0(z)}/{z}=Y$
, we get
${f_0(z)}/{z}=Y$
, we get
![]() $z^*<z_0$
. We finish the proof by noting that a trivial calculation shows
$z^*<z_0$
. We finish the proof by noting that a trivial calculation shows
![]() $f_0(z) < f_2(z)$
for
$f_0(z) < f_2(z)$
for
![]() $1<z<e$
, implying
$1<z<e$
, implying
![]() $z_2 < z_0$
. This completes the proof.
$z_2 < z_0$
. This completes the proof.
A numerical solution of the equation
![]() $x -\ln x = y - \ln y$
together with the five bounds in Theorem 2.1, as well as the bounds in inequality (⋆) stated in Section 2.1, are plotted in Figure 2(a). Figure 2(b) shows the relative error.
$x -\ln x = y - \ln y$
together with the five bounds in Theorem 2.1, as well as the bounds in inequality (⋆) stated in Section 2.1, are plotted in Figure 2(a). Figure 2(b) shows the relative error.

Figure 2 (a) A numerical solution of the equation
![]() $x -\ln x = y - \ln y$
together with the five bounds in Theorem 2.1, as well as the bounds in display (⋆). (c) The Lambert W function together with the bounds in Corollary 2.3, the upper bound in display (⋆⋆) with
$x -\ln x = y - \ln y$
together with the five bounds in Theorem 2.1, as well as the bounds in display (⋆). (c) The Lambert W function together with the bounds in Corollary 2.3, the upper bound in display (⋆⋆) with
![]() $\bar {y} = X + 1$
and the series approximation in display (ser) with 2, 3, 4, 5 and 6 terms. (b,d) Relative error.
$\bar {y} = X + 1$
and the series approximation in display (ser) with 2, 3, 4, 5 and 6 terms. (b,d) Relative error.
While the estimates in Theorem 2.1 are not impressively accurate, we emphasize their simplicity and the fact that in biological systems, the Lotka–Volterra integral constitutes already an approximation of real systems, motivating us to strive for simple expressions rather than higher precision. We also remark that any equation of type
![]() $x - a \ln x = y - a \ln y$
,
$x - a \ln x = y - a \ln y$
,
![]() $0<x<a<y$
, can be transformed into the equation of Theorem 2.1 by scaling x and y.
$0<x<a<y$
, can be transformed into the equation of Theorem 2.1 by scaling x and y.
Using higher order Padé approximations in place of (2.2), we next build the following bounds.
Theorem 2.2. The inequalities
![]() $\tilde z_1 < z < \tilde z_i$
,
$\tilde z_1 < z < \tilde z_i$
,
![]() $i = 2,3$
, hold for z in Theorem
2.1
, where
$i = 2,3$
, hold for z in Theorem
2.1
, where
 $$ \begin{align*} \tilde z_i &=\frac{1 - 2a_i - d_i Y -\sqrt{(1-d_i Y)^2 - 4 Y(c_i - a_i(d_i + c_i))}}{2(c_i Y - a_i)} \end{align*} $$
$$ \begin{align*} \tilde z_i &=\frac{1 - 2a_i - d_i Y -\sqrt{(1-d_i Y)^2 - 4 Y(c_i - a_i(d_i + c_i))}}{2(c_i Y - a_i)} \end{align*} $$
in which
![]() $d_i = e-1-c_i\, e + a_i (e-1)^2$
,
$d_i = e-1-c_i\, e + a_i (e-1)^2$
,
![]() $i = 1, 2, 3,$
and where
$i = 1, 2, 3,$
and where
 $$ \begin{align*} a_1 = 1 - \frac{e}{(e-1)^2}, \quad a_2 &= \frac{3 - e}{2(e - 1)(e - 2)}, \quad a_3 = \frac{c_3\, e - 1}{e^2 - 1}, \notag\\ c_1 = e-1 -\frac{2}{e-1}, \quad c_2 &= \frac{e^2 - 4e + 5}{2(e - 1)(e - 2)}, \quad c_3 = \frac{2e - (e-1)^2}{2 + (e-1)^2}. \end{align*} $$
$$ \begin{align*} a_1 = 1 - \frac{e}{(e-1)^2}, \quad a_2 &= \frac{3 - e}{2(e - 1)(e - 2)}, \quad a_3 = \frac{c_3\, e - 1}{e^2 - 1}, \notag\\ c_1 = e-1 -\frac{2}{e-1}, \quad c_2 &= \frac{e^2 - 4e + 5}{2(e - 1)(e - 2)}, \quad c_3 = \frac{2e - (e-1)^2}{2 + (e-1)^2}. \end{align*} $$
Proof. The argument is very similar to the second part of the proof of Theorem 2.1. Instead of (2.2), we estimate
![]() $\ln z$
with the higher order Padé
$\ln z$
with the higher order Padé
 $$ \begin{align*}f_i(z)=\frac{z-1 + a_i(z-1)^2}{c_i z + d_i}, \quad i = 1, 2, 3, \quad 1 \leq z \leq e. \end{align*} $$
$$ \begin{align*}f_i(z)=\frac{z-1 + a_i(z-1)^2}{c_i z + d_i}, \quad i = 1, 2, 3, \quad 1 \leq z \leq e. \end{align*} $$
Solving the remaining expression of (2.1), which is only a second-order equation, gives the desired expression for z, and equating
![]() $\ln z$
with
$\ln z$
with
![]() $f_i(z)$
at e immediately gives
$f_i(z)$
at e immediately gives
![]() ${d_i = e - 1 - c_i e + a_i (e - 1)^2.}$
We will show
${d_i = e - 1 - c_i e + a_i (e - 1)^2.}$
We will show
by observing that the derivative of
![]() $g_i(z)=\ln z -f_i(z)$
yields
$g_i(z)=\ln z -f_i(z)$
yields
in which
Equating the first derivatives of
![]() $\ln z$
and
$\ln z$
and
![]() $f_1(z)$
at endpoints 1 and e gives
$f_1(z)$
at endpoints 1 and e gives
![]() $a_1$
and
$a_1$
and
![]() $c_1$
building the lower bound
$c_1$
building the lower bound
![]() $\tilde z_1$
. We notice that
$\tilde z_1$
. We notice that
![]() $h_1(z)$
has three real roots, 1,
$h_1(z)$
has three real roots, 1,
![]() $z_r \approx 1.66$
and e, is negative between 1 and
$z_r \approx 1.66$
and e, is negative between 1 and
![]() $z_r$
, positive between
$z_r$
, positive between
![]() $z_r$
and e, and because
$z_r$
and e, and because
![]() $g_1(1) = g_1(e) = 0,$
we conclude that
$g_1(1) = g_1(e) = 0,$
we conclude that
![]() $g_1(z) < 0$
between 1 and e. Thus,
$g_1(z) < 0$
between 1 and e. Thus,
![]() ${f_1(z)}/{z}>Z(z)$
, and because
${f_1(z)}/{z}>Z(z)$
, and because
![]() $\tilde z_1$
is the solution of
$\tilde z_1$
is the solution of
![]() ${f_1(z)}/{z}=Y$
, we get
${f_1(z)}/{z}=Y$
, we get
![]() $z^*>\tilde z_1$
.
$z^*>\tilde z_1$
.
Equating first and second derivatives of
![]() $\ln z$
and
$\ln z$
and
![]() $f_2(z)$
at
$f_2(z)$
at
![]() $z = 1$
gives
$z = 1$
gives
![]() $a_2$
and
$a_2$
and
![]() $c_2$
building the upper bound
$c_2$
building the upper bound
![]() $\tilde z_2$
. We notice that
$\tilde z_2$
. We notice that
![]() $h_2(z)$
has three real roots, 1, 1,
$h_2(z)$
has three real roots, 1, 1,
![]() $z_r \approx 2.12$
, is positive between 1 and
$z_r \approx 2.12$
, is positive between 1 and
![]() $z_r$
, negative between
$z_r$
, negative between
![]() $z_r$
and e, and because
$z_r$
and e, and because
![]() $g_2(1)=g_2(e)=0$
, we conclude that
$g_2(1)=g_2(e)=0$
, we conclude that
![]() $g_2(z)>0$
between 1 and e. Thus,
$g_2(z)>0$
between 1 and e. Thus,
![]() ${f_2(z)}/{z}<Z(z)$
and because
${f_2(z)}/{z}<Z(z)$
and because
![]() $\tilde z_2$
is the solution of
$\tilde z_2$
is the solution of
![]() ${f_2(z)}/{z}=Y$
, we get
${f_2(z)}/{z}=Y$
, we get
![]() $z^*<\tilde z_2$
.
$z^*<\tilde z_2$
.
Equating first and second derivatives of
![]() $\ln z$
and
$\ln z$
and
![]() $f_3(z)$
at
$f_3(z)$
at
![]() $z = e$
gives
$z = e$
gives
![]() $a_3$
and
$a_3$
and
![]() $c_3$
building the upper bound
$c_3$
building the upper bound
![]() $\tilde z_3$
. We notice that
$\tilde z_3$
. We notice that
![]() $h_3(z)$
has three real roots,
$h_3(z)$
has three real roots,
![]() $z_r\approx 1.296,e,e$
, is positive between 1 and
$z_r\approx 1.296,e,e$
, is positive between 1 and
![]() $z_r$
, negative between
$z_r$
, negative between
![]() $z_r$
and e, and because
$z_r$
and e, and because
![]() $g_3(1)=g_3(e)=0$
, we conclude that
$g_3(1)=g_3(e)=0$
, we conclude that
![]() $g_3(z)>0$
between 1 and e. Thus,
$g_3(z)>0$
between 1 and e. Thus,
![]() ${f_3(z)}/{z}<Z(z)$
and because
${f_3(z)}/{z}<Z(z)$
and because
![]() $z_3$
is the solution of
$z_3$
is the solution of
![]() ${f_3(z)}/{z}=Y$
, we get
${f_3(z)}/{z}=Y$
, we get
![]() $z^*<\tilde z_3$
; this completes the proof.
$z^*<\tilde z_3$
; this completes the proof.
Of the two upper bounds, they match better near the side where the derivatives are equated, naturally. Figure 3(a) shows the relative error of the bounds in Theorem 2.2, the sharpest bounds from Theorem 2.1 and those given in (⋆).

Figure 3 (a) Relative error of the bounds in Theorem 2.2, the sharpest bounds from Theorem 2.1 and those given in display (⋆). (b) Relative error of the bounds on the Lambert W function in Corollary 2.4, the sharpest bounds from Corollary 2.3, the bound in display (⋆⋆) with
![]() $\bar {y} = X + 1$
, and the series approximation in display (ser) with 2, 3, 4, 5 and 6 terms. In the legend,
$\bar {y} = X + 1$
, and the series approximation in display (ser) with 2, 3, 4, 5 and 6 terms. In the legend,
![]() $\text {tz}_i = \tilde z_i$
and
$\text {tz}_i = \tilde z_i$
and
![]() $\text {TZ}_i = \widetilde {\mathcal {Z}_i}$
.
$\text {TZ}_i = \widetilde {\mathcal {Z}_i}$
.
2.1. Implications for the Lambert W function
For real numbers X and u, the equation
can be solved for u only if
![]() $X \geq -1/e$
; gets
$X \geq -1/e$
; gets
![]() $u = W(X)$
if
$u = W(X)$
if
![]() $X \geq 0$
and the two values
$X \geq 0$
and the two values
![]() ${u = W(X)}$
and
${u = W(X)}$
and
![]() $u = W_{-1}(X)$
if
$u = W_{-1}(X)$
if
![]() $-1/e \leq X < 0$
. Here, W is the upper (principal) branch and
$-1/e \leq X < 0$
. Here, W is the upper (principal) branch and
![]() $W_{-1}$
the lower branch of the Lambert W function, (see Figure 4).
$W_{-1}$
the lower branch of the Lambert W function, (see Figure 4).

Figure 4 The Lambert W function.
The equation
![]() $x-\ln {x} = y - \ln {y}$
,
$x-\ln {x} = y - \ln {y}$
,
![]() $x \in (0,1)$
,
$x \in (0,1)$
,
![]() $y\in (1,\infty )$
can be written as
$y\in (1,\infty )$
can be written as
and thus
![]() $x = -W(-ye^{-y}) = -W(-Y)$
. However, following the notation in Theorem 2.1, we also have
$x = -W(-ye^{-y}) = -W(-Y)$
. However, following the notation in Theorem 2.1, we also have
and hence Theorem 2.1 gives estimates of the function
![]() $-W(-ye^{-y})$
. In our case,
$-W(-ye^{-y})$
. In our case,
![]() $-Y \in (-e^{-1},0)$
,
$-Y \in (-e^{-1},0)$
,
![]() $x \in (0,1)$
and hence, we are in the upper (principal) branch. We remark that the function
$x \in (0,1)$
and hence, we are in the upper (principal) branch. We remark that the function
![]() $W(-ye^{-y})$
appears also in the classic problem of a projectile moving through a linearly resisting medium [Reference Morales15, Reference Packel and Yuen20, Reference Stewart23, Reference Warburton and Wang25], and that several bounds for
$W(-ye^{-y})$
appears also in the classic problem of a projectile moving through a linearly resisting medium [Reference Morales15, Reference Packel and Yuen20, Reference Stewart23, Reference Warburton and Wang25], and that several bounds for
![]() $W(-ye^{-y})$
were derived in [Reference Stewart24]. For example, [Reference Stewart24, Theorems 3.5 and 3.7] imply
$W(-ye^{-y})$
were derived in [Reference Stewart24]. For example, [Reference Stewart24, Theorems 3.5 and 3.7] imply
whenever
![]() $y> 1$
. (In [Reference Stewart24], the right-hand side is
$y> 1$
. (In [Reference Stewart24], the right-hand side is
![]() $2\ln {y} - 1$
, but their proof holds for (⋆) as well.) Figure 2(a,b) shows the function
$2\ln {y} - 1$
, but their proof holds for (⋆) as well.) Figure 2(a,b) shows the function
![]() $x = - W(-ye^{-y})$
together with our estimates and the estimates in (⋆).
$x = - W(-ye^{-y})$
together with our estimates and the estimates in (⋆).
Next, let
![]() $X = -Y$
and observe that
$X = -Y$
and observe that
Noticing also that
![]() $z = z(y)$
depends only on
$z = z(y)$
depends only on
![]() $Y = -X$
, the estimates in Theorem 2.1 imply the following approximations of the Lambert W function.
$Y = -X$
, the estimates in Theorem 2.1 imply the following approximations of the Lambert W function.
Corollary 2.3. Let
![]() $W(X)$
be the principal branch of the Lambert W function. Then,
$W(X)$
be the principal branch of the Lambert W function. Then,
whenever
![]() $-1/e \leq X \leq 0$
, where for
$-1/e \leq X \leq 0$
, where for
![]() $i=1,2$
,
$i=1,2$
,
 $$ \begin{align*} \mathcal Z_i(X) &=\frac{-1-d_i X+\sqrt{(1+d_i X)^2 + 4 c_i X}}{2c_i}, \quad \mathcal Z_0(X) = \frac{X}{1+(e-1)X},\\ \quad d_i &= e-1-c_i e, \quad c_1=\frac{e-2}{e-1} \quad \text{and} \quad c_2=\frac{1}{e}. \end{align*} $$
$$ \begin{align*} \mathcal Z_i(X) &=\frac{-1-d_i X+\sqrt{(1+d_i X)^2 + 4 c_i X}}{2c_i}, \quad \mathcal Z_0(X) = \frac{X}{1+(e-1)X},\\ \quad d_i &= e-1-c_i e, \quad c_1=\frac{e-2}{e-1} \quad \text{and} \quad c_2=\frac{1}{e}. \end{align*} $$
While the estimates in Corollary 2.3 are not impressively accurate, we emphasize their simplicity and that we will derive more accurate bounds for the Lambert W function in Corollary 2.4 below. We proceed by comparing the bounds in Corollary 2.3 with other simple estimates, for example, the following upper bound given in [Reference Hoorfar and Hassani7]:
valid for
![]() $X \geq - 1 / e$
, where
$X \geq - 1 / e$
, where
![]() $\bar {y}> 1 / e$
is a degree of freedom. Moreover, the Taylor series of W around 0 yields
$\bar {y}> 1 / e$
is a degree of freedom. Moreover, the Taylor series of W around 0 yields
 $$ \begin{align} W(X) = \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!} X^n = X - X^2 + \frac{3}{2} X^3 - \frac{8}{3} X^4 + \frac{125}{24} X^5 - \cdots, \end{align} $$
$$ \begin{align} W(X) = \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!} X^n = X - X^2 + \frac{3}{2} X^3 - \frac{8}{3} X^4 + \frac{125}{24} X^5 - \cdots, \end{align} $$
and an approximation with relative error less than
![]() $0.013\%$
can be found in [Reference Barry, Parlange, Li, Prommer, Cunningham and Stagnitti3, (7), (8) and (9)], to which we also refer the reader for an extensive list of applications for the Lambert W function. Figure 2(c,d) shows the Lambert W function together with our estimates in Corollary 2.3, the upper bound (⋆⋆) with
$0.013\%$
can be found in [Reference Barry, Parlange, Li, Prommer, Cunningham and Stagnitti3, (7), (8) and (9)], to which we also refer the reader for an extensive list of applications for the Lambert W function. Figure 2(c,d) shows the Lambert W function together with our estimates in Corollary 2.3, the upper bound (⋆⋆) with
![]() $\bar {y} = X + 1$
, the series approximation (ser) with 2, 3, 4, 5 and 6 terms in panel (c), as well as the relative error in panel (d).
$\bar {y} = X + 1$
, the series approximation (ser) with 2, 3, 4, 5 and 6 terms in panel (c), as well as the relative error in panel (d).
In the same way as Theorem 2.1 yields Corollary 2.3, the higher order Padé approximations in Theorem 2.2 imply the following bounds of the Lambert W function.
Corollary 2.4. Let
![]() $W(X)$
be the principal branch of the Lambert W function. Then,
$W(X)$
be the principal branch of the Lambert W function. Then,
whenever
![]() $-1/e \leq X \leq 0$
, where for
$-1/e \leq X \leq 0$
, where for
![]() $i = 1,2,3,$
$i = 1,2,3,$
 $$ \begin{align*} \widetilde{\mathcal Z_i}(X) &=\frac{2a_i -1-d_i X+\sqrt{(1+d_i X)^2 + 4 X(c_i - a_i(d_i + c_i))}}{2(c_i + a_i X^{-1})} \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal Z_i}(X) &=\frac{2a_i -1-d_i X+\sqrt{(1+d_i X)^2 + 4 X(c_i - a_i(d_i + c_i))}}{2(c_i + a_i X^{-1})} \end{align*} $$
and where the coefficients
![]() $a_i, c_i$
and
$a_i, c_i$
and
![]() $d_i$
are as in Theorem
2.2
.
$d_i$
are as in Theorem
2.2
.
Figure 3(b) shows the relative error of the bounds on the Lambert W function in Corollary 2.4, the sharpest bounds from Corollary 2.3, the bound in (⋆⋆) with
![]() ${\bar {y} = X + 1}$
, and the series approximation (ser) with 2, 3, 4, 5 and 6 terms.
${\bar {y} = X + 1}$
, and the series approximation (ser) with 2, 3, 4, 5 and 6 terms.
3. Applications to more general predator–prey systems
Consider a general predator–prey system on the form
 $$ \begin{align} \begin{aligned} \frac{dS}{dt} &= H(S) - q \varphi(S) X, \\ \frac{dX}{dt} &= p \varphi(S) X - d X, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{dS}{dt} &= H(S) - q \varphi(S) X, \\ \frac{dX}{dt} &= p \varphi(S) X - d X, \end{aligned} \end{align} $$
where the nonnegative variable
![]() $S = S(t)$
represents the prey biomass, the nonnegative variable
$S = S(t)$
represents the prey biomass, the nonnegative variable
![]() $X = X(t)$
represents the predator biomass,
$X = X(t)$
represents the predator biomass,
![]() $\varphi $
is nondecreasing,
$\varphi $
is nondecreasing,
![]() ${\varphi (0) = H(0) = 0}$
, and parameters
${\varphi (0) = H(0) = 0}$
, and parameters
![]() $p, q, d$
are positive. Systems of type (3.1) have been extensively studied through the last centuries, see for example, [Reference Cheng4, Reference Hsu and Shi8, Reference Lindström10, Reference Lindström11, Reference Lundström and Söderbacka13, Reference Lundström and Söderbacka14] and the references therein.
$p, q, d$
are positive. Systems of type (3.1) have been extensively studied through the last centuries, see for example, [Reference Cheng4, Reference Hsu and Shi8, Reference Lindström10, Reference Lindström11, Reference Lundström and Söderbacka13, Reference Lundström and Söderbacka14] and the references therein.
Often, functions H and
![]() $\varphi $
are defined by
$\varphi $
are defined by
where, most commonly,
![]() $n = 1$
or
$n = 1$
or
![]() $n = 2$
. In the case of (3.2), system (3.1) is usually referred to as a Rosenzweig–MacArthur predator–prey system. If
$n = 2$
. In the case of (3.2), system (3.1) is usually referred to as a Rosenzweig–MacArthur predator–prey system. If
then system (3.1) boils down to the Lotka–Volterra equations (1.2).
We now intend to analyse the general system (3.1) using our estimates in Theorem 2.1. Without loss of generality, assume that
![]() $q = 1$
. The phase-plane equation yields
$q = 1$
. The phase-plane equation yields
where
![]() $F(S) = H(S) / \varphi (S)$
. Let us replace
$F(S) = H(S) / \varphi (S)$
. Let us replace
![]() $F(S)$
by a constant
$F(S)$
by a constant
![]() $\overline F$
for the moment, and observe that then integrating gives
$\overline F$
for the moment, and observe that then integrating gives
 $$ \begin{align*} \int\bigg(p - \frac{d}{\varphi(S)}\bigg)\,dS = \int\bigg(\frac{{\overline F}}{X} - 1\bigg)\, dX, \end{align*} $$
$$ \begin{align*} \int\bigg(p - \frac{d}{\varphi(S)}\bigg)\,dS = \int\bigg(\frac{{\overline F}}{X} - 1\bigg)\, dX, \end{align*} $$
and thus the system can, under reasonable assumptions on
![]() $\varphi $
and H, be analysed by the generalized Lotka–Volterra integral
$\varphi $
and H, be analysed by the generalized Lotka–Volterra integral
 $$ \begin{align*} V_{\overline F}(X,S) = pS - d\int\frac{dS}{\varphi(S)} + X - {\overline F} \ln{X}. \end{align*} $$
$$ \begin{align*} V_{\overline F}(X,S) = pS - d\int\frac{dS}{\varphi(S)} + X - {\overline F} \ln{X}. \end{align*} $$
Moreover,
 $$ \begin{align} \nabla V_{\overline F} = \bigg(1 - \frac{\overline F}{X} , p - \frac{d}{\varphi(S)}\bigg), \end{align} $$
$$ \begin{align} \nabla V_{\overline F} = \bigg(1 - \frac{\overline F}{X} , p - \frac{d}{\varphi(S)}\bigg), \end{align} $$
and
 $$ \begin{align} \frac{d V_{\overline F}}{d t} &= \bigg(p - \frac{d}{\varphi(S)}\bigg) \frac{dS}{dt} + \bigg(1 - \frac{\overline F}{X} \bigg) \frac{dX}{dt} = (p\varphi(S) - d) (F(S) - {\overline F} ). \end{align} $$
$$ \begin{align} \frac{d V_{\overline F}}{d t} &= \bigg(p - \frac{d}{\varphi(S)}\bigg) \frac{dS}{dt} + \bigg(1 - \frac{\overline F}{X} \bigg) \frac{dX}{dt} = (p\varphi(S) - d) (F(S) - {\overline F} ). \end{align} $$

Figure 5 Geometry in the construction of estimates.
To proceed, we consider a trajectory T of system (3.1) with initial condition
![]() $(X_0,S_0)$
, where
$(X_0,S_0)$
, where
![]() $X_0> F(S_0)$
and
$X_0> F(S_0)$
and
![]() $S_0$
satisfies
$S_0$
satisfies
![]() $\varphi (S_0) < d/p$
. Observe that
$\varphi (S_0) < d/p$
. Observe that
![]() $X = F(S)$
and
$X = F(S)$
and
![]() $\varphi (S) = d/p$
give isoclines and that both S and X are decreasing initially. Suppose that until T intersects
$\varphi (S) = d/p$
give isoclines and that both S and X are decreasing initially. Suppose that until T intersects
![]() $S = S_0$
the next time, T stays in a part of the state space where there exist positive
$S = S_0$
the next time, T stays in a part of the state space where there exist positive
![]() $\underline {F}$
and
$\underline {F}$
and
![]() $\overline {F}$
such that
$\overline {F}$
such that
It then follows from (3.3) and (3.4) that trajectory T starting at
![]() $(X_0,S_0)$
remains trapped between the curves
$(X_0,S_0)$
remains trapped between the curves
![]() $\underline {S}$
and
$\underline {S}$
and
![]() $\overline {S}$
, defined through
$\overline {S}$
, defined through
(see Figure 5). Moreover, the “barriers”
![]() $\underline {S}$
and
$\underline {S}$
and
![]() $\overline {S}$
are convex with minimum at
$\overline {S}$
are convex with minimum at
![]() $X = \underline {F}$
and
$X = \underline {F}$
and
![]() $X = \overline {F}$
, and intersect
$X = \overline {F}$
, and intersect
![]() $S = S_0$
a second time at
$S = S_0$
a second time at
![]() $X = \underline {X}_1$
and
$X = \underline {X}_1$
and
![]() $X = \overline {X}_1$
, respectively. For the next intersection of T with
$X = \overline {X}_1$
, respectively. For the next intersection of T with
![]() $S = S_0$
at
$S = S_0$
at
![]() $(X_1,S_0)$
, it necessarily holds that
$(X_1,S_0)$
, it necessarily holds that
where
and
By setting
![]() $x = {\underline X_1}/{\underline {F}}$
and
$x = {\underline X_1}/{\underline {F}}$
and
![]() $y = {X_0}/{\underline {F}}$
, the first equation reads
$y = {X_0}/{\underline {F}}$
, the first equation reads
and since
![]() $y = {X_0}/{\underline {F}}> 1$
, an application of Theorem 2.1 gives
$y = {X_0}/{\underline {F}}> 1$
, an application of Theorem 2.1 gives
where z is a decreasing function of y. As the same argument applies to the upper barrier, we conclude
 $$ \begin{align*} z\bigg(\frac{X_0}{\underline{F}}\bigg){X_0} e^{-{X_0}/{\underline{F}}} = \underline X_1 < X_1 < \overline X_1 = z\bigg(\frac{X_0}{\overline{F}}\bigg){X_0} e^{-{X_0}/{\overline{F}}}. \end{align*} $$
$$ \begin{align*} z\bigg(\frac{X_0}{\underline{F}}\bigg){X_0} e^{-{X_0}/{\underline{F}}} = \underline X_1 < X_1 < \overline X_1 = z\bigg(\frac{X_0}{\overline{F}}\bigg){X_0} e^{-{X_0}/{\overline{F}}}. \end{align*} $$
Moreover, since
where W is the principal branch of the Lambert W function, we also have
 $$ \begin{align*} -\underline{F} W\bigg(-\frac{X_0}{\underline{F}}e^{-{X_0}/{\underline{F}}} \bigg) = \underline X_1 < X_1 < \overline X_1 = -\overline{F} W\bigg(\frac{X_0}{\overline{F}} e^{-{X_0}/{\overline{F}}}\bigg). \end{align*} $$
$$ \begin{align*} -\underline{F} W\bigg(-\frac{X_0}{\underline{F}}e^{-{X_0}/{\underline{F}}} \bigg) = \underline X_1 < X_1 < \overline X_1 = -\overline{F} W\bigg(\frac{X_0}{\overline{F}} e^{-{X_0}/{\overline{F}}}\bigg). \end{align*} $$
Finally, summarizing and applying Theorem 2.1 for estimating z yields the following result.
Theorem 3.1. Suppose that T is a trajectory of system (3.1) with initial condition
![]() $(X_0,S_0)$
satisfying
$(X_0,S_0)$
satisfying
![]() $X_0> F(S_0)$
and
$X_0> F(S_0)$
and
![]() $\varphi (S_0) < d/p$
. Suppose also that, until T intersects
$\varphi (S_0) < d/p$
. Suppose also that, until T intersects
![]() $S = S_0$
the next time, T stays in a part of the state space where (3.5) is satisfied. Then, for the next intersection of trajectory T with
$S = S_0$
the next time, T stays in a part of the state space where (3.5) is satisfied. Then, for the next intersection of trajectory T with
![]() $S = S_0$
at
$S = S_0$
at
![]() $(X_1,S_0)$
, it holds that
$(X_1,S_0)$
, it holds that
 $$ \begin{align*} -\underline{F} W\bigg(-\frac{X_0}{\underline{F}}e^{-{X_0}/{\underline{F}}} \bigg) < X_1 < -\overline{F} W\bigg(\frac{X_0}{\overline{F}} e^{-{X_0}/{\overline{F}}}\bigg) \end{align*} $$
$$ \begin{align*} -\underline{F} W\bigg(-\frac{X_0}{\underline{F}}e^{-{X_0}/{\underline{F}}} \bigg) < X_1 < -\overline{F} W\bigg(\frac{X_0}{\overline{F}} e^{-{X_0}/{\overline{F}}}\bigg) \end{align*} $$
and
where
![]() $z_1 = z_1({X_0}/{\underline {F}})$
,
$z_1 = z_1({X_0}/{\underline {F}})$
,
![]() $z_2 = z_2({X_0}/{\overline {F}})$
and
$z_2 = z_2({X_0}/{\overline {F}})$
and
![]() $z_0 = z_0({X_0}/{\overline {F}})$
.
$z_0 = z_0({X_0}/{\overline {F}})$
.
As a remark, we note that the accuracy of the estimates in Theorem 3.1 improves when
![]() $F(S) = H(S)/\varphi (S)$
obeys less variation, that is, when one can take a tighter interval in assumption (3.5). We also remark that similar but more accurate estimates follow by using Theorem 2.2 in place of Theorem 2.1 in the above derivation.
$F(S) = H(S)/\varphi (S)$
obeys less variation, that is, when one can take a tighter interval in assumption (3.5). We also remark that similar but more accurate estimates follow by using Theorem 2.2 in place of Theorem 2.1 in the above derivation.
As an example, for which we easily find the above imposed assumptions satisfied and thereby conclude Theorem 3.1, we consider the system
 $$ \begin{align} \begin{aligned} \frac{ds}{d\tau}&=(h(s)-x)s ,\\ \frac{dx}{d\tau}&=m (s-\lambda )x, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{ds}{d\tau}&=(h(s)-x)s ,\\ \frac{dx}{d\tau}&=m (s-\lambda )x, \end{aligned} \end{align} $$
in
![]() $x,s\geq 0$
, supposing parameters
$x,s\geq 0$
, supposing parameters
![]() $m> 0$
,
$m> 0$
,
![]() $\lambda \in (0, 1)$
and where h is given by
$\lambda \in (0, 1)$
and where h is given by
Any standard Rosenzweig–MacArthur predator–prey system can be transformed into a system of type (3.6). In particular, it is equivalent with system (3.1) when (3.2) holds with
![]() $n = 1$
, which can be seen by introducing the nondimensional quantities
$n = 1$
, which can be seen by introducing the nondimensional quantities
 $$ \begin{align*} \begin{aligned} \tau &=\, \int \frac{r K}{A + S(t)} dt, \quad s =\, \frac{S}{K}, \quad x \,=\, \frac{q X}{r K}, \quad a \,=\, \frac{A}{K}, \\ m &=\, \frac{p - d}{r} \quad \text{and} \quad \lambda \,=\, \frac{d A}{(p-d) K}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \tau &=\, \int \frac{r K}{A + S(t)} dt, \quad s =\, \frac{S}{K}, \quad x \,=\, \frac{q X}{r K}, \quad a \,=\, \frac{A}{K}, \\ m &=\, \frac{p - d}{r} \quad \text{and} \quad \lambda \,=\, \frac{d A}{(p-d) K}. \end{aligned} \end{align*} $$
Comparing with the general system (3.1), we identify
![]() $S = s, X = x, F(S) = h(s), \varphi (S) = s, p = m$
and
$S = s, X = x, F(S) = h(s), \varphi (S) = s, p = m$
and
![]() $d = m \lambda $
. Moreover, isoclines are given by
$d = m \lambda $
. Moreover, isoclines are given by
![]() $x = h(s)$
and
$x = h(s)$
and
![]() $s = \lambda $
, and since
$s = \lambda $
, and since
![]() $a < h(s)=(1-s)(s+a) < h(\lambda )$
when
$a < h(s)=(1-s)(s+a) < h(\lambda )$
when
![]() $s < \lambda $
, we obtain (3.5) satisfied in the region
$s < \lambda $
, we obtain (3.5) satisfied in the region
![]() $s < \lambda $
with
$s < \lambda $
with
![]() $\underline {F} = a$
and
$\underline {F} = a$
and
![]() $\overline {F} = h(\lambda )$
. Theorem 3.1 therefore implies the following estimate for the minimal predator biomass,
$\overline {F} = h(\lambda )$
. Theorem 3.1 therefore implies the following estimate for the minimal predator biomass,
![]() $x_{\mathrm {\min }}$
.
$x_{\mathrm {\min }}$
.
Corollary 3.2. Consider a trajectory of system (3.6) starting at
![]() $(x_{\mathrm {\max }},\lambda )$
with
$(x_{\mathrm {\max }},\lambda )$
with
![]() $x_{\mathrm {\max }}> h(\lambda )$
. Suppose that
$x_{\mathrm {\max }}> h(\lambda )$
. Suppose that
![]() $m> 0$
,
$m> 0$
,
![]() $\lambda \in (0, 1)$
and that (3.7) holds. Then, the minimal predator biomass,
$\lambda \in (0, 1)$
and that (3.7) holds. Then, the minimal predator biomass,
![]() $x_{\mathrm {\min }}$
, satisfies
$x_{\mathrm {\min }}$
, satisfies
where
![]() $z_1 = z_1({x_{\mathrm {\max }}}/{a})$
,
$z_1 = z_1({x_{\mathrm {\max }}}/{a})$
,
![]() $z_2 = z_2({x_{\mathrm {\max }}}/{h(\lambda )})$
and
$z_2 = z_2({x_{\mathrm {\max }}}/{h(\lambda )})$
and
![]() $z_0 = z_0({x_{\mathrm {\max }}}/{h(\lambda )})$
.
$z_0 = z_0({x_{\mathrm {\max }}}/{h(\lambda )})$
.
We remark that by shrinking the region
![]() $s < \lambda $
into
$s < \lambda $
into
![]() $s < \lambda ^*$
for some
$s < \lambda ^*$
for some
![]() $0 < \lambda ^* < \lambda $
, we have the better estimates
$0 < \lambda ^* < \lambda $
, we have the better estimates
![]() $a < h(s) < h(\lambda ^*)$
and may, for a trajectory starting at
$a < h(s) < h(\lambda ^*)$
and may, for a trajectory starting at
![]() $(x_0, \lambda ^*)$
, estimate its next intersection with the line
$(x_0, \lambda ^*)$
, estimate its next intersection with the line
![]() $s = \lambda ^*$
at point
$s = \lambda ^*$
at point
![]() $(x_1, \lambda ^*)$
. In particular, we then get Corollary 3.2 but with
$(x_1, \lambda ^*)$
. In particular, we then get Corollary 3.2 but with
![]() $x_{\max } = x_0$
,
$x_{\max } = x_0$
,
![]() $x_{\min } = x_1$
and
$x_{\min } = x_1$
and
![]() $h(\lambda ) = h(\lambda ^*)$
. Furthermore, we observe that the upper estimate is good for small
$h(\lambda ) = h(\lambda ^*)$
. Furthermore, we observe that the upper estimate is good for small
![]() $\lambda $
but becomes less efficient when the value of
$\lambda $
but becomes less efficient when the value of
![]() $\lambda $
increases beyond a. The bounds in Corollary 3.2 will be used by the authors in [Reference Lundström and Söderbacka14] for estimating the size of the unique limit cycle to system (3.6), which is the global attractor when
$\lambda $
increases beyond a. The bounds in Corollary 3.2 will be used by the authors in [Reference Lundström and Söderbacka14] for estimating the size of the unique limit cycle to system (3.6), which is the global attractor when
![]() $2\lambda + a < 1$
.
$2\lambda + a < 1$
.
3.1. Coexistence of predators
As a final remark, we consider the following system similar to (3.1) but allowing for
![]() $n \geq 1$
predators:
$n \geq 1$
predators:
 $$ \begin{align} \begin{aligned} \frac{dS}{dt} &= H(S) - \sum_{i=1}^{n} q_i \varphi_i(S) X_i, \\ \frac{dX_i}{dt} &= p_i \varphi_i(S) X_i - d_i X_i, \quad i = 1, \ldots, n, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{dS}{dt} &= H(S) - \sum_{i=1}^{n} q_i \varphi_i(S) X_i, \\ \frac{dX_i}{dt} &= p_i \varphi_i(S) X_i - d_i X_i, \quad i = 1, \ldots, n, \end{aligned} \end{align} $$
where the nonnegative variable S represents the prey biomass, the nonnegative variables
![]() $X_i$
represent predator biomass,
$X_i$
represent predator biomass,
![]() $\varphi _i$
is nondecreasing,
$\varphi _i$
is nondecreasing,
![]() $\varphi_i(0) = H(0) = 0$
and parameters
$\varphi_i(0) = H(0) = 0$
and parameters
![]() $p_i$
,
$p_i$
,
![]() $q_i$
,
$q_i$
,
![]() $d_i$
are positive.
$d_i$
are positive.
Following [Reference Söderbacka and Petrov22, p. 2], we assume
![]() $p_i> d_i$
. If not, the corresponding predator will die. Using the time change
$p_i> d_i$
. If not, the corresponding predator will die. Using the time change
![]() $\tau = rt$
, where
$\tau = rt$
, where
![]() $\tau $
is the new time, and the variable changes
$\tau $
is the new time, and the variable changes
![]() $s ={S}/{K}, x_i = ({q_i}/{r K}) X_i$
, we transform, when
$s ={S}/{K}, x_i = ({q_i}/{r K}) X_i$
, we transform, when
system (3.8) to the system
 $$ \begin{align} \begin{aligned} \frac{ds}{d\tau} &= \bigg(1 - s - \sum_{i=1}^{n} \frac{x_i}{s + a_i} \bigg) s, \\ \frac{dx_i}{d\tau} &= m_i \frac{s-\lambda_i}{s + a_i}x_i, \quad i = 1, \ldots, n, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{ds}{d\tau} &= \bigg(1 - s - \sum_{i=1}^{n} \frac{x_i}{s + a_i} \bigg) s, \\ \frac{dx_i}{d\tau} &= m_i \frac{s-\lambda_i}{s + a_i}x_i, \quad i = 1, \ldots, n, \end{aligned} \end{align} $$
where
Systems of this type have been studied, see for example, [Reference Osipov and Söderbacka17–Reference Osipov and Söderbacka19, Reference Söderbacka and Petrov22]. In particular, extinction and coexistence results for predators can be found in [Reference Osipov and Söderbacka17, Reference Söderbacka and Petrov22] from which we recall the following statement, giving sufficient conditions for extinction.
Statement 3.3 [Reference Söderbacka and Petrov22, Statement 2].
Let
![]() $L={ \lambda _i (1-\lambda _j) }/{ \lambda _j (1-\lambda _i) }$
and
$L={ \lambda _i (1-\lambda _j) }/{ \lambda _j (1-\lambda _i) }$
and
![]() $\lambda _i>\lambda _j$
. If
$\lambda _i>\lambda _j$
. If
![]() ${a_j > a_i/(L + a_i(L-1))}$
, then the predator i in system (3.9) goes extinct.
${a_j > a_i/(L + a_i(L-1))}$
, then the predator i in system (3.9) goes extinct.
Anyhow, the condition is quite far from necessary, and it is possible to use the results in this work to find sufficient conditions for the opposite, that is, for coexistence of predators. The proof of the statement and similar known proofs for extinction essentially only use the equations for
![]() $x_i$
and the properties of the functions
$x_i$
and the properties of the functions
![]() $\varphi _i$
. The equation for s is only used to make the obvious restriction
$\varphi _i$
. The equation for s is only used to make the obvious restriction
![]() $s<1$
. If we consider the case of two predators, we notice that in the two-dimensional coordinate planes, where one predator is absent, there can be cycles like in the standard Rosenzweig–MacArthur system. The instability of one or two of these cycles can be used to get sufficient conditions for coexistence and, thus, we conjecture that nice estimates, such as those we have produced in this work, could be useful for getting important coexistence conditions contradicting the known exclusion principle.
$s<1$
. If we consider the case of two predators, we notice that in the two-dimensional coordinate planes, where one predator is absent, there can be cycles like in the standard Rosenzweig–MacArthur system. The instability of one or two of these cycles can be used to get sufficient conditions for coexistence and, thus, we conjecture that nice estimates, such as those we have produced in this work, could be useful for getting important coexistence conditions contradicting the known exclusion principle.
Another interesting problem is arising in connection to the bifurcation in system (3.9) examined in [Reference López-Nieto, Lappicy, Vassena, Stuke and Dai12]. There, under certain conditions, they conclude cyclic coexistence of the predators for parameters near to the case
![]() $\lambda _1=\lambda _2$
, where there is a cycle only in one of the coordinate planes. We conjecture that for this cycle, our estimates can be used to prove its instability and, thus, coexistence for a parameter range after the bifurcation. We observe that in all these cases, we suppose to use the results only far beyond the bifurcation to cycle of the equilibrium, when the cycles are big, and parameters
$\lambda _1=\lambda _2$
, where there is a cycle only in one of the coordinate planes. We conjecture that for this cycle, our estimates can be used to prove its instability and, thus, coexistence for a parameter range after the bifurcation. We observe that in all these cases, we suppose to use the results only far beyond the bifurcation to cycle of the equilibrium, when the cycles are big, and parameters
![]() $a_i$
and
$a_i$
and
![]() $\lambda _i$
are small. Finally, we remark that the behaviour for small prey biomass on the cycle can play an important role in determining the stability (see [Reference Osipov and Söderbacka19] and references therein) and, thus, estimates of the limit cycle for small prey, such as those in Theorem (3.1), obtained by Theorem 2.1, may be useful.
$\lambda _i$
are small. Finally, we remark that the behaviour for small prey biomass on the cycle can play an important role in determining the stability (see [Reference Osipov and Söderbacka19] and references therein) and, thus, estimates of the limit cycle for small prey, such as those in Theorem (3.1), obtained by Theorem 2.1, may be useful.
4. Conclusions
Lotka–Volterra integrals have been frequently used in theoretical biology over nearly 100 years. One frequent application is construction of Lyapunov functions for trapping trajectories of biological systems. With the aim of estimating Lotka–Volterra integrals, we have used Padé approximations of the logarithm to derive simple analytical bounds for solutions of the equation
![]() $x - \ln x = y -\ln y$
. In Theorem 2.1, we derive our simplest bounds, and in Theorem 2.2, we apply higher order Padé approximations and derive some sharper bounds. We show how our theorems imply estimates for the Lambert W function in Corollaries 2.3 and 2.4, and Figures 2 and 3 show some comparisons with existing approximations of the Lambert W function. Moreover, in Theorem 3.1, we show how to apply our theorems for trapping trajectories of more general predator–prey systems, including, for example, Rosenzweig–MacArthur equations (see Corollary 3.2). As a final remark, we discuss possible applications of our estimates in systems allowing for the existence of several predators, for example, we conjecture that our estimates can be useful when investigating stability and coexistence of predators in systems on the form (3.8).
$x - \ln x = y -\ln y$
. In Theorem 2.1, we derive our simplest bounds, and in Theorem 2.2, we apply higher order Padé approximations and derive some sharper bounds. We show how our theorems imply estimates for the Lambert W function in Corollaries 2.3 and 2.4, and Figures 2 and 3 show some comparisons with existing approximations of the Lambert W function. Moreover, in Theorem 3.1, we show how to apply our theorems for trapping trajectories of more general predator–prey systems, including, for example, Rosenzweig–MacArthur equations (see Corollary 3.2). As a final remark, we discuss possible applications of our estimates in systems allowing for the existence of several predators, for example, we conjecture that our estimates can be useful when investigating stability and coexistence of predators in systems on the form (3.8).
Acknowledgements
We would like to thank two anonymous reviewers for valuable comments and suggestions which really helped us to improve this work.