Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-29T13:41:59.870Z Has data issue: false hasContentIssue false
  • English
  • Français

EPIDEMIC DYNAMICS ON RANDOM AND SCALE-FREE NETWORKS

Published online by Cambridge University Press:  30 January 2013

J. BARTLETT  and
M. J. PLANK
J. BARTLETT
Affiliation:
Department of Mathematics and Statistics, University of Canterbury, Christchurch, New Zealand
M. J. PLANK*
Affiliation:
Department of Mathematics and Statistics, University of Canterbury, Christchurch, New Zealand
*
✉michael.plank@canterbury.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Random networks were first used to model epidemic dynamics in the 1950s, but in the last decade it has been realized that scale-free networks more accurately represent the network structure of many real-world situations. Here we give an analytical and a Monte Carlo method for approximating the basic reproduction number 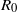${R}_{0} $ of an infectious agent on a network. We investigate how final epidemic size depends on 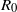${R}_{0} $ and on network density in random networks and in scale-free networks with a Pareto exponent of 3. Our results show that: (i) an epidemic on a random network has the same average final size as an epidemic in a well-mixed population with the same value of ${R}_{0} $; (ii) an epidemic on a scale-free network has a larger average final size than in an equivalent well-mixed population if 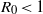${R}_{0} \lt 1$, and a smaller average final size than in a well-mixed population if 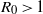${R}_{0} \gt 1$; (iii) an epidemic on a scale-free network spreads more rapidly than an epidemic on a random network or in a well-mixed population.

Keywords

degree distributionPareto distributionpower lawrandom graphSIR modelsuperspreaders

MSC classification

Secondary: 92D40: Ecology
Type
Research Article
Information
The ANZIAM Journal , Volume 54 , Issue 1-2 , October 2012 , pp. 3 - 22
Copyright
Copyright ©2013 Australian Mathematical Society 

References

Albert, R. and Barabási, A.-L., “Statistical mechanics of complex networks”, Rev. Modern Phys. 74 (2002) 47–97; doi:10.1103/RevModPhys.74.47.CrossRefGoogle Scholar
Alderson, D., Chang, H., Roughan, M., Uhlig, S. and Willinger, W., “The many facets of internet topology and traffic”, Net. Heterog. Media 1 (2006) 569–600; doi:10.3934/nhm.2006.1.569.CrossRefGoogle Scholar
Anderson, R. M. and May, R. M., Infectious diseases of humans: dynamics and control (Oxford University Press, Oxford, 1991).CrossRefGoogle Scholar
Andreasen, V., Lin, J. and Levin, S. A., “The dynamics of cocirculating influenza strains conferring partial cross-immunity”, J. Math. Biol. 35 (1997) 825–842; doi:10.1007/s002850050079.CrossRefGoogle ScholarPubMed
Barabási, A.-L. and Albert, R., “Emergence of scaling in random networks”, Science 286 (1999) 509–512; doi:10.1126/science.286.5439.509.CrossRefGoogle ScholarPubMed
Barthélemy, M., Barrat, A., Pastor-Satorras, R. and Vespignani, A., “Velocity and hierarchical spread of epidemic outbreaks in scale-free networks”, Phys. Rev. Lett. 92 (2004) 178701; doi:10.1103/PhysRevLett.92.178701.CrossRefGoogle ScholarPubMed
Boguñá, M., Pastor-Satorras, R. and Vespignani, A., “Absence of epidemic threshold in scale-free networks with degree correlations”, Phys. Rev. Lett. 90 (2003) 028701; doi:10.1103/PhysRevLett.90.028701.CrossRefGoogle ScholarPubMed
Brauer, F. and van den Driessche, P., “Models for transmission of disease with immigration of infectives”, Math. Biosci. 171 (2001) 143–154; doi:10.1016/S0025-5564(01)00057-8.CrossRefGoogle ScholarPubMed
Callaway, D. S., Newman, M. E. J., Strogatz, S. H. and Watts, D. J., “Network robustness and fragility: percolation on random graphs”, Phys. Rev. Lett. 85 (2000) 5468–5471; doi:10.1103/PhysRevLett.85.5468.CrossRefGoogle ScholarPubMed
David, T., van Kempen, T., Huang, H. and Wilson, P., “The geometry and dynamics of binary trees”, Math. Comput. Simulation 81 (2011) 1464–1481; doi:10.1016/j.matcom.2010.04.020.CrossRefGoogle Scholar
Diekmann, O. and Heesterbeek, J. A. P., Mathematical epidemiology of infectious diseases: model building, analysis and interpretation (John Wiley & Sons, Chichester, 2000).Google Scholar
Dorogovtsev, S. N., Mendes, J. F. F. and Samukhin, A. N., “Structure of growing networks with preferential linking”, Phys. Rev. Lett. 85 (2000) 4633–4636; doi:10.1103/PhysRevLett.85.4633.CrossRefGoogle ScholarPubMed
Eguíluz, V. M. and Klemm, K., “Epidemic threshold in structured scale-free networks”, Phys. Rev. Lett. 89 (2002) 108701; doi:10.1103/PhysRevLett.89.108701.CrossRefGoogle ScholarPubMed
Erdős, P. and Rényi, A., “On random graphs I”, Publ. Math. Debrecen 6 (1959) 290–297.CrossRefGoogle Scholar
Fu, X., Small, M., Walker, D. M. and Zhang, H., “Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization”, Phys. Rev. E 77 (2008) 036113; doi:10.1103/PhysRevE.77.036113.CrossRefGoogle ScholarPubMed
Gillespie, D. T., “Exact stochastic simulation of coupled chemical reactions”, J. Phys. Chem. 81 (1977) 2340–2361; doi:10.1021/j100540a008.CrossRefGoogle Scholar
Hufnagel, L., Brockmann, D. and Geisel, T., “Forecast and control of epidemics in a globalized world”, Proc. Natl. Acad. Sci. 101 (2004) 15124–15129; doi:10.1073/pnas.0308344101.CrossRefGoogle Scholar
Jacquez, J. A. and Simon, C. P., “The stochastic SI model with recruitment and deaths I. Comparison with the closed SIS model”, Math. Biosci. 117 (1993) 77–125; doi:10.1016/0025-5564(93)90018-6.CrossRefGoogle ScholarPubMed
James, A., Pitchford, J. W. and Plank, M. J., “An event-based model of superspreading in epidemics”, Proc. R. Soc. Lond. B 274 (2007) 741–747; doi:10.1098/rspb.2006.0219.Google ScholarPubMed
James, A., Pitchford, J. W. and Plank, M. J., “Disentangling nestedness from models of ecological complexity”, Nature 487 (2012) 227–230; doi:10.1038/nature11214.CrossRefGoogle ScholarPubMed
Keeling, M. J., “The effects of local spatial structure on epidemiological invasions”, Proc. R. Soc. Lond. B 266 (1999) 859–867; doi:10.1098/rspb.1999.0716.CrossRefGoogle ScholarPubMed
Kermack, W. O. and McKendrick, A. G., “A contribution to the mathematical theory of epidemics”, Proc. R. Soc. Lond. A 115 (1927) 700–721; doi:10.1098/rspa.1927.0118.Google Scholar
Kiss, I. Z., Green, D. M. and Kao, R. R., “Disease contact tracing in random and clustered networks”, Proc. R. Soc. Lond. B 272 (2005) 1407–1414; doi:10.1098/rspb.2005.3092.Google ScholarPubMed
Kiss, I. Z., Green, D. M. and Kao, R. R., “Infectious disease control using contact tracing in random and scale-free networks”, J. Roy. Soc. Interface 3 (2006) 55–62; doi:10.1098/rsif.2005.0079.CrossRefGoogle ScholarPubMed
Liu, J.-G., Wang, Z.-T. and Dang, Y.-Z., “Optimization of robustness of scale-free network to random and targeted attacks”, Modern Phys. Lett. B 19 (2005) 785–792; doi:10.1142/S0217984905008773.CrossRefGoogle Scholar
Lloyd, A. L., “Realistic distributions of infectious periods in epidemic models: changing patterns of persistence and dynamics”, Theor. Populat. Biol. 60 (2001) 59–71; doi:10.1006/tpbi.2001.1525.CrossRefGoogle ScholarPubMed
Lloyd-Smith, J. O., Schreiber, S. J., Kopp, P. E. and Getz, W. M., “Superspreading and the effect of individual variation on disease emergence”, Nature 438 (2005) 355–359; doi:10.1038/nature04153.CrossRefGoogle ScholarPubMed
Madar, N., Kalisky, T., Cohen, T., ben-Avraham, D. and Havlin, S., “Immunization and epidemic dynamics in complex networks”, Eur. Phys. J. B 38 (2004) 269–276; doi:10.1140/epjb/e2004-00119-8.CrossRefGoogle Scholar
May, R. M. and Lloyd, A. L., “Infection dynamics on scale-free networks”, Phys. Rev. E 64 (2001) 066112; doi:10.1103/PhysRevE.64.066112.CrossRefGoogle ScholarPubMed
Newman, M. E. J., “Power laws, Pareto distributions and Zipf’s law”, Contemp. Phys. 46 (2005) 323–351; doi:10.1080/00107510500052444.CrossRefGoogle Scholar
Rado, R., “Universal graphs and universal functions”, Acta. Arith. 9 (1964) 331–340.CrossRefGoogle Scholar
Rezende, E. L., Lavabre, J. E., Guimarães, P. R., Jordano, P. and Bascompte, J., “Non-random coextinctions in phylogenetically structured mutualistic networks”, Nature 448 (2007) 925–928; doi:10.1038/nature05956.CrossRefGoogle ScholarPubMed
Roberts, M. G., “A Kermack–McKendrick model applied to an infectious disease in a natural population”, Math. Med. Biol. 16 (1999) 319–332; doi:10.1093/imammb16.4.319.CrossRefGoogle Scholar
Roberts, M. G., “The pluses and minuses of ${ \mathcal{R} }_{0} $”, J. Roy. Soc. Interface 4 (2007) 949–961; doi:10.1098/rsif.2007.1031.CrossRefGoogle Scholar
Roberts, M. G. and Heesterbeek, J. A. P., “A new method for estimating the effort required to control an infectious disease”, Proc. R. Soc. Lond. B 270 (2003) 1359–1364; doi:10.1098/rspb.2003.2339.CrossRefGoogle ScholarPubMed
Roberts, M. G. and Tobias, M. I., “Predicting and preventing measles epidemics in New Zealand: application of a mathematical model”, Epidemiol. Infect. 124 (2000) 279–287; doi:10.1017/S0950268899003556.CrossRefGoogle ScholarPubMed
Ross, J. V., “Invasion of infectious diseases in finite homogeneous populations”, J. Theoret. Biol. 289 (2011) 83–89; doi:10.1016/j.jtbi.2011.08.035.CrossRefGoogle ScholarPubMed
Travers, J. and Milgram, S., “An experimental study of the small world problem”, Sociometry 32 (1969) 425–443; doi:10.2307/2786545.CrossRefGoogle Scholar
Watts, D. J. and Strogatz, S. H., “Collective dynamics of ‘small-world’ networks”, Nature 393 (1988) 440–442; doi:10.1038/30918.CrossRefGoogle Scholar
Zhou, Y. and Liu, H., “Stability of periodic solutions for an SIS model with pulse vaccination”, Math. Comput. Modelling 38 (2003) 299–308; doi:10.1016/S0895-7177(03)90088-4.CrossRefGoogle Scholar