Article contents
On a transformation of the weighted compound Poisson process
Published online by Cambridge University Press: 29 August 2014
Extract
We are using the following terminology—essentially following Feller:
a) Compound Poisson Variable
This is a random variable 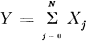
where X1, X2, … Xn, … independent, identically distributed (X0 = o) and N a Poisson counting variable
hence

(common) distribution function of the Xj with j ≠ 0 or in the language of characteristic functions
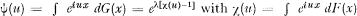
b) Weighted Compound Poisson Variable
This is a random variable Z obtained from a class of Compound Poisson Variables by weighting over λ with a weight function S(λ)
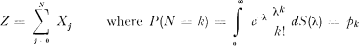
hence

or in the language of characteristic functions

Let [Z(t); t ≥ o] be a homogeneous Weighted Compound Poisson Process. The characteristic function at the time epoch t reads then

It is most remarkable that in many instances φt(u) can be represented as a (non weighted) Compound Poisson Variable. Our main result is given as a theorem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1971
References
- 2
- Cited by

