No CrossRef data available.
Article contents
CHARACTERISTIC POLYNOMIALS OF SIMPLE ORDINARY ABELIAN VARIETIES OVER FINITE FIELDS
Part of:
Abelian varieties and schemes
Arithmetic problems. Diophantine geometry
Arithmetic algebraic geometry
Published online by Cambridge University Press: 19 February 2021
Abstract
We provide an easy method for the construction of characteristic polynomials of simple ordinary abelian varieties 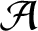 ${{\mathcal A}}$ of dimension g over a finite field
${{\mathcal A}}$ of dimension g over a finite field 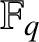 ${{\mathbb F}}_q$, when
${{\mathbb F}}_q$, when 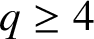 $q\ge 4$ and
$q\ge 4$ and 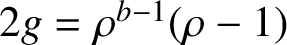 $2g=\rho ^{b-1}(\rho -1)$, for some prime
$2g=\rho ^{b-1}(\rho -1)$, for some prime 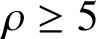 $\rho \ge 5$ with
$\rho \ge 5$ with 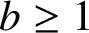 $b\ge 1$. Moreover, we show that
$b\ge 1$. Moreover, we show that 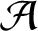 ${{\mathcal A}}$ is absolutely simple if
${{\mathcal A}}$ is absolutely simple if 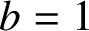 $b=1$ and g is prime, but
$b=1$ and g is prime, but 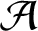 ${{\mathcal A}}$ is not absolutely simple for any prime
${{\mathcal A}}$ is not absolutely simple for any prime 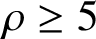 $\rho \ge 5$ with
$\rho \ge 5$ with 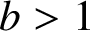 $b>1$.
$b>1$.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 391 - 397
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
References
Deligne, P., ‘La conjecture de Weil. I’, Inst. Hautes Études Sci. Publ. Math. 43 (1974), 273–307.10.1007/BF02684373CrossRefGoogle Scholar
DiPippo, S. A. and Howe, E. W., ‘Real polynomials with all roots on the unit circle and abelian varieties over finite fields’, J. Number Theory 73(2) (1998), 426–450.10.1006/jnth.1998.2302CrossRefGoogle Scholar
Dwork, B., ‘On the rationality of the zeta function of an algebraic variety’, Amer. J. Math. 82 (1960), 631–648.10.2307/2372974CrossRefGoogle Scholar
Grothendieck, A., ‘Formule de Lefschetz et rationalité des fonctions
 $L$
’, Séminaire Bourbaki, 9, Exp. No. 279 (Société Mathématique de France, Paris, 1995), 41–55.Google Scholar
$L$
’, Séminaire Bourbaki, 9, Exp. No. 279 (Société Mathématique de France, Paris, 1995), 41–55.Google Scholar
Guerrier, W. J., ‘The factorization of the cyclotomic polynomials mod
 $p$
’, Amer. Math. Monthly 75 (1968) 46.CrossRefGoogle Scholar
$p$
’, Amer. Math. Monthly 75 (1968) 46.CrossRefGoogle Scholar
Haloui, S., ‘The characteristic polynomials of abelian varieties of dimensions 3 over finite fields’, J. Number Theory 130(12) (2010), 2745–2752.10.1016/j.jnt.2010.06.008CrossRefGoogle Scholar
Haloui, S. and Singh, V., ‘The characteristic polynomials of abelian varieties of dimension 4 over finite fields’, Arithmetic, Geometry, Cryptography and Coding Theory, Contemporary Mathematics, 574 (American Mathematical Society, Providence, RI, 2012), 59–68.CrossRefGoogle Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, 52 (Springer-Verlag,
New York, 1977).10.1007/978-1-4757-3849-0CrossRefGoogle Scholar
Honda, T., ‘Isogeny classes of abelian varieties over finite fields’, J. Math. Soc. Japan 20 (1968), 83–95.10.2969/jmsj/02010083CrossRefGoogle Scholar
Howe, E. W., ‘Principally polarized ordinary abelian varieties over finite fields’, Trans. Amer. Math. Soc. 347 (1995), 2361–2401.CrossRefGoogle Scholar
Howe, E. W. and Zhu, H. J., ‘On the existence of absolutely simple abelian varieties of a given dimension over an arbitrary field’, J. Number Theory 92(1) (2002), 139–163.10.1006/jnth.2001.2697CrossRefGoogle Scholar
Lakatos, P. and Losonczi, L., ‘Circular interlacing with reciprocal polynomials’, Math. Inequal. Appl. 10(4) (2007), 761–769.Google Scholar
Lehmer, D. H., ‘Quasi-cyclotomic polynomials’, Amer. Math. Monthly 39(7) (1932), 383–389.10.1080/00029890.1932.11987335CrossRefGoogle Scholar
Maisner, D. and Nart, E., ‘Abelian surfaces over finite fields as Jacobians’, with an appendix by Howe, Everett W., Experiment. Math. 11(3) (2002), 321–337.10.1080/10586458.2002.10504478CrossRefGoogle Scholar
Rück, H., ‘Abelian surfaces and Jacobian varieties over finite fields’, Compositio Math. 76(3) (1990), 351–366.Google Scholar
Singh, V., McGuire, G. and Zaytsev, A., ‘Classification of characteristic polynomials of simple supersingular abelian varieties over finite fields’, Funct. Approx. Comment. Math. 51(2) (2014), 415–436.Google Scholar
Tate, J., ‘Endomorphisms of abelian varieties over finite fields’, Invent. Math. 2 (1966) 134–144.CrossRefGoogle Scholar
Waterhouse, W. C., ‘Abelian varieties over finite fields’, Ann. Sci. École Norm. Sup. (4) 2 (1969), 521–560.CrossRefGoogle Scholar
Waterhouse, W. C. and Milne, J. S., ‘Abelian varieties over finite fields’, Proc. Sympos. Pure Math. 20 (1971), 53–64.10.1090/pspum/020/0314847CrossRefGoogle Scholar
Weil, A., ‘Numbers of solutions of equations in finite fields’, Bull. Amer. Math. Soc. 55 (1949), 497–508
10.1090/S0002-9904-1949-09219-4CrossRefGoogle Scholar


