Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-30T16:18:42.907Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE REGULARITY INDEX OF FAT POINTS WHOSE SUPPORT IS CONTAINED IN A LINEAR PROPER SUBSPACE

Part of: Cycles and subschemes Commutative algebra: Homological methods

Published online by Cambridge University Press:  20 June 2025

PHAN VAN THIEN Open the ORCID record for PHAN VAN THIEN [Opens in a new window]
PHAN VAN THIEN*
Affiliation:
Department of Mathematics, University of Education, Hue University , Hue City, Vietnam
*
e-mail: pvthien@hueuni.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the conjecture of Franceschini and Lorenzini [‘Fat points of 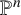$\mathbb P^n$ whose support is contained in a linear proper subspace’, J. Pure and Appl. Algebra 160 (2001), 169–182] about the regularity index of fat points of 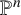$\mathbb P^n$ whose support is contained in a linear proper subspace.

Keywords

fat pointsregularity index

MSC classification

Primary: 14C20: Divisors, linear systems, invertible sheaves
Secondary: 13D40: Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Benedetti, B., Fatabbi, G. and Lorenzini, A., ‘Segre’s bound and the case of $n+2$ fat points of ${P}^n$ ’, Comm. Algebra 40 (2012), 395–403.10.1080/00927872.2010.529093CrossRefGoogle Scholar
Catalisano, M. V., Trung, N. V. and Valla, G., ‘A sharp bound for the regularity index of fat points in general position’, Proc. Amer. Math. Soc. 118 (1993), 717–724.10.1090/S0002-9939-1993-1146859-0CrossRefGoogle Scholar
Davis, E. D. and Geramita, A. V., ‘The Hilbert function of a special class of 1-dimensional Cohen–Macaulay graded algebras’, in: The Curves Seminar at Queen’s, Queen’s Papers in Pure and Applied Mathematics, 67 (ed. Geramita, A. V.) (Queen’s University, Kingston, Ontario, 1984), 1–29.Google Scholar
Fatabbi, G., ‘Regularity index of fat points in the projective plane’, J. Algebra 170 (1994), 916–928.10.1006/jabr.1994.1370CrossRefGoogle Scholar
Fatabbi, G. and Lorenzini, A., ‘On a sharp bound for the regularity index of any set of fat points’, J. Pure Appl. Algebra 161 (2001), 91–111.10.1016/S0022-4049(00)00083-9CrossRefGoogle Scholar
Franceschini, S. and Lorenzini, A., ‘Fat points of ${\mathbb{P}}^n$ whose support is contained in a linear proper subspace’, J. Pure Appl. Algebra 160 (2001), 169–182.10.1016/S0022-4049(00)00084-0CrossRefGoogle Scholar
Nagel, U. and Trok, B., ‘Segre’s regularity bound for fat point schemes’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) XX (2020), 217–237.Google Scholar
Segre, B., ‘Alcune questioni su insiemi finiti di punti in geometria algebrica’, Atti. Convegno. Intern. di Torino 1960 (1961), 15–33.Google Scholar
Thien, P. V., ‘Segre bound for the regularity index of fat points in ${\mathbb{P}}^3$ ’, J. Pure Appl. Algebra 151 (2000), 197–214.10.1016/S0022-4049(99)00055-9CrossRefGoogle Scholar
Thien, P. V. and Sinh, T. N., ‘On the regularity index of s fat points not on a linear $\left(r-1\right)$ -space, $s\le r+3$ ’, Comm. Algebra 45 (2017), 4123–4138.10.1080/00927872.2016.1222395CrossRefGoogle Scholar