Hostname: page-component-5d84bcc8dc-zr99j Total loading time: 0 Render date: 2026-09-11T21:34:58.130Z Has data issue: false hasContentIssue false
  • English
  • Français

UPPER BOUNDS ON THE SEMITOTAL FORCING NUMBER OF GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  19 June 2023

YI-PING LIANG Open the ORCID record for YI-PING LIANG [Opens in a new window] ,
JIE CHEN Open the ORCID record for JIE CHEN [Opens in a new window]  and
SHOU-JUN XU Open the ORCID record for SHOU-JUN XU [Opens in a new window]
YI-PING LIANG*
Affiliation:
School of Mathematics and Statistics, Gansu Center for Applied Mathematics, Lanzhou University, Lanzhou, Gansu 730000, PR China
JIE CHEN
Affiliation:
School of Mathematics and Statistics, Gansu Center for Applied Mathematics, Lanzhou University, Lanzhou, Gansu 730000, PR China e-mail: chenjie21@lzu.edu.cn
SHOU-JUN XU
Affiliation:
School of Mathematics and Statistics, Gansu Center for Applied Mathematics, Lanzhou University, Lanzhou, Gansu 730000, PR China e-mail: shjxu@lzu.edu.cn
*
e-mail: liangyp18@lzu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a graph with no isolated vertex. A semitotal forcing set of G is a (zero) forcing set S such that every vertex in S is within distance 2 of another vertex of S. The semitotal forcing number 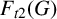$F_{t2}(G)$ is the minimum cardinality of a semitotal forcing set in G. In this paper, we prove that it is NP-complete to determine the semitotal forcing number of a graph. We also prove that if 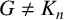$G\neq K_n$ is a connected graph of order 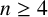$n\geq 4$ with maximum degree 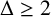$\Delta \geq 2$, then 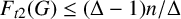$F_{t2}(G)\leq (\Delta-1)n/\Delta$, with equality if and only if either 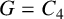$G=C_{4}$ or 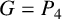$G=P_{4}$ or 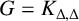$G=K_{\Delta ,\Delta }$.

Keywords

semitotal forcing numberNP-completeextremal graphupper bound

MSC classification

Primary: 05C69: Dominating sets, independent sets, cliques

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 2 , April 2024 , pp. 177 - 185
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work is supported by National Natural Science Foundation of China (Grants Nos. 12071194, 11571155).

References

Aazami, A., Hardness Results and Approximation Algorithms for Some Problems on Graphs, PhD thesis, University of Waterloo, 2008.Google Scholar
AIM Minimum Rank–Special Graphs Work Group (Barioli, F., Barrett, W., Butler, S., Cioabǎ, S., Cvetković, D., Fallat, S., Godsil, C., Haemers, W., Hogben, L., Mikkelson, R., Narayan, S., Pryporova, O., Sciriha, I., So, W., Stevanović, D., van der Holst, H., Meulen, K. Vander and Wangsness, A.), ‘Zero forcing sets and the minimum rank of graphs’, Linear Algebra Appl. 428 (2008), 1628–1648.Google Scholar
Amos, D., Caro, Y., Davila, R. and Pepper, R., ‘Upper bounds on the $k$ -forcing number of a graph’, Discrete Appl. Math. 181 (2015), 1–10.CrossRefGoogle Scholar
Caro, Y. and Pepper, R., ‘Dynamic approach to $k$ -forcing’, Theory Appl. Graphs 2(2) (2015), Article no. 2.Google Scholar
Chekuri, C. and Korula, N., ‘A graph reduction step preserving element-connectivity and applications’, in: Automata, Languages and Programming, Lecture Notes in Computer Science, 5555 (eds. Albers, S., Marchetti-Spaccamela, A., Matias, Y., Nikoletseas, S. and Thomas, W.) (Springer, Berlin–Heidelberg, 2009), 254–265.CrossRefGoogle Scholar
Chen, Q., ‘On the semitotal forcing number of a graph’, Bull. Malays. Math. Sci. Soc. 45 (2022), 1409–1424.CrossRefGoogle Scholar
Davila, R. and Henning, M., ‘On the total forcing number of a graph’, Discrete Appl. Math. 257 (2019), 115–127.CrossRefGoogle Scholar
Davila, R. and Kenter, F., ‘Bounds for the zero forcing number of graphs with large girth’, Theory Appl. Graphs 2(2) (2015), Article no. 1.Google Scholar
Gentner, M., Penso, L., Rautenbach, D. and Souza, U., ‘Extremal values and bounds for the zero forcing number’, Discrete Appl. Math. 213 (2016) 196–200.CrossRefGoogle Scholar
Liang, Y.-P. and Xu, S.-J., ‘On graphs maximizing the zero forcing number’, Discrete Appl. Math. 334 (2023), 81–90.CrossRefGoogle Scholar
Lu, L., Wu, B. and Tang, Z., ‘Proof of a conjecture on the zero forcing number of a graph’, Discrete Appl. Math. 213 (2016), 223–237.CrossRefGoogle Scholar