No CrossRef data available.
Article contents
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
Part of:
Normed linear spaces and Banach spaces; Banach lattices
Selfadjoint operator algebras
Linear spaces and algebras of operators
Published online by Cambridge University Press: 07 February 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let  $n$ be a positive integer. A
$n$ be a positive integer. A 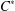 $C^{\ast }$-algebra is said to be
$C^{\ast }$-algebra is said to be  $n$-subhomogeneous if all its irreducible representations have dimension at most
$n$-subhomogeneous if all its irreducible representations have dimension at most  $n$. We give various approximation properties characterising
$n$. We give various approximation properties characterising  $n$-subhomogeneous
$n$-subhomogeneous 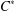 $C^{\ast }$-algebras.
$C^{\ast }$-algebras.
Keywords
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 328 - 337
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by a Polish National Science Centre grant under the contract number DEC2012/06/A/ST1/00256 and by the grant H2020-MSCA-RISE-2015-691246-QUANTUM DYNAMICS. The second author was supported by Mongolian Science and Technology Foundation grants SSA-012/2016 and ShuSs-2017/76.
References
Blackadar, B., Operator Algebras: Theory of C
∗ -Algebras and von Neumann Algebras, Encyclopaedia of Mathematical Sciences, 122 [Operator Algebras and Non-commutative Geometry III] (Springer, Berlin, 2006).Google Scholar
Brown, N. P. and Ozawa, N.,
C
∗ -Algebras and Finite-dimensional Approximations, Graduate Studies in Mathematics, 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Choi, M. D., ‘Positive linear maps on C
∗ -algebras’, Canad. J. Math.
24 (1972), 520–529.Google Scholar
De Cannière, J. and Haagerup, U., ‘Multipliers of the Fourier algebras of some simple Lie groups and their discrete subgroups’, Amer. J. Math.
107(2) (1985), 455–500.10.2307/2374423Google Scholar
Huruya, T. and Tomiyama, J., ‘Completely bounded maps of C
∗ -algebras’, J. Operator Theory
10(1) (1983), 141–152.Google Scholar
Loebl, R. I., ‘Contractive linear maps on C
∗ -algebras’, Michigan Math. J.
22(4) (1976), 361–366.Google Scholar
Pedersen, G. K.,
C
∗ -Algebras and Their Automorphism Groups, London Mathematical Society Monographs, 14 (Academic Press [Harcourt Brace Jovanovich], London, 1979).Google Scholar
Smith, R. R., ‘Completely bounded maps between C
∗ -algebras’, J. Lond. Math. Soc. (2)
27(1) (1983), 157–166.10.1112/jlms/s2-27.1.157Google Scholar
Smith, R. R., ‘Completely contractive factorizations of C
∗ -algebras’, J. Funct. Anal.
64(3) (1985), 330–337.Google Scholar
Stinespring, W. F., ‘Positive functions on C
∗ -algebras’, Proc. Amer. Math. Soc.
6 (1955), 211–216.Google Scholar
Takesaki, M., Theory of Operator Algebras. I, Encyclopaedia of Mathematical Sciences, 124 (Springer, Berlin, 2002), reprint of the first (1979) edition.Google Scholar
Tomiyama, J., ‘On the difference of n-positivity and complete positivity in C
∗ -algebras’, J. Funct. Anal.
49(1) (1982), 1–9.Google Scholar
Tomiyama, J. and Takesaki, M., ‘Applications of fibre bundles to the certain class of C
∗ -algebras’, Tôhoku Math. J. (2)
13 (1961), 498–522.Google Scholar
Walter, M. E., ‘Algebraic structures determined by 3 by 3 matrix geometry’, Proc. Amer. Math. Soc.
131(7) (2003), 2129–2131 (electronic).Google Scholar

