Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-27T02:47:29.403Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterisation of Embeddings in Lorentz Spaces

Published online by Cambridge University Press:  17 April 2009

A. Gogatishvili ,
M. Johansson ,
C. A. Okpoti  and
L.-E. Persson
A. Gogatishvili
Affiliation:
Mathematical Institute, Academy of Sciences of the Czech Republic, Zitná 25, 11567 Prague 1, Czech Republic e-mail: gogatish@math.cas.cz
M. Johansson
Affiliation:
Department of Mathematics, Lulea University of Technology, SE-971 87, Lulea, Sweden e-mail: maria.l.johansson@ltu.se, cao@ltu.se, larserik@sm.luth.se
C. A. Okpoti
Affiliation:
Department of Mathematics, University of Education, P.O. Box 25, Winneba, Ghana e-mail: okpoticao@yahoo.com, cao@ltu.se
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Some new integral conditions characterising the embedding ∧p(v) ↪ Γq(w), 0 < p, q ≤ ∞ are presented, including proofs also for the cases (i) p = ∞, 0 < q < ∞, (ii) q = ∞, I < p < ∞ and (iii) p = q = ∞. Only one condition is necessary for each case which means that our conditions are different from and simpler than other corresponding conditions in the literature. We even prove our results in a more general frame namely when the space Γq(w) is replaced by the more general space . 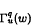In our proof we use a technique of discretisation and anti-discretisation developed by A. Gogatishvili and L. Pick, where they considered the opposite embedding.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 76 , Issue 1 , August 2007 , pp. 69 - 92
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Ariño, M. and Muckenhoupt, B., ‘Maximal functions on classical Lorentz spaces and Hardy's inequality with weights for non-increasing functions’, Trans. Amer. Math. Soc. 320 (1990), 727–735.Google Scholar
[2]Bennett, C. and Sharpley, R., Interpolation of operators, Pure and Applied Mathematics 129 (Academic Press, Boston, 1988).Google Scholar
[3]Carro, M., del Amo, A. García and Soria, J., ‘Weak-type weights and normable Lorentz spaces’, Proc. Amer. Math. Soc. 124 (1996), 849–857.CrossRefGoogle Scholar
[4]Carro, M. and Soria, J., ‘Weighted Lorentz spaces and the Hardy operator’, J. Funct. Anal. 112 (1993), 480–494.CrossRefGoogle Scholar
[5]Carro, M. and Soria, J., ‘Boundedness of some integral operators’, Canad. J. Math. 45 (1993), 1155–1166.CrossRefGoogle Scholar
[6]Carro, M. and Soria, J., ‘The Hardy-Littlewood maximal function and weighted Lorentz spaces’, J. London Math. Soc. 55 (1997), 146–158.CrossRefGoogle Scholar
[7]Carro, M., Soria, J., Pick, L. and Stepanov, V.D., ‘On embeddings between classical Lorentz spaces’, Math. Ineq. Appl. 4 (2001), 397–428.Google Scholar
[8]Gogatishvili, A. and Pick, L., ‘Duality principles and reduction theorems’, Math. Ineq. Appl. 3 (2000), 539–558.Google Scholar
[9]Gogatishvili, A. and Pick, L., ‘Discretization and anti-discretization of rearrangement-invariant norms’, Publ. Mat. 47 (2003), 311–358.CrossRefGoogle Scholar
[10]Gogatishvili, A. and Pick, L., ‘Embeddings and duality theory for weak clasical Lorents spaces’, Canad. Math. Bull. 49 (2006), 82–95.CrossRefGoogle Scholar
[11]Gol'dman, M.L., ‘Sharp estimates for the norms of Hardy-type operators on the cones of quasimonotone functions’, Proc. Steklov Inst. Math. 232 (2001), 1–29.Google Scholar
[12]Gol'dman, M.L., Heinig, H.P. and Stepanov, V.D., ‘On the principle of duality in Lorentz spaces’, Canad. J. Math. 48 (1996), 959–979.CrossRefGoogle Scholar
[13]Lorentz, G.G., ‘On the theory of spaces Λ’, Pacific J. Math. 1 (1951), 411–429.CrossRefGoogle Scholar
[14]Opic, B. and Kufner, A., Hardy-type inequalities, Pitman Research Notes in Mathematics (Longman Sci. & Tech., Harlow, 1990).Google Scholar
[15]Sawyer, E., ‘Boundedness of classical operators on classical Lorentz spaces’, Studia Math. 96 (1990), 145–158.CrossRefGoogle Scholar
[16]Sinnamon, G., ‘Spaces defined by level functions and their duals’, Studia Math. 111 (1994), 19–52.CrossRefGoogle Scholar
[17]Sinnamon, G., ‘Embeddings of concave functions and duals of Lorentz spaces’, Publ. Mat. 46 (2002), 489–515.CrossRefGoogle Scholar
[18]Sinnamon, G., ‘Transferring monotonicity in weighted norm inequalities’, Collect. Math. 54 (2003), 181–216.Google Scholar
[19]Sinnamon, G. and Stepanov, V.D., ‘The weighted Hardy inequality: new proofs and the case p = 1’, J. London Math. Soc. 54 (1996), 89–101.CrossRefGoogle Scholar
[20]Stepanov, V.D., ‘The weighted Hardy's inequality for nonincreasing functions’, Thans. Amer. Math. Soc. 338 (1993), 173–186.Google Scholar
[21]Stepanov, V.D., ‘Integral operators on the cone of monotone functions’, J. London Math. Soc. 48 (1993), 465–487.CrossRefGoogle Scholar