Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-28T19:51:12.766Z Has data issue: false hasContentIssue false
  • English
  • Français

DIAMETER OF COMMUTING GRAPHS OF SYMPLECTIC ALGEBRAS

Part of: Graph theory Basic linear algebra

Published online by Cambridge University Press:  04 June 2019

XIANYA GENG Open the ORCID record for XIANYA GENG [Opens in a new window] ,
LITING FAN Open the ORCID record for LITING FAN [Opens in a new window]  and
XIAOBIN MA Open the ORCID record for XIAOBIN MA [Opens in a new window]
XIANYA GENG*
Affiliation:
School of Mathematics and Big Data, Anhui University of Science and Technology, Huainan, PR China email gengxianya@sina.com
LITING FAN
Affiliation:
School of Mathematics and Big Data, Anhui University of Science and Technology, Huainan, PR China email 1275371706@qq.com
XIAOBIN MA
Affiliation:
School of Mathematics and Big Data, Anhui University of Science and Technology, Huainan, PR China email xiaobintiandi@163.com
*
✉gengxianya@sina.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 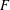$F$ be an algebraically closed field of characteristic 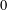$0$ and let 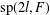$\operatorname{sp}(2l,F)$ be the rank 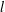$l$ symplectic algebra of all 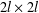$2l\times 2l$ matrices 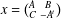$x=\big(\!\begin{smallmatrix}A & B\\ C & -A^{t}\end{smallmatrix}\!\big)$ over 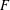$F$, where 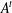$A^{t}$ is the transpose of 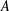$A$ and 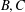$B,C$ are symmetric matrices of order 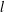$l$. The commuting graph 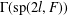$\unicode[STIX]{x1D6E4}(\operatorname{sp}(2l,F))$ of 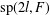$\operatorname{sp}(2l,F)$ is a graph whose vertex set consists of all nonzero elements in 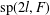$\operatorname{sp}(2l,F)$ and two distinct vertices $x$ and 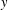$y$ are adjacent if and only if 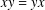$xy=yx$. We prove that the diameter of 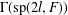$\unicode[STIX]{x1D6E4}(\operatorname{sp}(2l,F))$ is 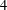$4$ when 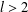$l>2$.

Keywords

commuting graphsdiameterLie algebras

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Secondary: 15A27: Commutativity 15A30: Algebraic systems of matrices
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 419 - 427
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Financially supported by the National Natural Science Foundation of China (Grant Nos. 11671164, 11271149).

References

Abdollahi, A., ‘Commuting graphs of full matrix rings over finite fields’, Linear Algebra Appl. 428 (2008), 2947–2954.Google Scholar
Abdollahi, A. and Shahverdi, H., ‘Characterization of the alternating group by its non-commuting graph’, J. Algebra 357 (2012), 203–207.Google Scholar
Akbari, S., Ghandehari, M., Hadian, M. and Mohammadian, A., ‘On commuting graphs of semisimple rings’, Linear Algebra Appl. 390 (2004), 345–355.Google Scholar
Akbari, S., Mohammadian, A., Radjavi, H. and Raja, P., ‘On the diameters of commuting graphs’, Linear Algebra Appl. 418 (2006), 161–176.Google Scholar
Akbari, S. and Raja, P., ‘Commuting graphs of some subsets in simple rings’, Linear Algebra Appl. 416 (2006), 1038–1047.Google Scholar
Carter, R. W., Simple Groups of Lie Type (Wiley Interscience, New York, 1972).Google Scholar
Dolžan, D., Bukovšek, D. K. and Oblak, P., ‘Diameters of commuting graphs of matrices over semirings’, Semigroup Forum 84 (2012), 365–373.Google Scholar
Dolžan, D. and Oblak, P., ‘Commuting graph of matrices over semirings’, Linear Algebra Appl. 435 (2011), 1657–1665.Google Scholar
Giudici, M. and Pope, A., ‘The diameters of commuting graphs of linear groups and matrix rings over the integers modulo m ’, Australas J. Combin. 48 (2010), 221–230.Google Scholar
Humphreys, J. E., Introduction to Lie Algebras and Representation Theory (Springer, New York, 1972).Google Scholar
Jacobson, N., Lie Algebras (Interscience Publishers, New York, 1962).Google Scholar
Miguel, C., ‘A note on a conjecture about commuting graphs’, Linear Algebra Appl. 438 (2013), 4750–4756.Google Scholar