Hostname: page-component-cc8bf7c57-l9twb Total loading time: 0 Render date: 2024-12-11T00:34:30.575Z Has data issue: false hasContentIssue false
  • English
  • Français

ELLIPTIC CURVES ARISING FROM BRAHMAGUPTA QUADRILATERALS

Part of: Curves

Published online by Cambridge University Press:  10 April 2014

FARZALI IZADI ,
FOAD KHOSHNAM ,
DUSTIN MOODY  and
ARMAN SHAMSI ZARGAR
FARZALI IZADI
Affiliation:
Department of Mathematics, Azarbaijan Shahid Madani University, Tabriz 53751-71379, Iran email farzali.izadi@azaruniv.edu
FOAD KHOSHNAM
Affiliation:
Department of Mathematics, Azarbaijan Shahid Madani University, Tabriz 53751-71379, Iran email khoshnam@azaruniv.edu
DUSTIN MOODY*
Affiliation:
Computer Security Division, National Institute of Standards and Technology, 100 Bureau Drive, Gaithersburg, MD 20899-8930, USA email dustin.moody@nist.gov
ARMAN SHAMSI  ZARGAR
Affiliation:
Department of Mathematics, Azarbaijan Shahid Madani University, Tabriz 53751-71379, Iran email shzargar.arman@azaruniv.edu
*
✉dustin.moody@nist.gov
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Brahmagupta quadrilateral is a cyclic quadrilateral whose sides, diagonals and area are all integer values. In this article, we characterise the notions of Brahmagupta, introduced by K. R. S. Sastry [‘Brahmagupta quadrilaterals’, Forum Geom. 2 (2002), 167–173], by means of elliptic curves. Motivated by these characterisations, we use Brahmagupta quadrilaterals to construct infinite families of elliptic curves with torsion group 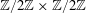$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$ having ranks (at least) four, five and six. Furthermore, by specialising we give examples from these families of specific curves with rank nine.

Keywords

Brahmagupta quadrilateralelliptic curveHeron trianglerank

MSC classification

Secondary: 14H52: Elliptic curves
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 1 , August 2014 , pp. 47 - 56
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aguirre, J., Dujella, A. and Peral, J. C., ‘On the rank of elliptic curves coming from rational Diophantine triples’, Rocky Mountain J. Math. 42 (2012), 1759–1776.Google Scholar
Alsina, C. and Nelsen, R. B., ‘On the diagonals of a cyclic quadrilateral’, Forum Geom. 7 (2007), 147–149.Google Scholar
Buchholz, R. H. and Macdougall, J. A., ‘Heron quadrilaterals with sides in arithmetic or geometric progression’, Bull. Aust. Math. Soc. 59 (1999), 263–269.Google Scholar
Cremona, J., http://maths.nottingham.ac.uk/personal/jec/ftp/progs/.Google Scholar
Daia, L., ‘On a conjecture’, Gaz. Mat. 89 (1984), 276–279 (in Romanian).Google Scholar
Dickson, L. E., History of the Theory of Numbers II (Chelsea, New York, 1971).Google Scholar
Dujella, A., ‘Diophantine triples and construction of high-rank elliptic curves over ℚ with three nontrivial 2-torsion points’, Rocky Mountain J. Math. 30 (2000), 157–164.CrossRefGoogle Scholar
Dujella, A., ‘Irregular Diophantine m-tuples and elliptic curves of high rank’, Proc. Japan Acad. Ser. A Math. Sci. 76 (2000), 66–67.Google Scholar
Dujella, A., http://web.math.pmf.unizg.hr/ duje/tors/tors.html.Google Scholar
Dujella, A., http://web.math.pmf.unizg.hr/ duje/tors/generic.html.Google Scholar
Dujella, A. and Peral, J. C., ‘Elliptic curves coming from Heron triangles’, Rocky Mountain J. Math., to appear.Google Scholar
Elkies, N. D., ‘Three lectures on elliptic surfaces and curves of high rank’, Preprint, 2007, arXiv:0709.2908.Google Scholar
Gupta, R. C., ‘Parameśvara’s rule for the circumradius of a cyclic quadrilateral’, Historia Math. 4 (1977), 67–74.Google Scholar
Ismailescu, D. and Vojdany, A., ‘Class preserving dissections of convex quadrilatrals’, Forum Geom. 9 (2009), 195–211.Google Scholar
Izadi, F., Khoshnam, F. and Nabardi, K., ‘A new family of elliptic curves with positive ranks arising from the Heron triangles’, Preprint, 2010, arXiv:1012.5835.Google Scholar
Mestre, J. -F., ‘Construction de courbes elliptiques sur ℚ de rang ≥ 12’, C. R. Acad. Sci. Paris Ser. I 295 (1982), 643–644.Google Scholar
Nagao, K., ‘An example of elliptic curve over ℚ with rank ≥ 20’, Proc. Japan Acad. Ser. A Math. Sci. 69 (1993), 291–293.CrossRefGoogle Scholar
SAGE software, Version 4.3.5, http://sagemath.org.Google Scholar
Sastry, K. R. S., ‘Brahmagupta quadrilaterals’, Forum Geom. 2 (2002), 167–173.Google Scholar
Silverman, J. H., Advanced Topics in the Arithmetic of Elliptic Curves (Springer, New York, 1994).Google Scholar