Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T21:41:41.024Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE TRIFACTORISED GROUPS AND $\unicode[STIX]{x1D70B}$-DECOMPOSABILITY

Part of: Representation theory of groups

Published online by Cambridge University Press:  31 January 2018

L. S. KAZARIN ,
A. MARTÍNEZ-PASTOR Open the ORCID record for A. MARTÍNEZ-PASTOR [Opens in a new window]  and
M. D. PÉREZ-RAMOS Open the ORCID record for M. D. PÉREZ-RAMOS [Opens in a new window]
L. S. KAZARIN
Affiliation:
Department of Mathematics, Yaroslavl P. Demidov State University, Sovetskaya Str. 14, 150003 Yaroslavl, Russia email Kazarin@uniyar.ac.ru
A. MARTÍNEZ-PASTOR*
Affiliation:
Instituto Universitario de Matemática Pura y Aplicada IUMPA-UPV, Universitat Politècnica de València, Camino de Vera, s/n, 46022 València, Spain email anamarti@mat.upv.es
M. D. PÉREZ-RAMOS
Affiliation:
Departament de Matemàtiques, Universitat de València, C/ Doctor Moliner 50, 46100 Burjassot (València), Spain email Dolores.Perez@uv.es
*
✉anamarti@mat.upv.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We derive some structural properties of a trifactorised finite group 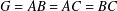$G=AB=AC=BC$, where 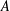$A$, 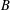$B$, and 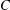$C$ are subgroups of 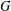$G$, provided that 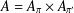$A=A_{\unicode[STIX]{x1D70B}}\times A_{\unicode[STIX]{x1D70B}^{\prime }}$ and $B=B_{\unicode[STIX]{x1D70B}}\times B_{\unicode[STIX]{x1D70B}^{\prime }}$ are $\unicode[STIX]{x1D70B}$-decomposable groups, for a set of primes $\unicode[STIX]{x1D70B}$.

Keywords

finite groupsproducts of subgroups𝜋-decomposable groups𝜋-structure

MSC classification

Primary: 20D40: Products of subgroups
Secondary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 218 - 228
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by Project VIP-008 of Yaroslavl P. Demidov State University and by a research grant from the Universitat de València as research visitor (Programa Propi d’Ajudes a la Investigació de la Universitat de València, Subprograma d’Atracció de Talent de VLC-Campus, Estades d’investigadors convidats (2017)). The second and third authors were supported by Proyecto MTM2014-54707-C3-1-P, Ministerio de Economía y Competitividad, Spain.

References

Amberg, B., Franciosi, S. and de Giovanni, F., Products of Groups (Clarendon Press, Oxford, 1992).Google Scholar
Arad, Z. and Fisman, E., ‘On finite factorizable groups’, J. Algebra 86 (1984), 522–548.Google Scholar
Ballester-Bolinches, A., Martínez-Pastor, A. and Pedraza-Aguilera, M. C., ‘Finite trifactorized groups and formations’, J. Algebra 226 (2000), 990–1000.Google Scholar
Ballester-Bolinches, A., Martínez-Pastor, A. and Pérez-Ramos, M. D., ‘Nilpotent-like Fitting formations of finite soluble groups’, Bull. Aust. Math. Soc. 62 (2000), 427–433.Google Scholar
Ballester-Bolinches, A., Martínez-Pastor, A., Pedraza-Aguilera, M. C. and Pérez-Ramos, M. D., ‘On nilpotent-like Fitting formations’, in: Groups St Andrews 2001 in Oxford, Vol. I, London Mathematical Society Lecture Note Series, 304 (Cambridge University Press, Cambridge, 2003), 31–38.Google Scholar
Doerk, K. and Hawkes, T., Finite Soluble Groups (Walter de Gruyter, Berlin, 1992).Google Scholar
Kazarin, L. S., ‘Factorizations of finite groups by solvable subgroups’, Ukr. Mat. J. 43(7) (1991), 883–886.Google Scholar
Kazarin, L. S., Martínez-Pastor, A. and Pérez-Ramos, M. D., ‘On the product of a 𝜋-group and a 𝜋-decomposable group’, J. Algebra 315 (2007), 640–653.Google Scholar
Kazarin, L. S., Martínez-Pastor, A. and Pérez-Ramos, M. D., ‘On the product of two 𝜋-decomposable soluble groups’, Publ. Mat. 53 (2009), 439–456.Google Scholar
Kazarin, L. S., Martínez-Pastor, A. and Pérez-Ramos, M. D., ‘Extending the Kegel–Wielandt theorem through 𝜋-decomposable groups’, in: Groups St Andrews 2009 in Bath, Vol. 2, London Mathematical Society Lecture Note Series, 388 (Cambridge University Press, Cambridge, 2011), 415–423.Google Scholar
Kazarin, L. S., Martínez-Pastor, A. and Pérez-Ramos, M. D., ‘A reduction theorem for a conjecture on products of two 𝜋-decomposable groups’, J. Algebra 379 (2013), 301–313.Google Scholar
Kazarin, L. S., Martínez-Pastor, A. and Pérez-Ramos, M. D., ‘On the product of two 𝜋-decomposable groups’, Rev. Mat. Iberoam. 31 (2015), 51–68.Google Scholar
Kegel, O. H., ‘Zur Struktur mehrfach faktorisierter endlicher Gruppen’, Math. Z. 87 (1965), 42–48.CrossRefGoogle Scholar
Pennington, E., ‘Trifactorisable groups’, Bull. Aust. Math. Soc. 8 (1973), 461–469.Google Scholar
Revin, D. O. and Vdovin, E. P., ‘Hall subgroups in finite groups’, in: Ischia Group Theory 2004, Contemporary Mathematics, 402 (American Mathematical Society, Providence, RI, 2006), 229–263.CrossRefGoogle Scholar
Robinson, D. J., A Course in the Theory of Groups (Springer, New York, 1982).Google Scholar