A group 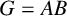$G=AB$ is the weakly mutually permutable product of the subgroups A and B, if A permutes with every subgroup of B containing 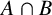$A \cap B$ and B permutes with every subgroup of A containing 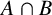$A \cap B$. Weakly mutually permutable products were introduced by the first, second and fourth authors [‘Generalised mutually permutable products and saturated formations’, J. Algebra 595 (2022), 434–443] who showed that if 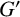$G'$ is nilpotent, A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, then 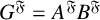$G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}} $, where 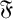$ \mathfrak {F} $ is a saturated formation containing 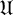$ \mathfrak {U} $, the class of supersoluble groups. In this article we prove results on weakly mutually permutable products concerning 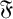$ \mathfrak {F} $-residuals, 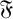$ \mathfrak {F} $-projectors and 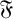$\mathfrak {F}$-normalisers. As an application of some of our arguments, we unify some results on weakly mutually 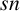$sn$-products.