Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-30T14:51:08.719Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERALISED WEIGHTED COMPOSITION OPERATORS ON BERGMAN SPACES INDUCED BY DOUBLING WEIGHTS

Part of: Spaces and algebras of analytic functions Special classes of linear operators

Published online by Cambridge University Press:  08 January 2021

BIN LIU Open the ORCID record for BIN LIU [Opens in a new window]
BIN LIU*
Affiliation:
University of Eastern Finland, Joensuu P.O. Box 111, 80101, Finland
*
e-mail: binl@uef.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterise bounded and compact generalised weighted composition operators acting from the weighted Bergman space $A^p_\omega $, where $0<p<\infty $ and 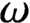$\omega $ belongs to the class 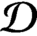$\mathcal {D}$ of radial weights satisfying a two-sided doubling condition, to a Lebesgue space 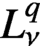$L^q_\nu $. On the way, we establish a new embedding theorem on weighted Bergman spaces $A^p_\omega $ which generalises the well-known characterisation of the boundedness of the differentiation operator 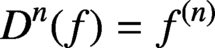$D^n(f)=f^{(n)}$ from the classical weighted Bergman space 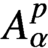$A^p_\alpha $ to the Lebesgue space $L^q_\mu $, induced by a positive Borel measure 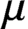$\mu $, to the setting of doubling weights.

Keywords

Carleson measuredoubling weightsweighted Bergman spaceweighted composition operators

MSC classification

Primary: 47B33: Composition operators
Secondary: 30H20: Bergman spaces, Fock spaces

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 141 - 153
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research was supported in part by the China Scholarship Council, No. 201706330108.

References

Cowen, C. C. and MacCluer, B. D., Composition Operators on Spaces of Analytic Functions, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1995).Google Scholar
Čučković, Ž. and Zhao, R., ‘Weighted composition operators between different weighted Bergman spaces and different Hardy spaces’, Illinois J. Math. 51(2) (2007), 479–498.CrossRefGoogle Scholar
Goebeler, T. E. Jr, ‘Composition operators acting between Hardy spaces’, Integral Equations Operator Theory 41(4) (2001), 389–395.CrossRefGoogle Scholar
Halmos, P. R., Measure Theory (Springer, New York, 1974).Google Scholar
Hibschweiler, R. and Portnoy, N., ‘Composition followed by differentiation between Bergman and Hardy spaces’, Rocky Mountain J. Math. 35 (2005), 843–855.CrossRefGoogle Scholar
Li, S. and Stević, S., ‘Composition followed by differentiation between Bloch type spaces’, J. Comput. Anal. Appl. 9 (2017), 195–205.Google Scholar
Liu, B. and Rättyä, J., ‘Compact differences of weighted composition operators’, Collectanea Mathematica, to appear.Google Scholar
Liu, B., Rättyä, J. and Wu, F., ‘Compact differences of composition operators on Bergman spaces induced by doubling weights’, Preprint, 2020, arXiv:2007.04907.Google Scholar
Luecking, D. H., ‘Forward and reverse inequalities for functions in Bergman spaces and their derivatives’, Amer. J. Math. 107 (1985), 85–111.CrossRefGoogle Scholar
Luecking, D. H., ‘Embedding theorems for spaces of analytic functions via Khinchine’s inequality’, Michigan Math. J. 40(2) (1993), 333–358.CrossRefGoogle Scholar
Peláez, J. A., ‘Small weighted Bergman spaces’, Proc. Summer School in Complex and Harmonic Analysis and Related Topics, Publ. Univ. East. Finl. Rep. Stud. For. Nat. Sci., vol. 22 (Univ. East. Finl., Joensuu, 2016), 29–98.Google Scholar
Peláez, J. A. and Rättyä, J., ‘Weighted Bergman spaces induced by rapidly increasing weights’, Mem. Amer. Math. Soc. 227(1066) (2014), 124 pages.Google Scholar
Peláez, J. A. and Rättyä, J., ‘Embedding theorems for Bergman spaces via harmonic analysis’, Math. Ann. 362(1–2) (2015), 205–239.CrossRefGoogle Scholar
Peláez, J. A. and Rättyä, J., ‘Bergman projection induced by radial weight’, Preprint, 2019, arXiv:1902.09837.Google Scholar
Peláez, J. A., Rättyä, J. and Sierra, K., ‘Berezin transform and Toeplitz operators on Bergman spaces induced by regular weights’, J. Geom. Anal. 28(1) (2018), 656–687.CrossRefGoogle Scholar
Peláez, J. A., Rättyä, J. and Sierra, K., ‘Atomic decomposition and Carleson measures for weighted mixed norm spaces’, J. Geom. Anal. (2019), 33 pages. Published online (18 October 2019).Google Scholar
Shapiro, J. H., ‘The essential norm of a composition operator’, Ann. of Math. (2) 125(2) (1987), 375–404.CrossRefGoogle Scholar
Shapiro, J. H., Composition Operators and Classical Function Theory, Universitext: Tracts in Mathematics (Springer, New York, 1993).CrossRefGoogle Scholar
Smith, W., ‘Composition operators between Bergman and Hardy spaces’, Trans. Amer. Math. Soc. 348(6) (1996), 2331–2348.CrossRefGoogle Scholar
Zhu, K., Operator Theory in Function Spaces (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar
Zhu, X., ‘Products of differentiation, composition and multiplication from Bergman type spaces to Bers type space’, Integral Transforms Spec. Funct. 18 (2007), 223–231.CrossRefGoogle Scholar
Zhu, X., ‘Generalized weighted composition operators on weighted Bergman spaces’, Numer. Funct. Anal. Optim. 30(7–8) (2008), 881–893.CrossRefGoogle Scholar