Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-23T21:02:05.140Z Has data issue: false hasContentIssue false
  • English
  • Français

GEOMETRIC AND FIXED POINT PROPERTIES IN PRODUCTS OF NORMED SPACES

Part of: Nonlinear operators and their properties Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  10 January 2019

M. VEENA SANGEETHA Open the ORCID record for M. VEENA SANGEETHA [Opens in a new window]
M. VEENA SANGEETHA*
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai 600 036, India email veena176@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given two (real) normed (linear) spaces 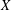$X$ and 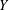$Y$, let 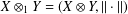$X\otimes _{1}Y=(X\otimes Y,\Vert \cdot \Vert )$, where 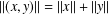$\Vert (x,y)\Vert =\Vert x\Vert +\Vert y\Vert$. It is known that 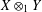$X\otimes _{1}Y$ is 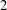$2$-UR if and only if both 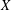$X$ and 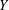$Y$ are UR (where we use UR as an abbreviation for uniformly rotund). We prove that if 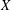$X$ is 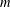$m$-dimensional and 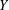$Y$ is 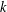$k$-UR, then 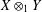$X\otimes _{1}Y$ is $(m+k)$-UR. In the other direction, we observe that if 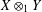$X\otimes _{1}Y$ is 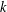$k$-UR, then both 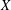$X$ and 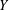$Y$ are 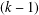$(k-1)$-UR. Given a monotone norm 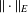$\Vert \cdot \Vert _{E}$ on 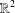$\mathbb{R}^{2}$, we let 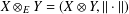$X\otimes _{E}Y=(X\otimes Y,\Vert \cdot \Vert )$ where 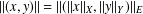$\Vert (x,y)\Vert =\Vert (\Vert x\Vert _{X},\Vert y\Vert _{Y})\Vert _{E}$. It is known that if 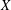$X$ is uniformly rotund in every direction, 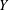$Y$ has the weak fixed point property for nonexpansive maps (WFPP) and 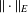$\Vert \cdot \Vert _{E}$ is strictly monotone, then 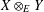$X\otimes _{E}Y$ has WFPP. Using the notion of 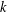$k$-uniform rotundity relative to every 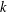$k$-dimensional subspace we show that this result holds with a weaker condition on 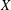$X$.

Keywords

relative k-uniform rotundityUREk spacesnonexpansive mapsweak fixed point propertyproducts of normed spacesmonotone norms

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 47H09: Contraction-type mappings, nonexpansive mappings, $A$-proper mappings, etc. 47H10: Fixed-point theorems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 2 , April 2019 , pp. 262 - 273
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

Some of the results in this article are part of the author’s PhD thesis written at the Indian Institute of Technology Madras, Chennai, India with the financial support of the Council of Scientific and Industrial Research, New Delhi, India.

References

Alspach, D. E., ‘A fixed point free nonexpansive map’, Proc. Amer. Math. Soc. 82(3) (1981), 423–424.Google Scholar
Amir, D. and Ziegler, Z., ‘Relative Chebyshev centers in normed linear spaces. II’, J. Approx. Theory 38(4) (1983), 293–311.Google Scholar
Casini, E., ‘Degree of convexity and product spaces’, Comment. Math. Univ. Carolin. 31(4) (1990), 637–641.Google Scholar
Clarkson, J. A., ‘Uniformly convex spaces’, Trans. Amer. Math. Soc. 40(3) (1936), 396–414.Google Scholar
Day, M. M., James, R. C. and Swaminathan, S., ‘Normed linear spaces that are uniformly convex in every direction’, Canad. J. Math. 23 (1971), 1051–1059.Google Scholar
Garkavi, A. L., ‘On the optimal net and best cross-section of a set in a normed space’, Izv. Akad. Nauk SSSR Ser. Mat. 26 (1962), 87–106.Google Scholar
Geremia, R. and Sullivan, F., ‘Multidimensional volumes and moduli of convexity in Banach spaces’, Ann. Mat. Pura Appl. (4) 127 (1981), 231–251.Google Scholar
Goebel, K., ‘On the structure of minimal invariant sets for nonexpansive mappings’, Ann. Univ. Mariae Curie-Skłodowska Sect. A 29 (1975), 73–77.Google Scholar
Goebel, K. and Kirk, W. A., Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics, 28 (Cambridge University Press, Cambridge, 1990).Google Scholar
Karlovitz, L. A., ‘Existence of fixed points of nonexpansive mappings in a space without normal structure’, Pacific J. Math. 66(1) (1976), 153–159.Google Scholar
Kirk, W. A., ‘A fixed point theorem for mappings which do not increase distances’, Amer. Math. Monthly 72 (1965), 1004–1006.Google Scholar
Kuczumow, T., Reich, S. and Schmidt, M., ‘A fixed point property of ℓ 1 -product spaces’, Proc. Amer. Math. Soc. 119(2) (1993), 457–463.Google Scholar
Lin, P. K., ‘ k-uniform rotundity is equivalent to k-uniform convexity’, J. Math. Anal. Appl. 132(2) (1988), 349–355.Google Scholar
Llorens-Fuster, E., ‘The fixed point property for renormings of ℓ 2 ’, Arab. J. Math. 1(4) (2012), 511–528.Google Scholar
Milman, V. D., ‘Geometric theory of Banach spaces. II. Geometry of the unit ball’, Uspekhi Mat. Nauk 26(6(162)) (1971), 73–149.Google Scholar
Sullivan, F., ‘A generalization of uniformly rotund Banach spaces’, Canad. J. Math. 31(3) (1979), 628–636.Google Scholar
Tan, K. K. and Xu, H. K., ‘On fixed point theorems of nonexpansive mappings in product spaces’, Proc. Amer. Math. Soc. 113(4) (1991), 983–989.Google Scholar
Veena Sangeetha, M., ‘On relative $k$ -uniform rotundity, normal structure and fixed point property for nonexpansive maps’, Preprint.Google Scholar
Veena Sangeetha, M. and Veeramani, P., ‘Uniform rotundity with respect to finite-dimensional subspaces’, J. Convex Anal. 25(4) (2018), 1223–1252.Google Scholar
Wiśnicki, A., ‘On the fixed points of nonexpansive mappings in direct sums of Banach spaces’, Studia Math. 207(1) (2011), 75–84.Google Scholar