Hostname: page-component-7dd5485656-bt4hw Total loading time: 0 Render date: 2025-10-31T08:16:24.407Z Has data issue: false hasContentIssue false
  • English
  • Français

MIN-PHASE-ISOMETRIES IN STRICTLY CONVEX NORMED SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  22 March 2023

DONGNI TAN Open the ORCID record for DONGNI TAN [Opens in a new window]  and
FAN ZHANG Open the ORCID record for FAN ZHANG [Opens in a new window]
DONGNI TAN*
Affiliation:
School of Computer Science and Engineering, Tianjin University of Technology, Tianjin 300384, PR China
FAN ZHANG
Affiliation:
Department of Mathematics, Tianjin University of Technology, Tianjin 300384, PR China e-mail: zhangfan795@163.com
*
e-mail: tandongni0608@sina.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that X and Y are two real normed spaces. A map 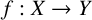$f:X\rightarrow Y$ is called a min-phase-isometry if it satisfies

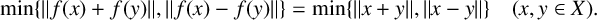$$ \begin{align*} \min\{\|f(x)+f(y)\|,\|f(x)-f(y)\|\}=\min\{\|x+y\|,\|x-y\|\} \quad (x,y\in X). \end{align*} $$

We present properties of min-phase-isometries in the case that Y is strictly convex and show that if a min-phase-isometry f (not necessarily surjective) fixes the origin, then it is phase-equivalent to a linear isometry, that is, 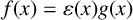$f(x)=\varepsilon (x)g(x)$ for 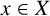$x\in X$, where 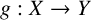$g:X\rightarrow Y$ is a linear isometry and 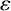$\varepsilon $ is a map from X to 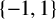$\{-1,1\}$.

Keywords

Wigner’s theoremstrictly convexmin-phase-isometryphase-equivalent

MSC classification

Primary: 46B04: Isometric theory of Banach spaces
Secondary: 46B20: Geometry and structure of normed linear spaces

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 1 , February 2024 , pp. 152 - 160
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author is supported by the Natural Science Foundation of China (Grant No. 12271402) and the Natural Science Foundation of Tianjin City (Grant No. 22JCYBJC00420).

References

Bunk, O., Diaz, A., Pfeiffer, F., David, C., Schmitt, B., Satapathy, D. K. and van der Veen, J. F., ‘Diffractive imaging for periodic samples: retrieving one-dimensional concentration profiles across microfluidic channels’, Acta Crystallogr. A 63(4) (2007), 306–314.CrossRefGoogle ScholarPubMed
Chevalier, G., ‘Wigner’s theorem and its generalizations’, in: Handbook of Quantum Logic and Quantum Structures (eds. Engesser, K., Gabbay, D. M. and Lehmann, D.) (Elsevier, Amsterdam, 2007), 429–475.CrossRefGoogle Scholar
Faure, C. A., ‘An elementary proof of the fundamental theorem of projective geometry’, Geom. Dedicata 90 (2002), 145–151.CrossRefGoogle Scholar
Fienup, C. and Dainty, J., ‘Phase retrieval and image reconstruction for astronomy’, in: Image Recovery: Theory and Application (ed. Stark, H.) (Academic Press, Orlando, FL, 1987), 231–275.Google Scholar
Gehér, G. P., ‘An elementary proof for the non-bijective version of Wigner’s theorem’, Phys. Lett. A 378 (2014), 2054–2057.CrossRefGoogle Scholar
Győry, M., ‘A new proof of Wigner’s theorem’, Rep. Math. Phys. 54 (2004), 159–167.CrossRefGoogle Scholar
Huang, X. and Tan, D., ‘Wigner’s theorem in atomic ${L}_p$ -spaces $\left(p>0\right)$ ’, Publ. Math. Debrecen 92(3–4) (2018), 411–418.CrossRefGoogle Scholar
Huang, X. and Tan, D., ‘Phase-isometries on real normed spaces’, J. Math. Anal. Appl. 488(1) (2020), Article no. 124058.Google Scholar
Huang, X. and Tan, D., ‘The Wigner property for CL-spaces and finite-dimensional polyhedral Banach spaces’, Proc. Edinb. Math. Soc. (2) 64(2), (2021), 183–199.Google Scholar
Huang, X. and Tan, D., ‘Min-phase-isometries and Wigner’s theorem on real normed spaces’, Results Math. 77 (2022), 152.CrossRefGoogle Scholar
Ilišević, D., Omladič, M. and Turnšek, A., ‘On Wigner’s theorem in strictly convex normed spaces’, Publ. Math. Debrecen 97 (2020), 393–401.CrossRefGoogle Scholar
Ilišević, D., Omladič, M. and Turnšek, A., ‘Phase-isometries between normed spaces’, Linear Algebra Appl. 612 (2021), 99–111.CrossRefGoogle Scholar
Jaming, P.. ‘Phase retrieval techniques for radar ambiguity problems’, J. Fourier Anal. Appl. 5(4) (1999), 309–329.CrossRefGoogle Scholar
Maksa, G. and Páles, Z., ‘Wigner’s theorem revisited’, Publ. Math. Debrecen 81 (2012), 243–249.CrossRefGoogle Scholar
Rabiner, L. and Juang, B. H., Fundamentals of Speech Recognition (Prentice-Hall, Upper Saddle River, NJ, 1993).Google Scholar
Sharma, C. S. and Almeida, D. L., ‘A direct proof of Wigner’s theorem on maps which preserve transition probabilities between pure states of quantum systems’, Ann. Phys. 197(2) (1990), 300–309.CrossRefGoogle Scholar
Turnšek, A., ‘A variant of Wigner’s functional equation’, Aequationes Math. 89(4) (2015), 1–8.CrossRefGoogle Scholar
Wang, R. and Bugajewski, D., ‘On normed spaces with the Wigner property’, Ann. Funct. Anal. 11 (2020), 523–539.CrossRefGoogle Scholar