Hostname: page-component-7bb8b95d7b-qxsvm Total loading time: 0 Render date: 2024-09-18T07:59:33.353Z Has data issue: false hasContentIssue false
  • English
  • Français

The modular counterparts of Cayley's hyperdeterminants

Published online by Cambridge University Press:  17 April 2009

David G. Glynn
David G. Glynn
Affiliation:
Te Tari TatauTe Whare Wānanga o WaitahaP.B. 4800ŌtautahiAotearoa (New Zealand) e-mail: D.Glynn@math.canterbury.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H be a hypersurface of degree m in PG(n, q), q = ph, p prime.

(1) If m < n + 1, H has 1 (mod p) points.

(2) If m = n + 1, H has 1 (mod p) points ⇔ Hp−1 has no term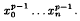

We show some applications, including the generalised Hasse invariant for hypersurfaces of degree n + 1 in PG(n, F), various porperties of finite projective spaces, and in particular a p-modular invariant detp of any (n + 1)r+2 = (n + 1)×…×(n + 1) array on hypercube A over a field characteristic p. This invariant is multiplicative in that detp(AB) = detp(B), whenever the product (or convolution of the two arrays A and B is defined, and both arrays are not 1-dimensional vectors. (If A is (n + 1)r+2 and B is (n + 1)s+2, then AB is (n + 1)r+s+2.) The geometrical meaning of the invariant is that over finite fields of characteristic p the number of projections of A from r + 1 points in any given r + 1 directions of the array to a non-zero point in the final direction is 0 (mod p). Equivalently, the number of projections of A from r points in any given r directions to a non-singular (n + 1)2 matrix is 0 (mod p). Historical aspects of invariant theory and connections with Cayley's hyperdeterminant Det for characteristic 0 fields are mentioned.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 57 , Issue 3 , June 1998 , pp. 479 - 492
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Assmus, E. and Key, J.D., Designs and their Codes (Cambridge University Press, Cambridge, 1993).Google Scholar
[2]Cayley, A., ‘On the theory of linear transformations’, Cambr. Math. J. 4 (1845), 193–209.Google Scholar
[3]Cayley, A., ‘On linear transformations’, Cambr. and Dublin Math. J. 1 (1846), 104–122.Google Scholar
[4]Cayley, A., ‘Note sur un système de certaines formules’, J. Reine Angew. Math. 39 (1850), 14–15.Google Scholar
[5]Cayley, A., Collected Mathematical Papers 1 (Cambridge University Press, Cambridge, 1889).Google Scholar
[6]Coolidge, J.L., A history of geometrical methods (Oxford University Press, Oxford, 1940).Google Scholar
[7]Dickson, L.E., History of the theory of numbers, III, Chapter 19 (Chelsea Publishing Co., New York, 1966). (See also Vol I, pp.231–233, with a report on A. Hurwitz’ work).Google Scholar
[8]Gauß, C.F., Disquisitiones arithmeticae, 1801.CrossRefGoogle Scholar
[9]Glynn, D.G., ‘On cubic curves in projective planes of characteristic two’, Australas. J. Combin. 17 (1998), 1–20.Google Scholar
[10]Glynn, D.G. and Hirschfeld, J.W.P., ‘On the classification of geometric codes by polynomial functions’, Des. Codes Cryptogr. 6 (1995), 189–204.CrossRefGoogle Scholar
[11]Gelfand, I.M., Kapranov, M.M. and Zelevinsky, A.V., Discriminants, resultants and multidimensional determinants (Birkhäuser, Boston, Basel, Berlin, 1994).CrossRefGoogle Scholar
[12]Hartshorne, R., Algebraic geometry (Springer, Berlin, Heidelberg, New York, 1983), pp. 332–340.Google Scholar
[13]Hirschfeld, J.W.P., Projective geometry over a finite field (Oxford University Press, Oxford, 1979).Google Scholar
[14]Schläfli, L., ‘Über die Resultante eines Systemes mehrerer algebraischen Gleichungen’, Denkschr. der Kaiserlicher Akad. der Wiss., math-naturwiss. Klasse 4 (1852).Google Scholar
[15]Schläfli, L., Gesammelte Abhandlungen 2 (Birkhäuser Verlag, Basel, 1953).Google Scholar