Hostname: page-component-7dd5485656-s6l46 Total loading time: 0 Render date: 2025-10-28T01:17:41.638Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING PRIMITIVE PYTHAGOREAN TRIPLES

Part of: Diophantine equations

Published online by Cambridge University Press:  26 September 2016

MOU-JIE DENG  and
DONG-MING HUANG
MOU-JIE DENG*
Affiliation:
Department of Applied Mathematics, Hainan University, Haikon, Hainan 570228, PR China email Moujie_Deng@163.com
DONG-MING HUANG
Affiliation:
Department of Applied Mathematics, Hainan University, Haikon, Hainan 570228, PR China email Huangdm35@126.com
*
✉ Moujie_Deng@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 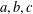$a,b,c$ be a primitive Pythagorean triple and set 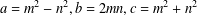$a=m^{2}-n^{2},b=2mn,c=m^{2}+n^{2}$ , where 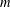$m$ and $n$ are positive integers with 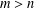$m>n$ , 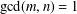$\text{gcd}(m,n)=1$ and 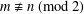$m\not \equiv n~(\text{mod}~2)$ . In 1956, Jeśmanowicz conjectured that the only positive integer solution to the Diophantine equation 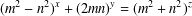$(m^{2}-n^{2})^{x}+(2mn)^{y}=(m^{2}+n^{2})^{z}$ is 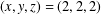$(x,y,z)=(2,2,2)$ . We use biquadratic character theory to investigate the case with 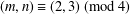$(m,n)\equiv (2,3)~(\text{mod}~4)$ . We show that Jeśmanowicz’ conjecture is true in this case if 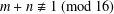$m+n\not \equiv 1~(\text{mod}~16)$ or 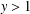$y>1$ . Finally, using these results together with Laurent’s refinement of Baker’s theorem, we show that Jeśmanowicz’ conjecture is true if 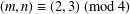$(m,n)\equiv (2,3)~(\text{mod}~4)$ and 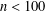$n<100$ .

Keywords

exponential Diophantine equationsPythagorean triplesJeśmanowicz’ conjecture

MSC classification

Primary: 11D61: Exponential equations

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 1 , February 2017 , pp. 5 - 13
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Cao, Z. F., ‘A note on the Diophantine equation a x + b y = c z ’, Acta Arith. 91 (1999), 85–93.CrossRefGoogle Scholar
Deḿjanenko, V. A., ‘On Jeśmanowicz’ problem for Pythagorean numbers’, Izv. Vyssh. Uchebn. Zaved. Mat. 48 (1965), 52–56 (in Russian).Google Scholar
Deng, M. J., ‘A note on the Diophantine equation (a 2 - b 2) x + (2ab) y = (a 2 + b 2) z ’, J. Nat. Sci. Heilongjiang Univ. 19 (2002), 8–10 (in Chinese).Google Scholar
Deng, M. J. and Cohen, G. L., ‘A note on a conjecture of Jeśmanowicz’, Colloq. Math. 86 (2000), 25–30.Google Scholar
Guo, Y. D. and Le, M. H., ‘A note on Jeśmanowicz’ conjecture concerning Pythagorean numbers’, Comment. Math. Univ. St. Pauli 44 (1995), 225–228.Google Scholar
Jeśmanowicz, L., ‘Several remarks on Pythagorean numbers’, Wiadom. Mat. 1 (1955–1956), 196–202 (in Polish).Google Scholar
Laurent, M., ‘Linear forms in two logarithms and interpolation determinants II’, Acta Arith. 133 (2008), 325–348.CrossRefGoogle Scholar
Le, M., ‘A note on Jeśmanowicz’ conjecture’, Colloq. Math. 69 (1995), 47–51.Google Scholar
Lu, W. T., ‘On the Pythagorean numbers 4n 2 - 1, 4n and 4n 2 + 1’, Acta Sci. Natur. Univ. Szechuan 2 (1959), 39–42 (in Chinese).Google Scholar
Miyazaki, T., ‘Generalizations of classical results on Jeśmanowicz’ conjecture concerning Pythagorean triples’, J. Number Theory 133 (2013), 583–595.CrossRefGoogle Scholar
Miyazaki, T. and Terai, N., ‘On Jeśmanowicz’ conjecture concerning primitive Pythagorean triples II’, Acta Math. Hungar. 147 (2015), 286–293.CrossRefGoogle Scholar
Miyazaki, T., Yuan, P. Z. and Wu, D. Y., ‘Generalizations of classical results on Jeśmanowicz’ conjecture concerning Pythagorean triples II’, J. Number Theory 141 (2014), 184–201.Google Scholar
Pan, C. D. and Pan, C. B., Algebraic Number Theory (Shandong University Press, Jinan, 2001), (in Chinese).Google Scholar
Sierpiński, W., ‘On the equation 3 x + 4 y = 5 z ’, Wiadom. Mat. 1 (1955–1956), 194–195 (in Polish).Google Scholar
Takakuwa, K., ‘A remark on Jeśmanowicz’ conjecture’, Proc. Japan Acad. Ser. A Math. Sci. 72 (1996), 109–110.Google Scholar
Terai, N., ‘On Jeśmanowicz’ conjecture concerning primitive Pythagorean triples’, J. Number Theory 141 (2014), 316–323.Google Scholar