Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-30T08:41:38.563Z Has data issue: false hasContentIssue false
  • English
  • Français

ON p-SOLVABILITY AND AVERAGE CHARACTER DEGREE IN A FINITE GROUP

Part of: Representation theory of groups

Published online by Cambridge University Press:  27 July 2023

ESMAEEL ESKANDARI Open the ORCID record for ESMAEEL ESKANDARI [Opens in a new window]  and
NEDA AHANJIDEH Open the ORCID record for NEDA AHANJIDEH [Opens in a new window]
ESMAEEL ESKANDARI
Affiliation:
Department of Pure Mathematics, Faculty of Mathematical Sciences, Shahrekord University, P.O. Box 115, Shahrekord, Iran e-mail: esieskandari123@gmail.com
NEDA AHANJIDEH*
Affiliation:
Department of Pure Mathematics, Faculty of Mathematical Sciences, Shahrekord University, P.O. Box 115, Shahrekord, Iran e-mail: ahanjidn@gmail.com
*
e-mail: ahanjideh.neda@sku.ac.ir
Get access Rights & Permissions [Opens in a new window]

Abstract

Assume that G is a finite group, N is a nontrivial normal subgroup of G and p is an odd prime. Let 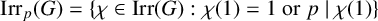$\mathrm{Irr}_p(G)=\{\chi \in \mathrm{Irr}(G) : \chi (1)=1~\mathrm{or}~ p \mid \chi (1)\}$ and 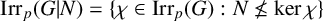$\mathrm{Irr}_p(G|N)=\{\chi \in \mathrm{Irr}_p(G) : N \not \leq \mathrm{ker}\,\chi \}$. The average character degree of irreducible characters of 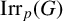$\mathrm{Irr}_p(G)$ and the average character degree of irreducible characters of 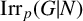$\mathrm{Irr}_p(G|N)$ are denoted by 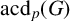$\mathrm{acd}_p(G)$ and 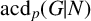$\mathrm{acd}_p(G|N)$, respectively. We show that if 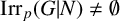$\mathrm{Irr}_p(G|N) \neq \emptyset $ and 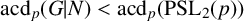$\mathrm{acd}_p(G|N) < \mathrm{acd}_p(\mathrm{PSL}_2(p))$, then G is p-solvable and 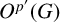$O^{p'}(G)$ is solvable. We find examples that make this bound best possible. Moreover, we see that if 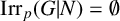$\mathrm{Irr}_p(G|N) = \emptyset $, then N is p-solvable and 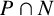$P \cap N$ and 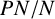$PN/N$ are abelian for every 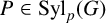$P \in \mathrm{Syl}_p(G)$.

Keywords

p-solvable groupaverage character degree

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20D05: Finite simple groups and their classification

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 3 , June 2024 , pp. 507 - 511
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahanjideh, N., ‘The average character degree and $r$ -solvability of a normal subgroup’, Monatsh. Math. 200 (2023), 487–493.CrossRefGoogle Scholar
Akhlaghi, Z., ‘On the average degree of linear and even degree characters of finite groups’, Ric. Mat. (to appear). Published online (14 November 2022).CrossRefGoogle Scholar
Akhlaghi, Z., ‘On the average degree of some irreducible characters of a finite group’, Math. Nachr. (to appear). Published online (8 March 2023).CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Moretó, A. and Nguyen, H. N., ‘On the average character degree of finite groups’, Bull. Lond. Math. Soc. 46(3) (2014), 454–462.CrossRefGoogle Scholar
Navarro, G. and Tiep, P. H., ‘Characters of relative ${p}^{\prime }$ -degree over normal subgroups’, Ann. of Math. (2) 178 (2013), 1135–1171.CrossRefGoogle Scholar
Nguyen, H. N. and Tiep, P. H., ‘The average character degree and an improvement of the Ito–Michler theorem’, J. Algebra 550 (2020), 86–107.Google Scholar
Qian, G., ‘On the average character degree and the average class size in finite groups’, J. Algebra 423 (2015), 1191–1212.CrossRefGoogle Scholar