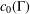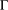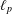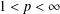Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Petitjean, C.
2017.
Lipschitz-free spaces and Schur properties.
Journal of Mathematical Analysis and Applications,
Vol. 453,
Issue. 2,
p.
894.
Avilés, Antonio
Martínez-Cervantes, Gonzalo
Rodríguez, José
and
Rueda Zoca, Abraham
2022.
Topological properties in tensor products of Banach spaces.
Journal of Functional Analysis,
Vol. 283,
Issue. 12,
p.
109688.
Chen, Dongyang
Kania, Tomasz
and
Ruan, Yingbin
2022.
On quantitative Gelfand-Phillips property and Phillips property.
Journal of Mathematical Analysis and Applications,
Vol. 516,
Issue. 2,
p.
126532.